
- •Теоретические основы информатики Расчетно-графическая работа №1
- •Теоретическая часть
- •Аддитивная (логарифмическая) мера (структурный подход).
- •Статистический подход к измерению информации.
- •Примеры решения задач
- •Задание
- •Содержание отчета
- •Варианты задания
- •Оформление ргр
- •Список литературы
- •Приложение 1
Теоретические основы информатики Расчетно-графическая работа №1
Тема: «Расчет количества информации по мерам Хартли и Шеннона».
Теоретическая часть
В информатике, как правило, измерению подвергается информация, представленная дискретным сигналом. При этом различают следующие подходы:
структурный подход. Измеряет количество информации простым подсчетом информационных элементов, составляющих сообщение. Применяется для оценки возможностей запоминающих устройств, объемов передаваемых сообщений, инструментов кодирования без учета статистических характеристик их эксплуатации.
статистический подход. Учитывает вероятность появления сообщений: более информативным считается то сообщение, которое менее вероятно, т.е. менее всего ожидалось. Применяется при оценке значимости получаемой информации.
семантический подход. Учитывает целесообразность и полезность информации. Применяется при оценке получаемой информации. Данный подход рассматривать не будем.
Аддитивная (логарифмическая) мера (структурный подход).
Эта мера предложена в 1928 году американским ученым Хартли, поэтому имеет второе название – мера Хартли. Хартли впервые ввел специальное обозначение для количества информации – I и предложил следующую логарифмическую зависимость между количеством информации и мощностью исходного алфавита:
I = l log2 h, (1)
где I – количество информации, содержащейся в сообщении;
l – длина сообщения;
h – мощность исходного алфавита;
Для k источников информации:
I= I1 +…+Ik. (2)
При исходном алфавите {0,1}; l = 1; h = 2 и, имеем
I = 1*log22 = 1. (3)
Формула (3) даёт аналитическое определение бита (BIT - BInary digiT) по Хартли: это количество информации, которое содержится в двоичной цифре.
Единицей измерения информации в аддитивной мере является бит.
Статистический подход к измерению информации.
В 30-х годах ХХ века американский ученый Клод Шеннон предложил связать количество информации, которое несет в себе некоторое сообщение, с вероятностью получения этого сообщения.
Вероятность p – количественная априорная (т.е. известная до проведения опыта) характеристика одного из исходов (событий) некоторого опыта. Измеряется в пределах от 0 до 1. Если заранее известны все исходы опыта, сумма их вероятностей равна 1, то сами исходы составляют полную группу событий. Если все исходы могут свершиться с одинаковой долей вероятности, они называются равновероятными.
Например, пусть опыт состоит в сдаче студентом экзамена по ТОИ. Очевидно, у этого опыта всего 4 исхода (по количеству возможных оценок, которые студент может получить на экзамене). Тогда эти исходы составляют полную группу событий, т.е. сумма их вероятностей равна 1. Если студент учился хорошо в течение семестра, значения вероятностей всех исходов могут быть такими:
p(5) = 0,5; p(4) = 0,3; p(3) = 0,1; p(2) = 0,1. (4)
Здесь запись p(j) означает вероятность исхода, когда получена оценка j (j = {2, 3, 4, 5}).
Если студент учился плохо, можно заранее оценить возможные исходы сдачи экзамена, т.е. задать вероятности исходов, например, следующим образом:
p(5) = 0,1; p(4) = 0,2; p(3) = 0,4; p(2) = 0,3. (5)
В![]() обоих случаях выполняется условие:
обоих случаях выполняется условие:
где n – число исходов опыта,
i – номер одного из исходов.
Пусть можно получить n сообщений по результатам некоторого опыта (т.е. у опыта есть n исходов), причем известны вероятности получения каждого сообщения (исхода) - pi. Тогда в соответствии с идеей Шеннона, количество информации I в сообщении i определяется по формуле (6):
I = -log2 pi, (6)
где pi – вероятность i-го сообщения (исхода).
Соотношение (6) позволяет определять также размер двоичного эффективного кода, требуемого для представления того или иного сообщения, имеющего определенную вероятность появления.
П
(7)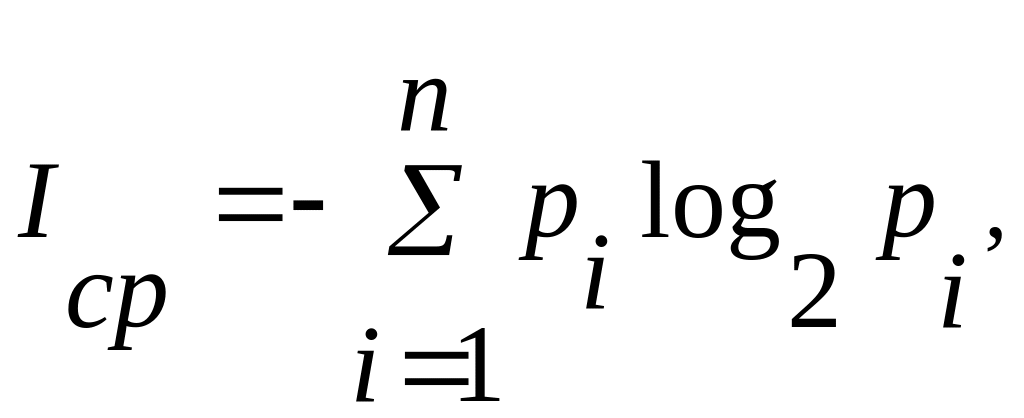
где pi – вероятность i-го сообщения.
На практике часто вместо вероятностей используются частоты исходов. Это возможно, если опыты проводились ранее и существует определенная статистика их исходов.
П![]() усть
источник передает элементарные
сигналы m различных
типов. Пусть в некотором отрезке сообщений
имеется N1
сигналов первого типа,
N2
сигналов
второго типа, ..., Nm
сигналов m
-го типа, причем
– общее число сигналов в наблюдаемом
отрезке. Тогда полное количество
информации, доставленное отрезком
из N сигналов,
будет равно:
усть
источник передает элементарные
сигналы m различных
типов. Пусть в некотором отрезке сообщений
имеется N1
сигналов первого типа,
N2
сигналов
второго типа, ..., Nm
сигналов m
-го типа, причем
– общее число сигналов в наблюдаемом
отрезке. Тогда полное количество
информации, доставленное отрезком
из N сигналов,
будет равно:
(8)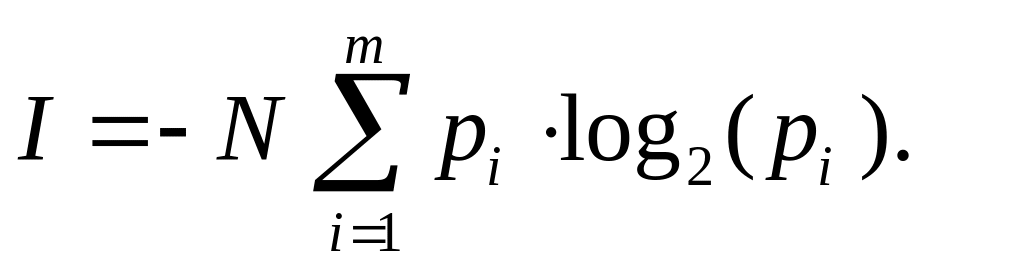
Пусть у опыта два равновероятных исхода, составляющих полную группу событий, т.е. p1 = p2 = 0,5. Тогда имеем в соответствии с (7):
I ср = -(0,5*log20,5 + 0,5*log20,5) = 1. (9)
Формула (9) есть аналитическое определение бита по Шеннону: это среднее количество информации, которое содержится в двух равновероятных исходах некоторого опыта, составляющих полную группу событий.
Формула, предложенная Хартли, представляет собой частный случай более общей формулы Шеннона. Если имеется N равновероятных исходов некоторого опыта, то от формулы (8) мы приходим к формуле (1)
Единица измерения информации при статистическом подходе – бит.
