Тема 2. Основы представления и обработки информации в компьютере Литература

1. Информатика в экономике: Учебное пособие/Под ред. Б.Е. Одинцова, А.Н. Романова. – М.: Вузовский учебник, 2008.

2. Информатика: Базовый курс: Учебное пособие/Под ред. С.В. Симоновича. – СПб.: Питер, 2009.

3. Информатика. Общий курс: Учебник/Соавт.:А.Н. Гуда, М.А. Бутакова, Н.М. Нечитайло, А.В. Чернов; Под общ. ред. В.И. Колесникова. – М.: Дашков и К, 2009.

4. Информатика для экономистов: Учебник/Под ред. Матюшка В.М. - М.: Инфра-М, 2006.

5. Экономическая информатика: Введение в экономический анализ информационных систем.- М.: ИНФРА-М, 2005.

1. Меры информации (синтаксическая, семантическая, прагматическая)

Для измерения информации могут применяться различные подходы, но наибольшее распространение получили статистический (вероятностный), семантический и прагматический методы.

Статистический (вероятностный) метод измерения информации был разработан К. Шенноном в 1948 году, который предложил количество информации рассматривать как меру неопределенности состояния системы, снимаемой в результате получения информации. Количественно выраженная неопределенность получила название энтропии. Если после получения некоторого сообщения наблюдатель приобрел дополнительную информацию о системе Х, то неопределенность уменьшилась. Дополнительно полученное количество информации определяется как:

,

где - дополнительное количество информации о системе Х, поступившее в форме сообщения;

- начальная неопределенность (энтропия) системы X;

- конечная неопределенность (энтропия) системы X, наступившая после получения сообщения.

Если система X может находиться в одном из дискретных состояний, количество которых n, а вероятность нахождения системы в каждом из них равна и сумма вероятностей всех состояний равна единице , то энтропия вычисляется по формуле Шеннона:

,

где - энтропия системы Х;

а - основание логарифма, определяющее единицу измерения информации;

n – количество состояний (значений), в котором может находится система.

Энтропия величина положительная, а так как вероятности всегда меньше единицы, а их логарифм отрицательный, поэтому знак минус в формуле К.Шеннона делает энтропию положительной. Таким образом, за меру количества информации принимается та же энтропия, но с обратным знаком.

Взаимосвязь информации и энтропии можно понимать следующим образом: получение информации (ее увеличение) одновременно означает уменьшение незнания или информационной неопределенности (энтропии)

Таким образом, статистический подход учитывает вероятность появления сообщений: более информативным считается то сообщение, которое менее вероятно, т.е. менее всего ожидалось. Количество информации достигает максимального значения, если события равновероятны.

Р. Хартли предложил следующую формулу для измерения информации:

I=log₂n ,

где n - количество равновероятных событий;

I – мера информации в сообщении о наступлении одного из n событий

Измерение информации выражается в ее объёме. Чаще всего это касается объёма компьютерной памяти и объёма данных, передаваемых по каналам связи. За единицу принято такое количество информации, при котором неопределённость уменьшается в два раза, такая единица информации получила название бит.

Если в качестве основания логарифма в формуле Хартли используется натуральный логарифм ( ), то единицей измерения информации является нат (1 бит = ln2 ≈ 0,693 нат). Если в качестве основания логарифма используется число 3, то - трит, если 10, то - дит (хартли).

На практике чаще применяется более крупная единица - байт (byte), равный восьми битам. Такая единица выбрана потому, что с ее помощью можно закодировать любой из 256 символов алфавита клавиатуры компьютера (256=2⁸).

Кроме байтов информация измеряется полусловами (2 байта), словами (4 байта) и двойными словами (8 байт). Широко используются также еще более крупные единицы измерения информации:

1 Килобайт (Кбайт - kilobyte) = 1024 байт = 2¹⁰ байт,

1 Мегабайт (Мбайт - megabyte) = 1024 Кбайт = 2²⁰ байт,

1 Гигабайт (Гбайт - gigabyte) = 1024 Мбайт = 2³⁰ байт.

1 Терабайт (Тбайт - terabyte) = 1024 Гбайт = 2⁴⁰ байт,

1 Петабайт (Пбайт - petabyte) = 1024 Тбайт = 2⁵⁰ байт.

В 1980 году российский математик Ю. Манин предложил идею построения квантового компьютера, в связи с чем появилась такая единица информации как кубит (quantum bit, qubit) – «квантовый бит» – мера измерения объема памяти в теоретически возможном виде компьютера, использующем квантовые носители, например - спины электронов. Кубит может принимать не два различных значения ("0" и "1"), а несколько, соответствующих нормированным комбинациям двух основных состояний спина, что дает большее число возможных сочетаний. Так, 32 кубита могут закодировать около 4 млрд состояний.

Семантический подход. Синтаксической меры не достаточно, если требуется определить не объем данных, а количество нужной в сообщении информации. В этом случае рассматривается семантический аспект, позволяющий определить содержательную сторону сведений.

Для измерения смыслового содержания информации можно воспользоваться тезаурусом ее получателя (потребителя). Идея тезаурусного метода была предложена Н. Винером и развита нашим отечественным ученым А.Ю. Шрейдером.

Тезаурусом называется совокупность сведений, которыми располагает получатель информации. Соотнесение тезауруса с содержанием поступившего сообщения позволяет выяснить, насколько оно снижает неопределенность..

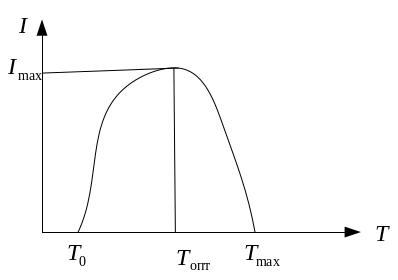
Зависимость объема смысловой информации сообщения от тезауруса получателя

Согласно зависимости, представленной на графике, при отсутствии у пользователя какого-либо тезауруса (знаний о существе поступившего сообщении, то есть =0), или наличия такого тезауруса, который не изменился в результате поступления сообщения ( ), то объем семантической информации в нем равен нулю. Оптимальным будет такой тезаурус ( ), при котором объем семантической информации будет максимальным ( ). Например, семантической информации в поступившем сообщении на незнакомом иностранном языке будет ноль, но и такая же ситуация будет в том случае, если сообщение уже не является новостью, так как пользователю уже все известно.

Прагматическая мера информации определяет ее полезность в достижении потребителем своих целей. Для этого достаточно определить вероятность достижения цели до, и после получения сообщения и сравнить их. Ценность информации (по А.А. Харкевичу) рассчитывается по формуле:

,

где - вероятность достижения цели до получения сообщения;

- вероятность достижения цели поле получения сообщения;