Исчисление предикатов

В исчислении предикатов, так же как и в исчислении высказываний, на первом по важности месте стоит проблема разрешимости.

Но в исчислении высказываний проблема разрешимости состояла в решении вопроса является ли данная сложная функция тождественно истинной, выполнимой или тождественно ложной?

Теперь же вопрос ставится иначе. Принимает ли данная функция значение 1 при:

а) любых предметных переменных и любых предикатах,

б) на некотором множестве предметных переменных и любых преди­катах,

в) при некоторых значениях предметных переменных и при некото­рых предикатах,

г) является ли она тождественно ложной, т. е. невыполнимой?

Таким образом, в логике предикатов, в отличие от логики высказыва­ний, нет эффективного способа для распознавания общезначимости функ­ций.

Поэтому в исчислении предикатов указывается некоторая совокуп­ность формул, которые называются аксиомами и составляют аксиомати­ческую теорию, и указывается конечное множество отношений между формулами, составляющее правила вывода.

Аксиоматическая теория и правила вывода составляют исчисления предикатов.

Символами исчисления предикатов или алфавитом исчисления пре­дикатов являются символы предметных переменных, символы предика­тов, логические символы (отрицание и импликация), символы кванторов, а также скобки и запятая.

Сформулируем аксиомы исчисления предикатов и правила вывода исчисления предикатов.

Аксиомы исчисления предиката.

Пусть А, В и С - любые формулы.

Аксиома 1. А→ (В →А).

Аксиома 2. (А → (В → С)) → ((А → В) → (А → С)).

Аксиома 3. (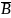 → 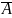) →(( → А) → В).

Аксиома 4. ( х_i)А(х_i) → А(х_i), где формула А(х_i) не содержит перемен­ной x_i.

Аксиома 5. A(x_i) → ( x_j)A(x_j), где формула А(x_i) не содержит перемен­ной x_j.

Правила вывода исчисления предикатов.

(1) Пусть (А(х) → В) и В не содержит переменной х, тогда

(((( x)А(х)) → В) .

Это правило связывания квантором существования.

(2) Пусть В → А(х) и В не содержит переменной х, тогда

(В → (( х)A(x))).

Это правило связывания квантором общности.

(3) Связанную переменную формулы В можно заменить другой пе­ременной, не являющейся свободной в В. Это правило переименования связанной переменной.

Практическое занятие по теме «Предикаты»

Задача 1. Пусть U - множество всех действительных чисел. Постройте множе­ство истинности для каждого из следующих предикатов:

а) х² - 4 = 0, б) х² + 4 = 0, в) х² - 4х + 3 = 0, г) х² - 4х + 4 = 0, д) х² - 4х + 5 = 0.

Ответ: а) {2, -2}, б) , В) {3, 1}, г) {2}, д) .

Задача 2. Пусть U - множество всех действительных чисел. Найдите множество истинности конъюнкций следующих предикатов:

а) х² + х - 2 = о; х² = 4, б) х² - 4 = о; х² - 4х + 4 = 0,

в) х³ - 6х² + 11х - 6 = 0; х² - 4х + 3 = о, г) х³ = 1; х² - 4х + 4 = 0.

Задача 3. На множестве однозначных натуральных чисел даны два предиката: предикат Р(х): «число 3 делитель х»; предикат Q(x): «х ≤ 6,). Найдите множества истинности предикатов:

(1) Р(х) ˅ Q(x), (2) Р(х) ˄ 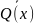, (3) 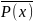→ Q(x), (4) .

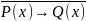Решение. (1) {1, 2, 3, 4, 5, 6, 9}, (2) {9}, (3) {1, 2, 3, 4,5,6, 9}, (4) {9}.

Задача 4.

Предикат Р(х): « х есть простое число»;

предикат Q(x): «х есть действи­тельное число»;

предикат Т(х): «х меньше y».

Запишите следующие утвержде­ния, используя кванторы:

а) каждое рациональное число есть действительное число;

б) существует число, которое является простым;

в) для каждого числа х существует такое число y, что х < у.

Решение.

а) ( x) (Q(x) ↔R(x));

б) ( х)Р(х);

в) (( x)( ( y)T(x)).