4.7. Расчет ригеля по наклонному сечению (подбор поперечной арматуры)
В курсовом проекте расчет ригеля по наклонному сечению не производим. Поперечную арматуру принимаем только по конструктивным требованиям.
Диаметр поперечной арматуры принимаем из условия сварки с продольной рабочей арматурой.
Для продольной рабочей арматуры ø25A500 принимаем поперечную арматуру ø10A-400.
Шаг поперечной арматуры:
- в близи опор (1/4 lo) шаг будет равен:
см;
принимаем шаг 20см;
- в средней части плиты шаг будет равен:
см;
принимаем шаг 25см.
Проверяем, требуется ли поперечная арматура по расчёту, из условия:
Q ≤Q b,min = 0,5 R bt bh 01, (2)
т.е. Q=154,1 кН > Qb,min=0,5×0,9×0,14×30×35=66,15 кН,
поэтому расчёт поперечной арматуры необходим.
Q
- поперечная
сила в наклонном сечении с длиной
проекции с от внешних сил, расположенных
по одну сторону от рассматриваемого
наклонного сечения; при вертикальной
нагрузке, приложенной к верхней грани
элемента, значение Q
принимается
в нормальном сечении, проходящем на
расстоянии с
от
опоры.
Qb - поперечная сила, воспринимаемая бетоном в наклонном сечении.
Qsw - поперечная сила, воспринимаемая хомутами в наклонном сечении. По ф. (3.45),(3.46) [2]
В соответствии с
п. 5.21 [2] максимальный шаг хомутов не
должен превышать 300 мм.
Примем в первом приближении sw = 20 см. Для хомутов примем арматуру класса А400 (Rsw=285 МПа) диаметром 10 мм (As=0.785 см2). В соответствии с п. 3.32 и ф. (3.48) [2]
Очевидно, что условие для опорных участков ригеля соблюдается с ещё большим запасом.
При действии на ригель равномерно распределённой нагрузки q=g1+v1 длина участка с интенсивностью усилия в хомутах q sw,1 принимается не менее значения l1
Qb,min=0,5×0,9×0,14×30×35=66,15 кН
Принимаем
с=80;
кН/м.=0,51кН/см
Ns=
Nw=
бsAs= Nw+ Ns=11.1+42.34=53.44кН
Определим высоту сжатой зоны бетоны (без учёта сжатой арматуры):
Х=
Невыгоднейшее значение «с»:
Расчётный момент M в сечении, проходящем через конец наклонного сечения, равен:
М= Q(a0+ W0)-0,5q(а0+W0)2=154.1(8.5+97.55)-0.5*0.5061(8.5+97.55)2=13496.35кНсм=134,96кНм
Проверим условие:
М=134,96<53,44*37+0,5*2,24*92,552=14570,64кНсм=145,7кНм
Условия прочности соблюдаются.
4.8. Построение эпюры материалов (нахождение точки теоретического обрыва стержней)
Для построения эпюры материалов необходимо в первую очередь построить эпюру моментов, возникающих ригеле и нанести на нее максимальное и промежуточные значения моментов. Промежуточные значения величин моментов определяем по формулам:
;
;
,
где Q – поперечная сила; Q = 154,1 кН;
lo – расчетная длина ригеля; lo = 6,09м;
q – полная распределенная нагрузка на ригель; q = 50,61кН/м;
кН∙м;
кН∙м;
кН∙м.
Определим фактическое усилие, которое сечение ригеля может выдержать. Для этого найдем значение ξ по формуле:
,
где
– фактическая площадь рабочей арматуры;
для 4ø25A500
= 19,64см2;
Rs – расчетное сопротивление арматуры; Rs = 520МПа;
b – ширина ригеля поверху; b = 30см;
ho – расстояние от оси арматуры до верха ригеля (рабочая высота); ho = 35см;
γb1 – коэффициент, учитывающий длительность нагрузки; γb1 = 0,9;
Rb – расчетное сопротивление бетона; Rb = 22МПа;
.
По приложению 10 находим значение ζ, соответствующее найденному значению ξ = 0,41 (или ближайшему по величине к найденному). Для ξ = 0,41 значения этой величины будет равно ζ = 0,795.
Максимальный момент, воспринимаемый сечением, определяется по формуле:
;
Т.к. изгибающий момент в ригеле не постоянен (уменьшается к краям), то ближе к раю ригеля сечение будет недогружено (будет перерасход арматуры). Следовательно, часть рабочей арматуры можно до конца не доводить. Т.к. арматура принята одинаковой, то не доводим до конца верхние стержни рабочей арматуры. В данном сечении фактическая площадь будет равна = 9,82см2. Расстояние от оси арматуры до верха ригеля (рабочая высота) будет равна h01 = 37см (рис.4.4).
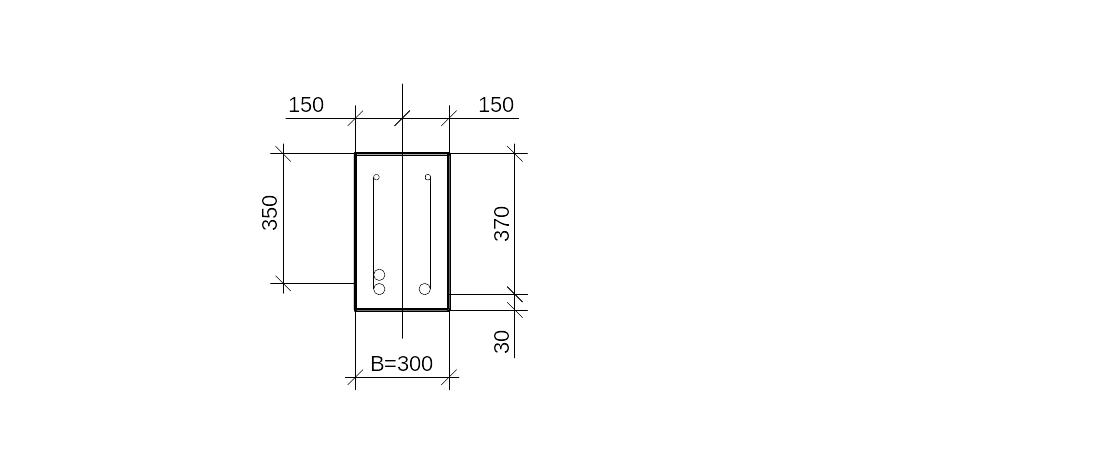
Рис. 4.4. К определению усилий, воспринимаемых сечением.
Для этого сечения найдем значение ξ по формуле:
,
.
По приложению 10 находим значение ζ, соответствующее найденному значению ξ = 0,19 (или ближайшему по величине к найденному). Для ξ = 0,19 значения этой величины будет равно ζ = 0,905.
Максимальный момент, воспринимаемый данным сечением (с двумя стержнями арматуры), определяется по формуле:
;
кН∙м.
Рис. 4.5. Эпюра материалов.
Значения максимальных моментов М4 и М2 наносим на эпюру материалов. В точках пересечения линии М2 и эпюры моментов М верхние стержни будут обрываться. Но для работы верхних стержней необходима их дополнительная заделка с каждой стороны на величину W, равную 20 диаметрам арматуры:
Места теоретического обрыва арматуры можно определить аналитически.
M=143кН.
M=
145x-25,305х
=143
х1=1,27 м
х2=4,465 м
Это точки теоретического обрыва арматуры.
Длина обрываемого стержня будет равна 4,465-1,27+2*0,3=3,8 м
Принимаем длину обрываемого стержня 4м.
Определяем аналитически величину поперечной силы в месте теоретического обрыва арматуры х=0,97м
Графически поперечная сила была принята
95,27 кН с достаточной степенью точности.