Лабораторная работа № 9

ИССЛЕДОВАНИЕ ИНДУКЦИИ МАГНИТНОГО ПОЛЯ НА ОСИ СОЛЕНОИДА

Цель работы: исследование индукции магнитного поля на оси соленоида.

Приборы и принадлежности: лабораторный комплекс ЛКЭ-1 «Электромагнитное поле», имеющий генератор сигналов функциональный ГСФ-1, осцил­лограф тип С1-131/1, два соленоида, датчик эталонный на рейтере, магазин сопротив­лений.

Теоретическое введение

С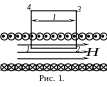 оленоид представляет собой изолированный провод, навитый плотно, виток к витку, на цилиндрический каркас. При исследовании магнитных ха­рактеристик различ­ных веществ с использованием соленоида, необходимо знать значение напряженности магнитного поля на его оси. Напряжен­ность характеризует магнитное поле, создан­ное токами проводимости и не зависящие от магнитных свойств, присутствую­щего вещества.

Магнитное поле длинного соленоида (длина его много больше диаметра витков) можно рассчитать, используя теорему о циркуляции вектора . Со­гласно этой теореме циркуляция вектора по произвольному контуру равна алгебраической сумме макро­токов, охватываемых этим контуром:

(1)

Внутри длинного соленоида поле однородное, а вне его - неоднородное и очень слабое. Возьмем прямоугольный контур 1-2-3-4-1, охватывающий витков соле­ноида (рис.1). Циркуляция по этому замкнутому контуру равна:

(2)

Второй и четвертый интегралы правой части равны нулю, так как вектор перпендикуля­рен к участкам контура, по которым они берутся. Взяв уча­сток 3-4 на большом рас­стоянии от соленоида (где поле заведомо должно быть очень слабым), третьим слагае­мым можно пренебречь. Следовательно,

где - напряженность поля в тех точках, где располагается отрезок 1-2, -длина этого отрезка.

Согласно (1)

.

Отсюда

,

где число витков, приходящееся на единицу длины соленоида.

Наряду с напряженностью вводится другая векторная характеристика магнитного поля – магнитная индукция . Индукция и напряженность магнитного поля связаны соотношением

,

где - магнитная проницаемость вещества (для воздуха ); - магнитная постоянная.

C учетом этого получим формулу для определения индукции магнитного поля на оси соленоида (внутри его):

.

Н а практике, как правило, используют соленоиды, отношение длины ко­торых к их диаметру лежит в пределах от 5 до 10. В случае однослойного такого соленоида, напря­женность магнитного поля в любой точке А, лежащей на его оси , направлена вдоль оси по правилу буравчика и численно равна алгебраической сумме напряженностей магнитных полей, создаваемых в любой точке А всеми витками (рис.2). Индукция В маг­нитного поля в произвольной точке А оси соленоида численно равна

, (3)

где - сила тока в амперах; - число витков соленоида на 1 м длины; и - углы, которые образуют с осью соленоида радиус – векторы и , про­веденные из точки А к крайним виткам соленоида.

При многослойной обмотке соленоида поле в точках наблюдения явля­ется результа­том наложения полей отдельных слоев, каждое из которых рассчитывается по формуле (3). Поэтому, качественно, поле многослойного соленоида имеет такой же вид, как и поле од­нослойного.

Однако расчет по формуле (3) поля многослойного соленоида громоздок и не обеспе­чивает требуемой точности, так как в процессе его намотки трудно обеспечить идеаль­ное прилегание витков соседних слоев. Поэтому напряженность магнитного поля на оси многослойного соленоида опреде­ляют экспериментально.