§9. Емкости p-n перехода.

p-n переход обладает инерционностью, проявляющейся в том, что при мгновенном изменении тока через переход (выводы кристалла), напряжение на p-n переходе изменяется не мгновенно, т.е. нарушается соответствие между U и I, описываемое статической вольтамперной характеристикой:

.

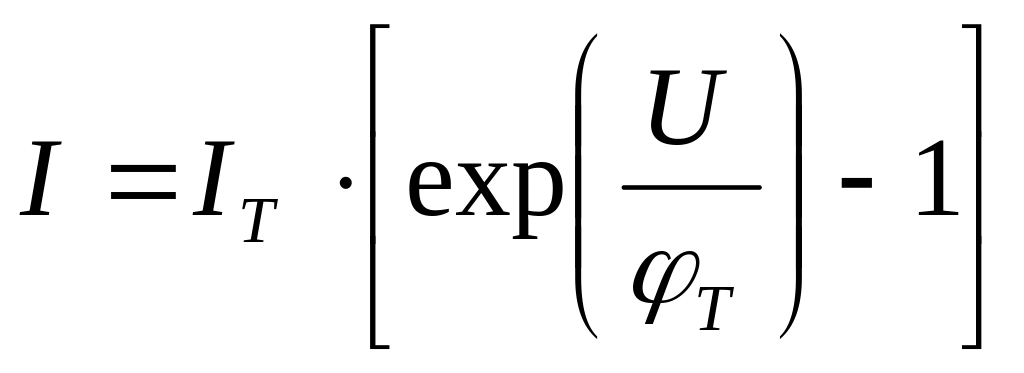В этом случае говорят, что p-n переход обладает емкостью.

Природа емкости p-n перехода двоякая и поэтому различают 2 емкости: барьерную (зарядовую) и диффузионную. Напомним, что емкость определяется как

,

Где Q – заряд, т.е. можно говорить о емкости электронного прибора, если в нем имеется заряд, зависящий от напряжения.

Барьерная емкость p-n перехода связана с зарядами неподвижных ионов в обедненной области полупроводника. Если растет , т.е. растет потенциальный барьер , то растет обедненная область , увеличивается количество положительных и отрицательных ионов, т.е. увеличивается Q. Характер зависимости Q от U определяется типом p-n перехода. Различают:

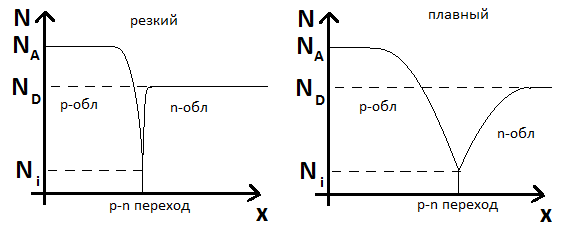
• резкие переходы – для которых характерно резкое изменение концентрации примесей при подходе к p-n переходу и

• плавные переходы – когда концентрация примесей изменяется плавно при подходе к p-n переходу.

Из курса физики вам известно, что вектор напряженности электростатического поля по величине равен, а по направлению противоположен градиенту электростатического потенциала или для одномерного случая .

Известно также, что согласно одному из уравнений Максвелла, расхождение вектора электрической индукции пропорционально плотности эклектического заряда или для одномерного случая . Объединение приведенных выше двух уравнений позволяет связать распределение потенциалов и концентрацию примесей, определяющих плотность пространственного заряда в p-n переходе. Уравнение имеет вид:

, -диэлектрическая проницаемость

и называется уравнением Пуассона.

Проинтегрировав дважды это уравнение, получим связь между разностью потенциалов на переходе и шириной обедненной области и концентрацией примесей.

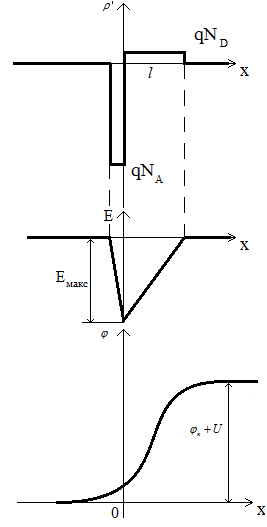
Рассмотрим резкий переход, у которого .

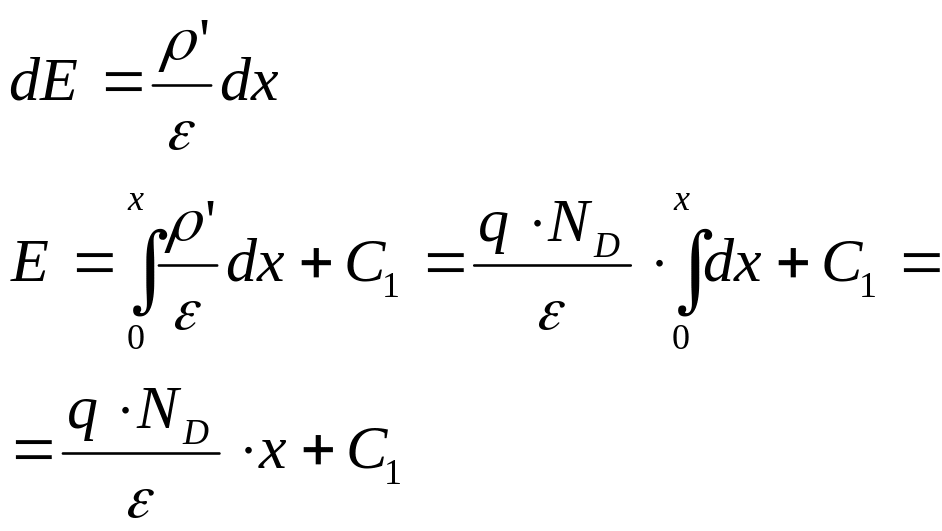
При x = E(x) = 0, поэтому

, откуда и .

Найдем распределение потенциала:

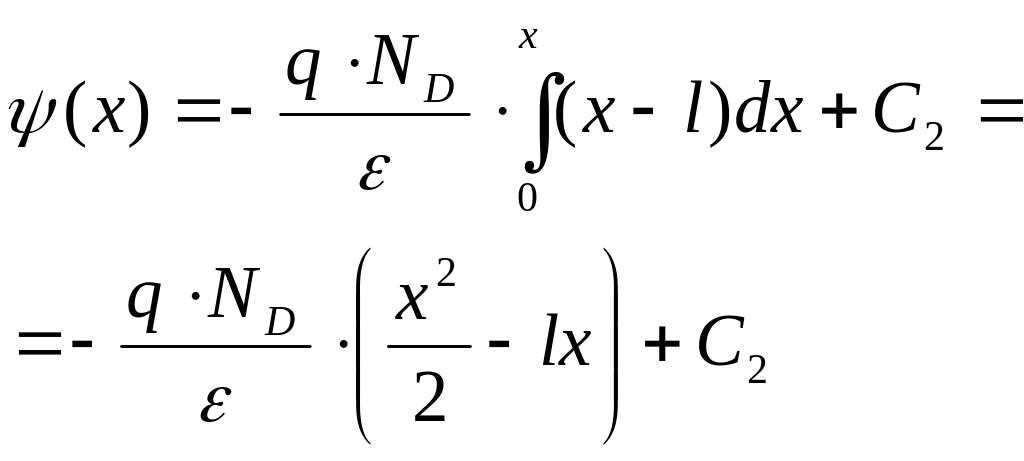
При x = ,

=> . Откуда .

Величина пространственного заряда, сосредоточенного в обедненной области толщиной l, составляет

, здесь S – площадь p-n перехода.

Откуда

.

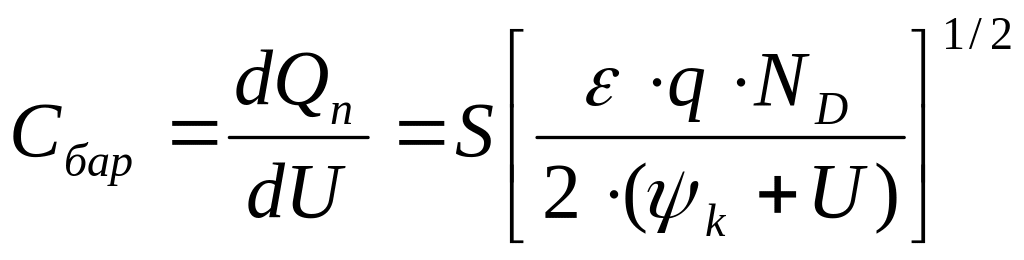Т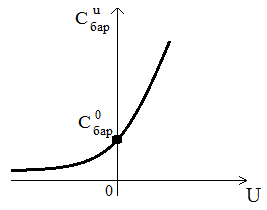 аким образом, барьерная емкость резкого p-n перехода обратно пропорциональна корню квадратному из напряжения, приложенного к p-n переходу.

для обратных напряжений.

Р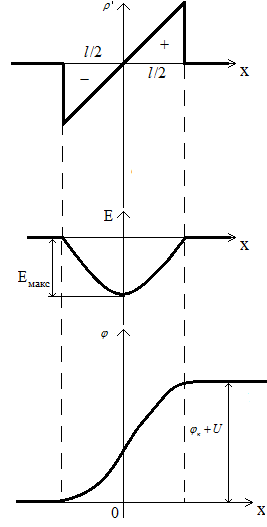 ассмотрим плавный p-n переход.

.

При x = E(x) = 0, поэтому

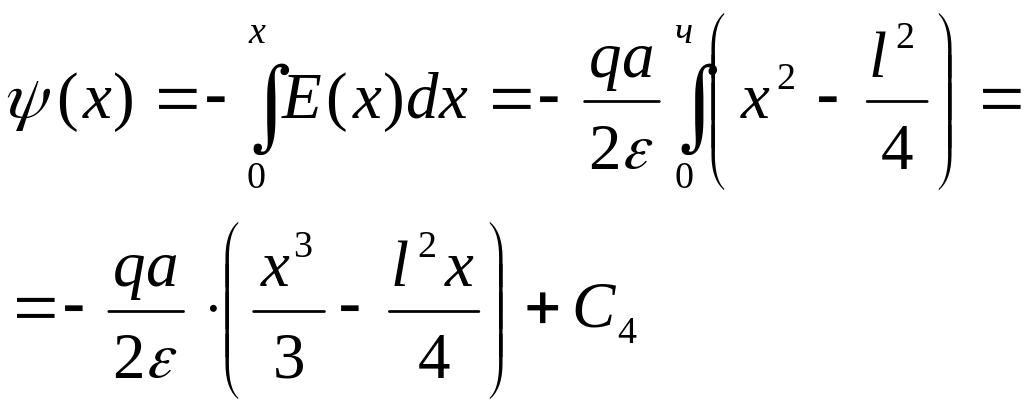
При x = 0 .

При x =

.

Пространственный заряд

Таким образом, емкость плавного перехода обратно пропорциональна кубическому корню из напряжения на переходе.

. .

Емкость резкого перехода определяется величиной концентрации примесей, а емкость плавного перехода определяется градиентом концентрации примесей в области объемного заряда.

Таким образом, зарядовую емкость p-n перехода можно отождествить с емкостью плоского конденсатора, у которого расстояние между пластинами равно l, а площадь пластин равна площади p-n перехода. Зарядная (барьерная) емкость тем больше, чем больше концентрация примесей на границе области объемного заряда и чем меньше напряжение на переходе.

Диффузионная емкость. Она связана с зарядом подвижных носителей заряда – электронов и дырок.

Показать наличие такой емкости можно на основе уравнения непрерывности. Рассматриваем открытый p-n переход, . Диффузионный ток – это дырок из p-области в n-область и электронов из n-области в p-область. Поскольку , то можно пренебречь электронными токами и рассматривать только инжекцию дырок в n-область. Эти инжектированные дырки и создают заряд , который приводит к появлению .

Решив уравнение непрерывности, мы получим распределение избыточной концентрации неосновных носителей заряда (дырок в n-области) вдоль координаты x.

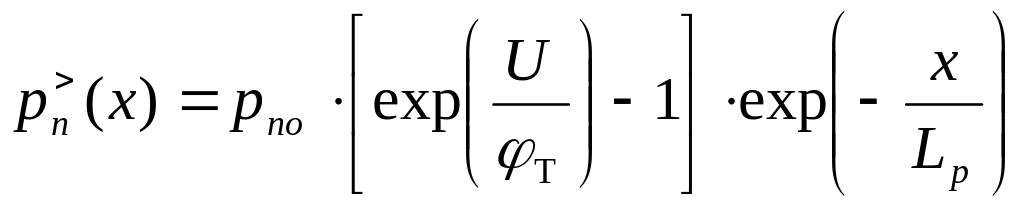
Учитывая, что пропорционально количеству избыточных неосновных носителей заряда в области базы (U-обл), найдем его, проинтегрировав выражение в пределах от 0 до ∞ (считаем, что ширина базы ):

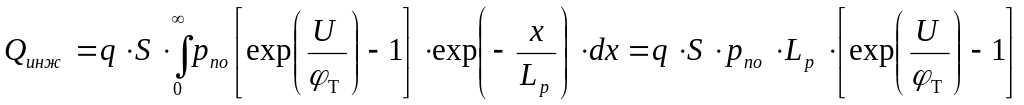
Домножим полученное выражение на отношение и учтем, что . Получим:

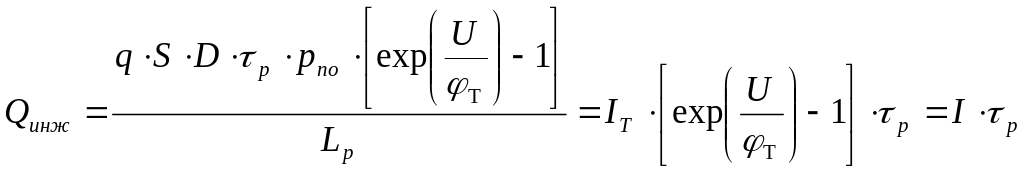
Далее,

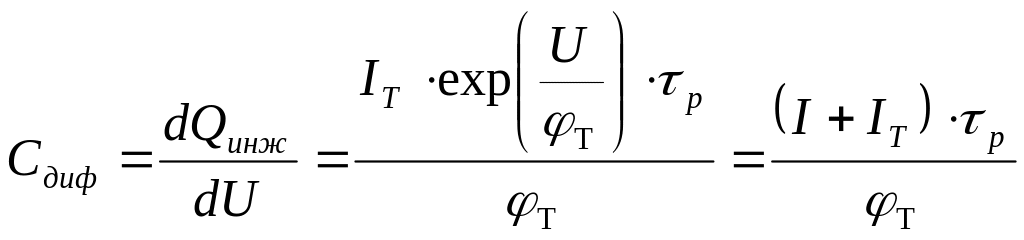
С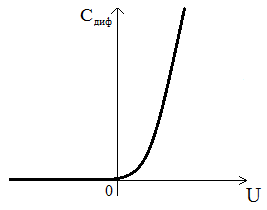 ледовательно, диффузионная емкость пропорциональна времени жизни носителей заряда и диффузионному току перехода обратно пропорциональна температурному коэффициенту. экспоненциально зависит от приложенного к p-n переходу напряжения U.

Следует отметить, что заряд не меняет электрической нейтральности базы, так как практически мгновенно через внешний вывод в базу приходит компенсирующий заряд электронов. Однако заряд существует и исчезнуть может, только если прекратить инжекцию через p-n переход (I = 0). Тогда заряд исчезнет с постоянной времени путем рекомбинации.

Выводы:

1. При U < 0 (обратное смещение p-n перехода) 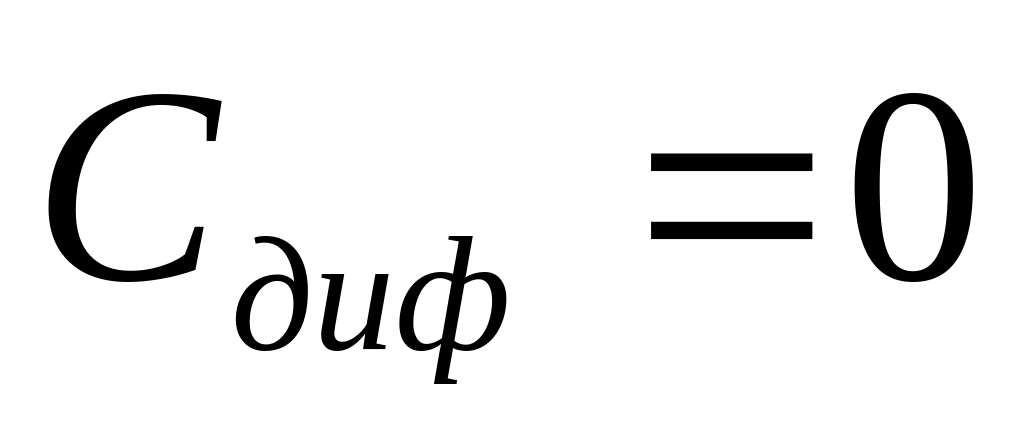и существует у p-n перехода только 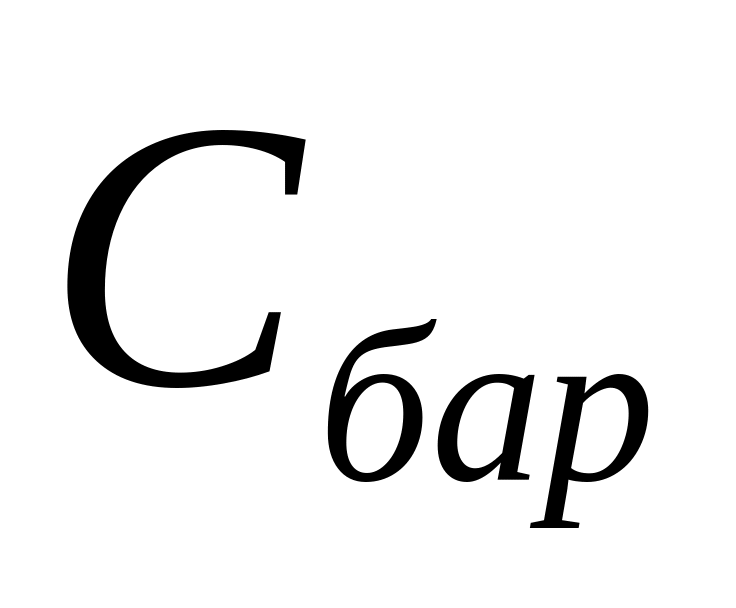. У современных транзисторных переходов составляет несколько пФ.

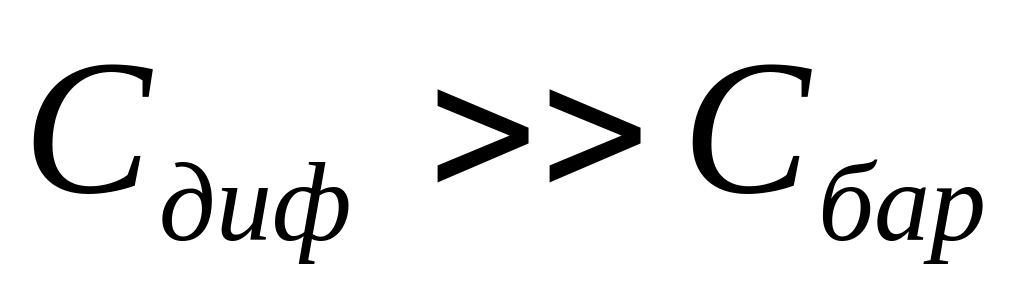2. При U > 0 (прямое смещение p-n перехода) , т.к. , и составляет десятки тысяч пФ.

Именно наличие емкостей у p-n переходов ограничивает скорости переключения и диапазоны усилительных частот в полупроводниковых приборах.