Суммирование систематических и случайных погрешностей

При проведении многократных измерений случайная погреш­ность может быть уменьшена во много раз. Однако погрешность усредненного результата будет определяться не этой весьма малой случайной погрешностью, а не зависящей от числа усредняющих отсчетов систематической погрешностью.

Механизм суммирования систематической и случайной состав­ляющих погрешности отличается от механизма суммирования слу­чайных погрешностей. Согласно ГОСТ 8.207—76 погрешность ре­зультата измерения определяется по следующим правилам. Если границы неисключенной систематической погрешности и оценка СКО результата измерения S связаны соотношением

< 0,8S (16)

то следует пренебречь систематической составляющей погрешнос­ти и учитывать только случайную погрешность результата. При этом доверительные границы погрешности результата А = t_pS, где t_p — коэффициент Стьюдента, зависящий от доверительной веро­ятности Р и числа проведенных измерений п. Если же имеет место неравенство

> 8S, (17)

то, наоборот, следует пренебречь случайной составляющей и резуль­тат характеризовать лишь границами его суммарной систематичес­кой погрешности А = 9. Погрешность, возникающая из-за пренебре­жения одной из составляющих погрешности, при выполнении указанных неравенств не превышает 15%.

Числа 0,8 и 8 в стандарте никак не обосновываются. Однако если принять во внимание, что, как было показано ранее, = 1,6S то условие (16) эквивалентно неравенству . Условие (17) эквивалентно неравенству . Следовательно, ГОСТ 8.207-76 разрешает пренебрегать систематической составляющей и учиты­вать только случайную составляющую лишь тогда, когда она в 2 раза превышает систематическую. Если же случайная составляю­щая менее 1/5 систематической, ею можно пренебречь.

При невыполнении неравенств (16) и (17) границу суммарной погрешности ГОСТ 8.207-76 предписывает находить путем компози­ции распределений случайных и неисключенных систематических пог­решностей, рассматриваемых как случайные величины. Допускается границы погрешности результата измерений определять по формуле

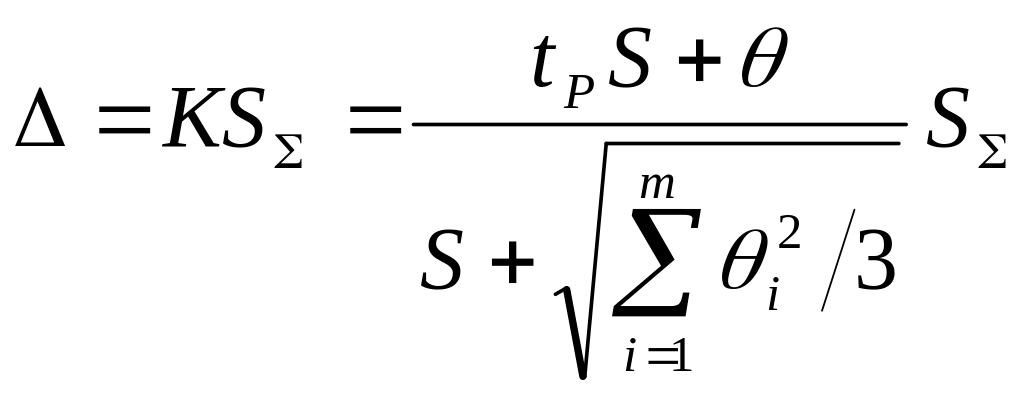
где - оценка суммарного СКО суммарной по-

грешности.

Данный подход, приводящий к заниженным оценкам, вызыва­ет [4] справедливые нарекания и вряд ли его следует считать правомочным. Рассмотрим этот вопрос подробнее.

Систематическая погрешность, присутствующая во всех отсчетах, не усредняется при статистической обработке. На рис. 1 показаны истин­ное значение измеряемой величины х_и, границы систематической по­грешности 6, распределение случайной составляющей погрешности р(х). Из рисунка ясен механизм суммирования составляющих погрешности. Если систематическая составляющая постоянна, то ее модуль | | дол­жен суммироваться с доверительным интервалом случайной состав­ляющей t_pS, а отнюдь не с СКО. Доверительный интервал суммарной погрешности = 2(| | + t_PS).

Из рис. 9.1 становятся понятными рассмотренные выше условия, при которых можно пренебречь одной из составляющих суммарной погрешности. На рис. 1,а показана ситуация, когда нельзя пренеб­речь ни одной из составляющих. На рис.1,б доверительный интер­вал случайной составляющей более чем в два раза больше системати­ческой составляющей, и последней можно пренебречь. На рис. 1,в

интер­вал случайной составляющей более чем в 5 раз, и ее также можно не учитывать при определении суммарной погрешности