1.1.3. Запись решения в mathcad :

Рис 1.1 – решение СЛАУ в Mathcad методом Гаусса.

1.2. Решение слау средствами матричного исчисления.

1.2.1. Теоретические сведения.

Матричный метод решения систем линейных алгебраических уравнений с ненулевым определителем состоит в следующем.

Пусть дана система линейных уравнений с n неизвестными (над произвольным полем):

Её можно переписать в матричной форме AX=B, где A — основная матрица системы, B и X — столбцы свободных членов и решений системы соответственно:

, , .

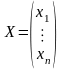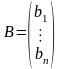Умножим это матричное уравнение слева на A^-1 — матрицу, обратную к матрицеA:

A^-1(AX) = A^-1∙B

Так как A∙A^-1 = E, получаем X = A^-1∙B . Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы А. Необходимым и достаточным условием этого является неравенство нулю определителя матрицы А:

det A ≠ 0

1.2.2. Произведение расчетов вручную.

Сначала проверим, не равен ли определитель матрицы коэффициентов СЛАУ нулю:

Для нахождения обратной матрицы необходимо вычислить алгебраические дополнения для всех элементов матрицы коэффициентов при переменных:

Далее найдём обратную матрицу:

Чтобы найти неизвестные, перемножим обратную матрицу на матрицу векторов свободных членов:

Итоговое решение системы: x₁ = 2; x₂ = -1; x₃ = 3.

1.2.3. Запись решения в mathcad.

Рис 1.2 - решение СЛАУ в Mathcad матричным методом.

2. Определение суммы, разности и произведения комплексных чисел.

Определить сумму, разность, произведение и частное комплексных чисел z₁и z₂, z₃ и z₄. Ответы представить в алгебраической и показательной формах комплексного числа.

2.1 Теоретические сведения.

Комплексным числом называется упорядоченная пара(a, b) действительных чисел. Поле комплексных чисел можно понимать как расширение поля вещественных чисел, в котором многочлен z²+1 имеет корень.

Действия над комплексными числами:

1. Сложение :

2. Вычитание :

3. Умножение :

4. Деление :

Алгебраическая форма записи комплексного числа имеет вид , гдеa, b— действительные числа, j— мнимая единица, для которой Числоaназывается действительной частью комплексного числа и обозначаетсяa = Rez, b = Imz — мнимая часть числа.

Сумма и произведение комплексных чисел могут быть вычислены непосредственным суммированием и перемножением таких выражений, как обычно раскрывая скобки и приводя подобные, чтобы представить результат тоже в стандартной форме (при этом надо учесть, что ).

Показательная форма записи комплексного числа имеет вид , где —формула Эйлера. — расширение экспоненты для случая комплексного показателя степени.

Отсюда вытекают следующие широко используемые равенства:

, .

Модулем (абсолютной величиной) комплексного числа называется длина радиус-вектора соответствующей точки комплексной плоскости (или, то же, расстояние между точкой комплексной плоскости, соответствующей этому числу, и началом координат). Модуль комплексного числа z (записывается |z|) определяется выражением:

Угол (в радианах) радиус-вектора точки, соответствующей числу z, называется аргументом числаz и обозначаетсяargz.

Из этого определения следует, что

2.2 Представление комплексных чисел в алгебраической форме:

2.3 Представление комплексных чисел в показательной форме:

2.4 Запись решения в MATHCAD.

Рис 2.1 – выполнение действий над комплексными числами в Mathcad.

3. Изображение векторов на комплексной плоскости.

На комплексной плоскости изобразить векторыZ₁, Z₂, Z₃, Z₄.Изобразить векторную сумму Z₁и Z₂, Z₃ и Z₄.

3.1. Теоретические сведения.

Пусть на плоскости введена ПДСК, тогда каждую точку плоскости можно отождествить с упорядоченной парой действительных чисел, которые являются ее координатами:

С другой стороны, каждое комплексное число можно также отождествить с упорядоченной парой действительных чисел , где — действительная часть комплексного числа z, — мнимая часть комплексного числа z.

Отсюда выводим, что каждое комплексное число можно отождествить с точкой координатной плоскости.

Координатная плоскость, каждая точка которой отождествлена с комплексным числом, называется комплексной плоскостью. Ось абсцисс Ох называется действительной осью. Ось ординат Оу называется мнимой осью.

Существует взаимно однозначное соответствие между точками координатной плоскости и их радиус-векторами. Поэтому также существуют взаимно однозначное соответствие и между всеми комплексными числами и радиус-векторами соответствующих точек комплексной плоскости.

Итак, чтобы изобразить комплексное число zточкой на комплексной плоскости нужно записать его в алгебраической форме записи, найти его действительную и мнимую части и построить в ПДСК на этой плоскости точку, абсцисса которой равна действительной части, а ордината —мнимой части данного комплексного числа z:

_,

где вектор Ozявляется радиус-вектором точки z.

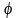Введем на комплексной плоскости полярную систему координат стандартным образом совмещенную с ПДСК, т.е. с полюсом в начале координат и полярным лучом, совмещенным с положительной полуосью абсцисс. Тогда точка zимеет полярные координаты где r— полярный радиус точки z, а — её полярный угол.

При такой геометрической интерпретации комплексного числа как точки на комплексной плоскости ее полярные координаты, как и декартовые, получили специальные названия и обозначения.

Модулем комплексного числа называется полярный радиус точки комплексной плоскости отождествленной с этим числом.

Аргументом комплексного числа называетсяполярныйугол точки комплексной плоскости отождествленной с этим числом.

Таким образом, полярными координатами точки zкомплексной плоскости являются модуль и аргумент комплексного числа z:

Из определений следует, что

Можно дать такое определение модуля комплексного числа, совпадающее с первым.

Модулем комплексного числа называется расстояние от начала координат комплексной плоскости до точки, отождествленной с этим числом.

Так как действительные числа изображаются здесь точками на координатной оси Ох, то данное выше определение модулякомплексного числа является одновременно и определением модуля действительного числа.

Модулем действительного числа называется расстояние от начала координат до точки числовой оси, отождествленной с этим числом, действительного числа называется расстояние от начала координат до точки числовой оси, отождествленной с этим числом.