§ 5. Выборочные оценки параметров системы двух случайных величин
При статистическом анализе системы двух случайных величин каждый элемент выборки характеризуется парой чисел - значением случайной величины Х и значением случайной величины Y. Т.е. выборка объема n - это последовательность пар чисел
(6.5.1)
Оценки параметров каждой из величин находятся по формулам (4.3.5) - (4.3.10), например,
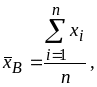
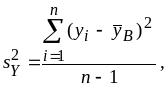и т.д.
Оценка коэффициента корреляции - выборочный коэффициент корреляции - определяется по формуле
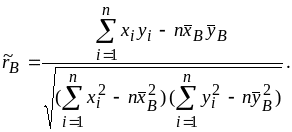(6.5.2)
Среди пар в выборке (6.5.1) могут быть и одинаковые, поэтому при достаточно больших объемах выборки бывает удобно выборку представить в виде табл.8.
Таблица 8
В табл.8 приведены
все k
различных пар в выборке.
-
это частота пары
Оценки параметров отдельных величин
проводятся по тем же формулам, что и
выше, а оценка коэффициента корреляции
находится по формуле
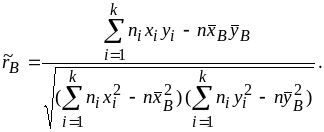(6.5.3)
В табл.8 нет одинаковых строк, но могут быть повторяющиеся значения Х и Y. В этом случае бывает удобно выборку представить в виде таблицы, которая по форме похожа на закон распределения дискретной случайной величины (табл.5).
Таблица 9
X |
|
|
Y |
|
|
|
|
... |
|
... |
|
|
|
... |
|
... |
|
... |
... |
... |
... |
... |
... |
|
|
... |
|
... |
|
... |
... |
... |
... |
... |
... |
|
|
... |
|
... |
|
В табл.9 среди
значений Х и среди значений Y
нет одинаковых,
- частота пары
Очевидно частота значения
определяется равенством
(6.5.4)
Частота значения
- формулой
(6.5.5)
Это позволяет использовать формулы (4.3.5) - (4.3.10) для нахождения оценок параметров отдельных величин. Оценка же коэффициента корреляции в этом случае определяется формулой
(6.5.6)
На основании данных выборки можно найти оценки коэффициентов линейного уравнения регрессии (уравнения средней квадратической регрессии). Уравнение регрессии Y на Х имеет вид
(6.5.7)
Уравнение регрессии Х на Y имеет вид
(6.5.8)
Пример 2. Найти оценки параметров и выборочные линейные уравнения регрессии по данным выборки, приведенной в таблице (в последних строке и столбце приведены частоты, найденные по формулам (6.5.4) и (6.5.5)).
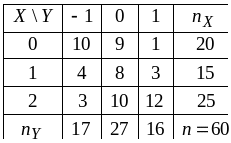
Вычисляем оценки математических ожиданий, дисперсий и средних квадратичных отклонений
Для вычисления оценки коэффициента корреляции удобно сначала вычислить суммы
Тогда оценка корреляции по формуле (6.5.6) равна
Уравнение регрессии Y на Х (6.5.7) имеет вид
и после вычислений
Уравнение регрессии Х на Y (6.5.8)
и окончательно имеем
