
1.3. Формула полной вероятности. Формула Бейеса
Пусть известны вероятности событий Н1, Н2, ... , Нn, составляющих полную группу попарно несовместимых событий и называемых гипотезами, и некоторое случайное событие А имеет различную вероятность, в зависимости от того, какая гипотеза оказалась верна, т.е. известны условные вероятности А в зависимости от того, какое Нi произошло: Р(A/Н1), P(A/Н2), ... , P(A/Нn).
Тогда безусловная (или полная) вероятность события А находится по формуле
![]() (1.3.1)
(1.3.1)
Пример 1. На складе имеются изделия трех цехов в отношении 2 : 3 : 5. Первый цех выпускает 90% изделий первого сорта, второй 80% и третий 70%. Какова вероятность, что наудачу взятое со склада изделие первого сорта?
Обозначим А - взятое изделие первого сорта. Об этом изделии можно высказать три гипотезы: Н1 - оно выпущено первым цехом, Н2 - вторым и Н3 - третьим. По условию 2 части всех изделий на складе составляют изделия первого цеха, 3 части - второго и 5 частей - третьего, всего таких частей 10 (2+3+5). Взятая наудачу деталь принадлежит одной из этих 10 частей, т.е. может быть 10 исходов, причем 2 исхода (2 части) благоприятны Н1, 3 исхода благоприятны Н2 и 5 исходов благоприятны Н3, поэтому
Р(Н1) = 0,2, Р(Н2) = 0,3 и Р(Н3) = 0,5.
Пусть на складе n
изделий первого цеха, тогда из них
первого сорта 90%, т.е. m
= 0,9
n.
Следовательно, Р(А/H1)
=
![]() Аналогично находим, Р(А/Н2)
= 0,8 и Р(А/Н3)
= 0,7. По формуле
полной вероятности
(1.3.1) получаем Р(А) = 0,2
0,9 + 0,3
0,8 + 0,5
0,7 = 0,77.
Аналогично находим, Р(А/Н2)
= 0,8 и Р(А/Н3)
= 0,7. По формуле
полной вероятности
(1.3.1) получаем Р(А) = 0,2
0,9 + 0,3
0,8 + 0,5
0,7 = 0,77.
Вернемся к началу этого параграфа и представим, что событие А произошло. Мы имеем некоторую новую информацию, повлияла ли она на вероятности гипотез? Т.е. решим задачу уточнения вероятностей гипотез при условии, что А произошло. Для этого нужно найти условные вероятности гипотез, которые находятся по формуле Бейеса
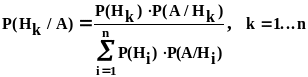 .
(1.3.2)
.
(1.3.2)
Пример 2. В условиях предыдущего примера ответить на вопрос: какова вероятность того, что взятое со склада первосортное изделие выпущено вторым цехом?
![]()
1.4. Независимые испытания. Формула Бернулли
Рассмотрим
последовательность независимых
испытаний, т.е. таких испытаний,
проводящихся последовательно, в каждом
из которых может произойти событие А с
постоянной вероятностью Р(А) = р. Испытания
являются независимыми, так как вероятность
события не зависит от номера испытания,
и результат каждого следующего испытания
не зависит от результатов предыдущих
испытаний. Иногда такие последовательности
испытаний называются испытаниями по
схеме Бернулли.
Обозначим вероятность противоположного
события Р(
)
= 1 - р = q
(p
и q
это стандартное обозначение вероятностей
взаимно противоположных событий,
p
+ q
= 1). Формула
Бернулли
позволяет найти вероятность того, что
в последовательности n
независимых
испытаний событие А произойдет ровно
k
раз. Такая вероятность обозначается
![]() или
или
![]()
![]() (1.4.1)
(1.4.1)
Пример 1. Найти вероятность того, что при 5 подбрасываниях игральной кости 6 очков выпадет 3 раза.
Очевидно, n
= 5, k
= 3, p
=
,
q
= 1 -
![]() и по формуле Бернулли (1.4.1) получим
и по формуле Бернулли (1.4.1) получим
![]()
Пример 2. Прибор при каждом включении может дать сбой с вероятностью 0,1. Какова вероятность того, что при 6 включениях произойдет не более двух сбоев?
В этом случае n = 6, p = 0,1, q = 0,9 и k = 0, или 1, или 2, поэтому
![]()
Пример 3. Какова вероятность того, что при 6-ти подбрасываниях игральной кости 6 очков выпадет не менее 2-х раз?
Убедитесь сами, что k = 2, или 3, или 4, или 5, или 6 и k = 0 или 1 - противоположные события.
Таким образом, искомая вероятность
![]()
