Минимальные требования.

1. Запишите материальные уравнения для среды с пространственной и временной дисперсией.

В среде с пространственной и временной дисперсией материальные уравнения имеют операторный вид

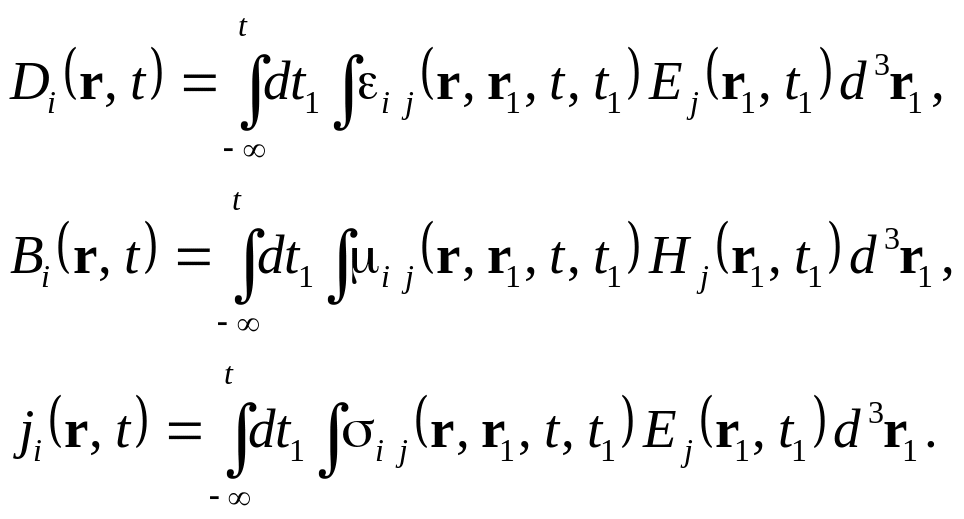
\\\2. Запишите материальные уравнения для нелинейной среды.

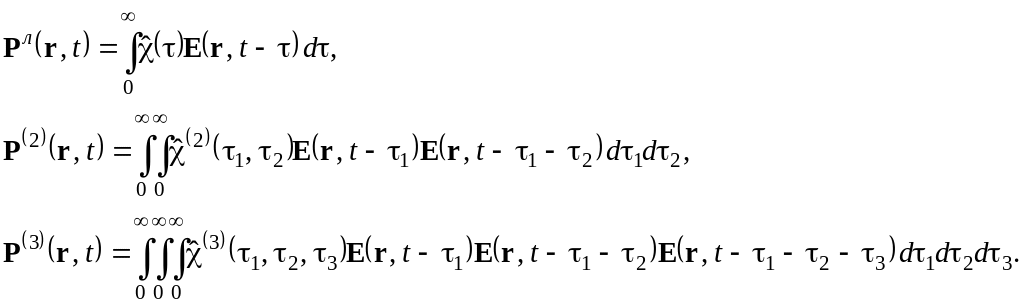
3. Что такое дисперсионное уравнение?

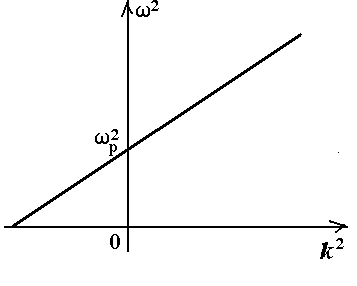
Рис. 2.2. Дисперсия в плазме

В разреженной плазме  ~ (10³ ... 10⁴) c^-1 и при  >>  проницаемость () чисто действительная, , то есть

– дисперсионное уравнение, его график приведен на рис. 2.2.

при  > _p коэффициент преломления n действительный и волна свободно распрос­т­ра­няется, при  < _p коэффициент преломления n мнимый, то есть волна отра­жа­ется от границы плазмы.

при  = _p в плазме возможно существование продольных (плазменных) волн.

\\\4. Что такое нормальные волны?

34 35

5. Запишите соотношение Крамерса – Кронига.

, ( 2.0)

, ( 2.0)

устанавливающие универсальную связь между действительной и мнимой частями комплексной проницаемости. Из соотношений Крамерса – Кронига, что диспергирующая среда является поглощающей средой.

6. Что такое оптически активные и гиромагнитные среды? Какими особенностями они

обладают?

Оптически активной может быть только среда без центра симметрии. Такая среда называется гиротропной и описывается несимметричным тензором диэлектрической проницаемости _{i j}(k, ) = _{j i}(–k, ) = ^*_{j i}(k, ).

. (2.0)

Двум значениям n² соответствуют две волны с правой и левой круговой поляризацией, из соотношения (1.38) следует, что . При этом, как следует из соотношения (2.32), фазовые скорости этих волн различны, что приводит к повороту плоскости поляризации линейно поляризованной волны при распространении в гиротропной среде (эффект Фарадея).

Распространение электромагнитных волн в гиромагнитных средах

В ферритах типа MeOFe₂O₃ (Me – двухвалентный металл) тензором является магнитная проницаемость _{i j}(). Анизотропия магнитной проницаемости в ферритах создается наложением постоянного или медленно (по сравнению с частотой электромагнитной волны) меняющегося магнитного поля Н. В ферритах магнитные моменты молекул, имеющие спиновую природу, из-за взаимодействия не компенсируются, и единица объема (домен) обладает магнитным моментом М, то есть является магнитным диполем. Прецессия магнитных диполей вокруг силовых линий постоянного магнитного поля и создает анизотропию магнитных свойств. При Н = 0 магнитная проницаемость феррита – скалярная величина.

Линейно поляризованная волна в продольно намагниченном феррите расщепляется на две волны, поляризованные по кругу. Скорости распространения этих волн различны, поэтому при прохождении некоторого расстояния l плоскость поляризации оказывается повернутой на угол, пропорциональный l (эффект Фарадея). Направление вращения плоскости поляризации определяется относительно вектора Н и не зависит от направления распространения волны (по z или по –z). Это свойство используется для создания СВЧ-вентильных систем (циркуляторов).