
- •1. Краткие теоретические сведения
- •1.1. Знакомство с функциями
- •1.2. Описание функции
- •1.3.1. Тело функции
- •1.3.2. Формальные параметры функции
- •1.3.3. Обращение к функции
- •1.3.4. Фактические параметры.
- •1.4. Формальные и фактические параметры функции
- •1.5. Описание и объявление функции. Прототип функции
- •1 Способ - Перед main().
- •2 Способ - После main ().
- •1.6. Передача параметров в функцию. Изменяемые значения параметров
- •1.6.1. Передача параметров
- •1.6.2. Передача параметров по значению
- •1.6.3. Передача параметров по ссылке
- •1.6.4. Передача параметров по указателю
- •1.7. Механизм обращения к функции и передача данных
- •1.8. Локальные и глобальные переменные. Время жизни и область действия (видимости) переменных
- •1.8.1. Представление об области видимости переменных
- •1.8.2. Объявление локальных переменных
- •1.8.3. О конфликте имен
- •1.8.4. Глобальные переменные
- •1.8.5. Если имена глобальных и локальных переменных конфликтуют
- •1.9. Принцип сокрытия данных внутри функции. Принцип локализации имен
- •1.10. Передача одномерных массивов как параметров функции
- •1.11. Передача многомерных массивов в функцию
- •1.12. Рекурсивные функции
- •1.13. Аргументы по умолчанию
- •1.14. Встраиваемые функции (inline)
- •1.15. Перегрузка функций
- •1.16. Указатель на функцию
- •1.17. Шаблоны функций
- •1.18. Использования библиотеки этапа выполнения
- •1.18.1. Использование функций библиотеки этапа выполнения
- •1.18.2. Изучение функций библиотеки этапа выполнения
- •1.18.3. Использование функций api
- •1.19. Изменение значений параметров функции
- •1.19.1. Почему функции обычно не могут изменить значения параметров
- •1.19.2. Изменение значения параметра
- •1.19.3. Использование ассемблерных листингов для лучшего понимания работы компилятора
- •1.20. Примеры решения задач с использованием механизма функций
- •2. Задание
- •2.4. Задания для выполнения на занятиях
- •2.4.1. Задание 1. Функции пользователя-использование формул
- •2.4.1.1. Условие задания
- •2.4.1.2. Пример для варианта 30
- •2.4.1.3. Программа
- •2.4.1.4. Тестирование
- •2.4.2. Задание 2. Функции пользователя при работе с массивами
- •2.4.2.1. Условие задания
- •2.4.2.2. Пример для варианта 30
- •2.4.2.3. Программа
- •2.4.2.4. Тестирование
- •2.4.3. Задание 3. Функции пользователя при работе с массивами
- •2.4.3.1. Условие задания
- •2.4.3.2. Пример для варианта 30
- •2.4.3.3. Программа
- •2.4.3.4. Тестирование
- •2.4.4. Задание 4. Вычисление выражений с использованием функций
- •2.4.4.1. Условие задания
- •2.4.4.2. Пример для варианта 30
- •2.4.4.3. Программа
- •2.4.4.4. Тестирование
- •2.4.5. Задание 5. Вычисление интеграла методом трапеций
- •2.4.5.1. Условие задания
- •2.4.5.2. Пример для варианта 30
- •2.4.5.3. Программа
- •2.4.5.4. Тестирование
- •2.4.5.5. Типичные ошибки при выполнении работы
- •Вопросы для самоконтроля
- •Литература
- •1. Краткие теоретические сведения 2
- •1.1. Знакомство с функциями 2
2. Задание
2.1. Изучить теоретические сведения.
2.1.1. Изучить операции сравнения.
2.1.2. Изучить логические операции.
2.1.3. Изучить приоритет операций.
2.1.4.Изучить понятие оператора перехода.
2.1.5. Изучить понятие составного оператора.
2.1.6. Изучить понятие пустого оператора.
2.1.7. Изучить понятие разветвляющегося вычислительного процесса.
2.1.8. Изучить средства языка С++ для реализации разветвляющегося вычислительного процесса.
2.1.9. формы условного оператора if/
2.1.10. Изучить оператор выбора switch.
2.2. Разобрать и выполнить примеры к данной лабораторной работе.
2.3. Написать и отладить семь программ на языке С++.
2.4. Задания для выполнения на занятиях
2.4.1. Задание 1. Функции пользователя-использование формул
2.4.1.1. Условие задания
Написать программу решения задачи с использованием механизма функций пользователя.
Таблица 13.1
№ |
Задание |
1 |
Определить периметры трёх треугольников, если заданы координаты их вершин. |
2 |
Вычислить сумму объёмов трёх шаров и сумму их поверхностей, если известны их радиусы. |
3 |
Даны четыре пары чисел: A, a, B, b, C, c, D, d, - которые являются соответственно наружными и внутренними радиусами колец. Найти общую площадь этих колец. |
4 |
Заданы координаты трёх точек. Подсчитать сумму их расстояний до начала координат. |
5 |
Заданы координаты четырёх точек. Подсчитать сумму их расстояний до точки с координатами (a,b). |
6 |
Падание
активности образца происходит по
следующему закону:
|
7 |
Концентрация вещества в реакторе изменяется по закону C = C0 (1− e−kt ). Определить среднюю концентрацию вещества в трёх реакторах, если для каждого реактора заданы начальная концентрация С0, время реакции t и константа скорости k. |
8 |
Рассчитать суммарную кинетическую энергию пяти частиц, движущихся со скоростями V1,V2,V3,V4,V5 близкими к скорости света C, и имеющих массу соответственно m1, m2, m3, m4, m5. Кинетическая энергия в этих условиях вычисляется по формуле:
|
9 |
Определить
среднюю высоту полёта аэростата,
если четыре измерения температуры
и давления дали результаты соответственно
T1, T2, T3, T4 и
P1, P2, P3, P4.
барометрическая формула:
|
10 |
Найти
электрическую ёмкость двухпроводной
линии, состоящей их четырёх участков
длиной l1, l2, l3, l4,
соответственно и с расстоянием между
проводами d1, d2, d3,
d4. Все провода имеют радиус a.
Формула емкости линии:
|
11 |
Вычислить
среднюю скорость, осаждения смеси
частиц диаметром от d1 до d2
плотностью от r1 до r2, если
скорость осаждения может быть
вычислена по формуле
|
12 |
Вычислить сумму объёмов и сумму поверхностей четырёх цилиндров, если для каждого из них известны высота и радиус основания. |
13 |
Главный
центральный момент инерции тора
относительно оси, перпендикулярной
к его плоскости, вычисляется по
формуле
|
14 |
Ёмкость
сферического конденсатора вычисляется
по формуле
|
15 |
Напряжённость
магнитного поля в центре прямоугольного
витка с током I рассчитывается по
формуле
|
16 |
Определить сумму объёмов и сумму поверхностей трёх прямоугольных параллелепипедов, если известны их измерения. |
17 |
Главный
центральный момент инерции сплошного
шара определяется по формуле |
18 |
Ёмкость
цилиндрического конденсатора с
длиной l и радиусами внутреннего
и внешнего цилиндров, равными r1
и r2, вычисляется по формуле
|
19 |
Вычислить сумму объёмов и сумму полных поверхностей трёх круглых конусов, если для каждого конуса известны высота и радиус основания. |
20 |
Главный
центральный момент инерции полого
шара массой m с радиусами внешней и
внутренней поверхностей, равными R1
и R2, вычисляется по формуле
|
21 |
Ёмкость
сферического конденсатора вычисляется
по формуле
|
22 |
Концентрация
вещества в реакторе растёт по закону
|
23 |
Найти сумму площадей трёх треугольников, если известны длины их сторон (для вычисления площади использовать формулу Герона). |
24 |
Главный
центральный момент инерции тора
относительно оси, лежащей в его
плоскости, вычисляется по формуле
|
25 |
Ёмкость
цилиндрического конденсатора
вычисляется по формуле
|
26 |
Напряжённость
поля, создаваемая точечным зарядом
вычисляется по формуле
|
27 |
Работа по перемещению заряда в однородном поле вычисляется по формуле A = q ⋅ E ⋅ d , где q – заряд, E – напряжённость поля, d – расстояние между двумя точками электрического поля. Вычислить общую работу для трёх зарядов, если для каждого из них известны величина заряда q, E и d. |
28 |
Ёмкость
плоского конденсатора рассчитывается
по формуле |
29 |
Сопротивление
рассчитывается по формуле
|
30 |
Рассчитать среднюю работу по перемещению заряда в однородном поле для трёх зарядов, если для каждого из них известны величина заряда q, напряжённость E, расстояние между двумя точками d. Работа вычисляется по формуле A = q ⋅ E ⋅ d . |

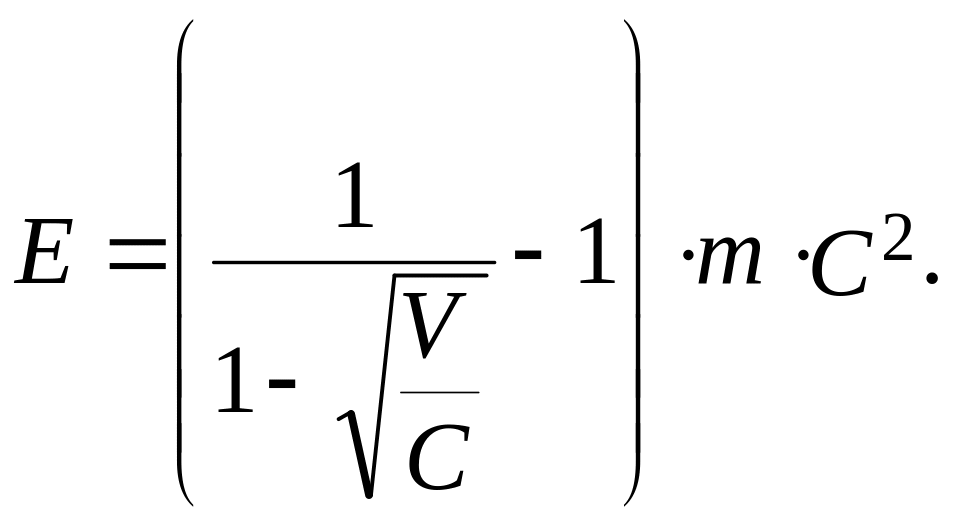
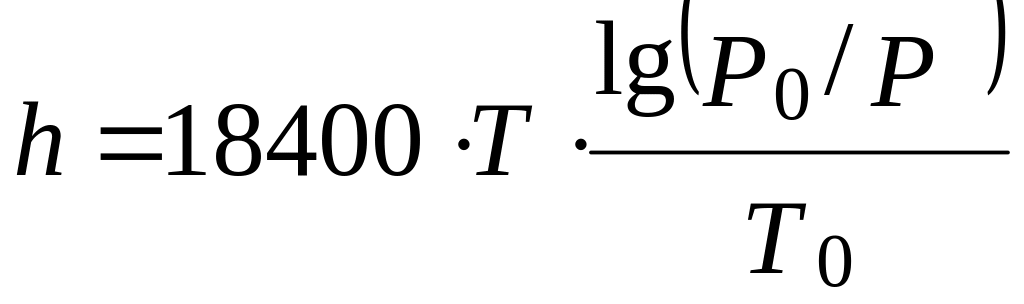 ,
где P0=760 мм рт. ст., T0=273,15
К.
,
где P0=760 мм рт. ст., T0=273,15
К.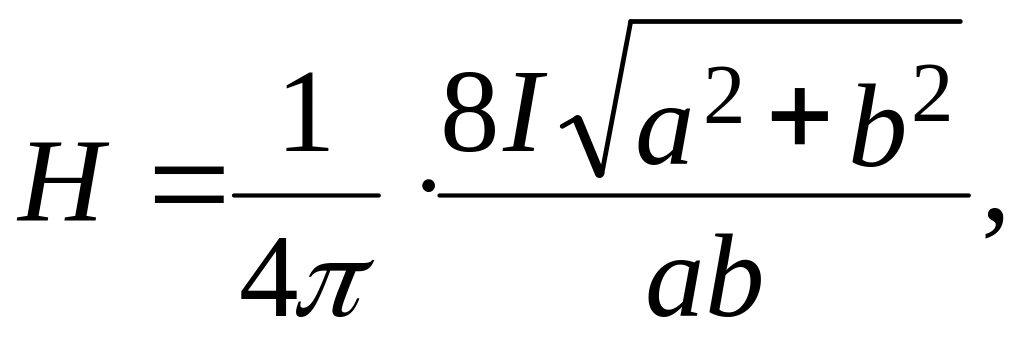 где
a и b – длины сторон прямоугольника.
Найти напряжённость магнитного поля
в общем центре трёх прямоугольных
витков, лежащих в одной плоскости.
Если для каждого из них известны
размеры и значения силы тока I (ток
во всех витках проходит в одном
направлении).
где
a и b – длины сторон прямоугольника.
Найти напряжённость магнитного поля
в общем центре трёх прямоугольных
витков, лежащих в одной плоскости.
Если для каждого из них известны
размеры и значения силы тока I (ток
во всех витках проходит в одном
направлении).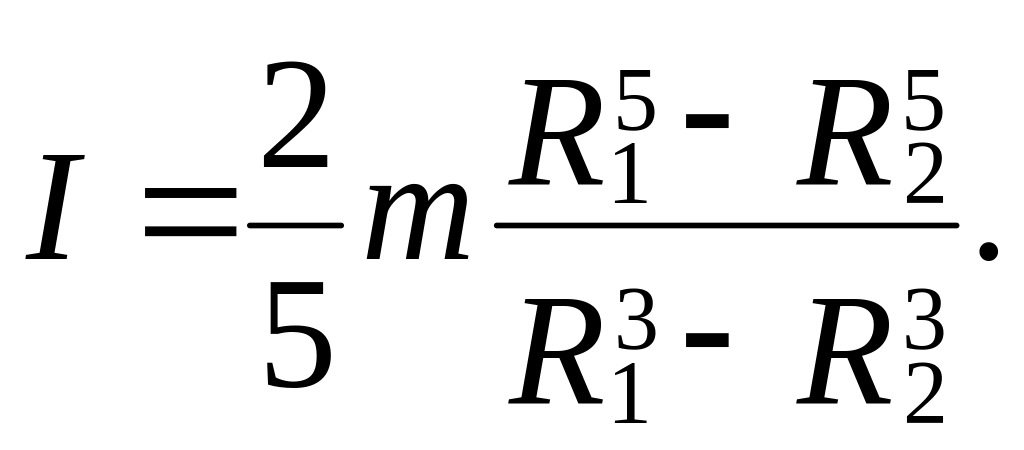 Найти
среднее значение I для трёх полых
шаров с известными значениями m, R1,
R2.
Найти
среднее значение I для трёх полых
шаров с известными значениями m, R1,
R2.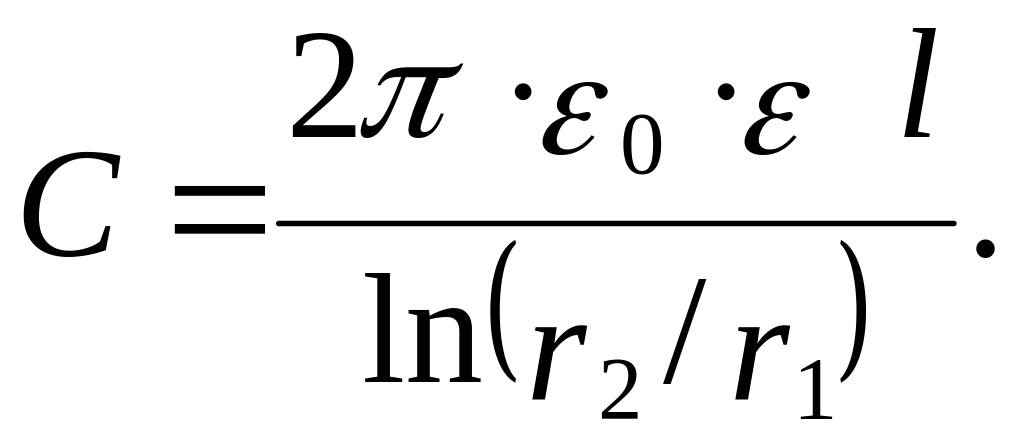 Здесь
l – длина конденсатора, r1,
r2 – радиусы внутреннего и
внешнего цилиндров, соответственно.
Найти общую ёмкость трёх последовательно
соединённых конденсаторов, если для
каждого из них известны значения l,
r1, r2, а 0*=8,85*10-12
Ф/м.
Здесь
l – длина конденсатора, r1,
r2 – радиусы внутреннего и
внешнего цилиндров, соответственно.
Найти общую ёмкость трёх последовательно
соединённых конденсаторов, если для
каждого из них известны значения l,
r1, r2, а 0*=8,85*10-12
Ф/м.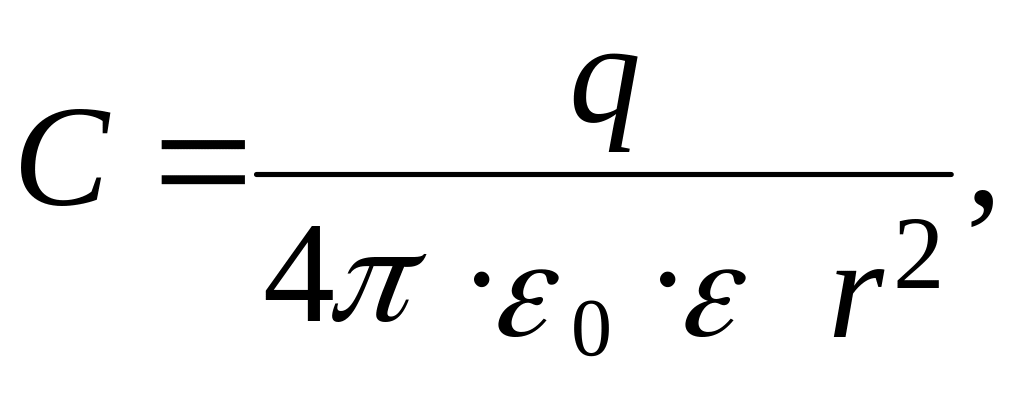 где
q – заряд создающий поле, 0*=8,85*10-12
Ф/м, r – расстояние от q до точки. Найти
общую напряжённость поля для трёх
зарядов, если для каждого из них
известны величина заряда q и расстояние
r.
где
q – заряд создающий поле, 0*=8,85*10-12
Ф/м, r – расстояние от q до точки. Найти
общую напряжённость поля для трёх
зарядов, если для каждого из них
известны величина заряда q и расстояние
r.