8.10. Метод простого случайного поиска
Алгоритм
этого метода можно отнести к классу
разветвляющихся. Запишем этот алгоритм
применительно к компоненту
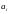вектора
.
n – номер итерации.
(8.19)
На
очередном приближении
вычисления компоненты
вектора
генерируется с помощью случайного
механизма компонента вектора
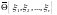(где
- заданное число случайных проб), тогда
при выполнении условия целевой функции
с данным случайным приращением компоненты
в сторону уменьшения
(8.20)
cчитается,
что данная случайная проба успешна и
очередное приближение
записывается как
.
Если же для очередной случайной пробы
условие (8.20) не выполняется, компонента
сохраняет предыдущее значение и случайная
проба считается неудачной.
Все неудачные пробы запоминаются на текущем значении рабочего шага .
- масштабный коэффициент
выбирается
для каждого компонента вектора, чтобы
в случае нарушения ограничения
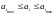(8.21) удерживать значение
на верхней или нижней границе.
Если
число неудачных случайных проб
достигнет заданной величины
,
считают очередной цикл оптимизации
случайным поиском неудачным и повторяют
алгоритм (8.19) с новым значением рабочего
шага:
Величина
определяет точность оптимизации, при
этом условием окончания цикла по
считают
(8.22).
Метод
простого случайного поиска оптимальных
параметров сложной системы рекомендуется
применять для нахождения вектора
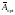большой размерности (
).
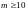8.11 Алгоритм случайного поиска по наилучшей пробе
Для
повышения эффективности применения
идеи случайного поиска (смотри предыдущий
алгоритм) используют модификации метода
простого поиска, заключающиеся в
генерации вектора
как случай нового приращения компонент
вектора
,
который отвечает условиям
:
,
Где
включает
случайных пробных шагов,
- диагональная матрица масштабных
коэффициентов.
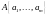
называется
матрицей чувствительности критерия
эффективности
к изменению оптимизируемых параметров
вектора
,
при этом вводится понятие наилучшей
пробы, которую для приращения вектора
обозначим:
,
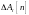Эффективность
алгоритма зависит от начального
приближения этой наилучшей пробы
.
Условия правильного движения к экстремуму
целевой функции формируется в виде 2-ух
компонент:
(8.23)
На всем множестве случайных проб наилучшей пробой считается та, которая обеспечивает сходимость критерия качества к min значению. Второе условие, которое должно выполняться совместно с условием (8.23) запишем:
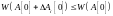(8.24)
Если
на первом шаге
процедуры оптимизации вычислено
значений критерия эффективности
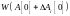и выполняются совместно условия (8.23) и
(8.24), то с учетом определения наилучшей
пробы алгоритм оптимизации может быть
записан:
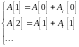(8.25)
и
подобная процедура (8.25) позволяет
вычислить на шаге
наилучшую пробу
.
Условием движения к оптимуму по наилучшей пробе проверяются с помощью следующих выражений:
(8.26)
Оптимизация
по наилучшей пробе методом случайного
поиска представляет собой итерационную
процедуру, при этом, если на каком-либо
значении рабочего шага
нарушаются условия (8.26), этот шаг
и рабочий шаг оптимизации
изменяется по такому правилу:
Изменение происходит в сторону уменьшения шага и движения в выбранном направлении продолжается в сторону полученной пробы, причем для каждого компонента вектора сохраняется итерационная процедура
,
Если нарушаются граничные условия, то
(8.27)
Условием
завершения параметрической оптимизации
на шаге
будет выполнение условия
.
Алгоритм поиска по наилучшей пробе рекомендуется при параметрической оптимизации больших систем.