8.8 Метод и алгоритм параметрической оптимизации. Движение по антиградиентному направлению

Использование данного метода предпочтительнее, если известны ограничения на оптимизируемые параметры типа неравенств или равенств и если в процессе оптимизации имеет место нарушение этих ограничений.

Алгоритм требует задания начального значения вектора оптимизируемых параметров для каждого его компонента. Источником этих данных является результат параметрического анализа математической модели объекта оптимизации.

Если критерий оптимизации не имеет законченного аналитического описания, то алгоритм требует выполнить оценку этого критерия, что также возможно с использованием вероятностной модели объекта оптимизации.

При вычислении градиента целевой функции рекомендуют использовать численную оценку градиента, полученную методом конечных разностей.

8.8.1 Шаги алгоритма при движение по антиградиентному направлению

1. Для i-го компонента вектора a_i n-го шага оптимизации можно записать, что

(8.13) - рабочий шаг

- масштабные коэффициенты, зависящие от ограничений, накладываемых на оптимизируемый параметр

Границы и заданы в явном виде.

2. Расчет масштабных коэффициентов.

Если в процессе реализации выражения (8.13 ) какой-либо из компонент выходит на заданную границу или пересекает ее или 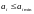, то процесс оптимизации продолжается, а данный компонент вектора получает значение или .

(8.14)

3. Если выражение для критерия оптимизации не позволяет вычислить градиент в явном виде, то используется его конечно-разностная оценка

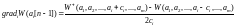(8.15)

Оценка градиента по выражению (8.15) может выполняться не на каждом рабочем шаге n, что позволяет сократить время оптимизации.

4. При нарушении ограничений типа (8.14) по всем компонентам вектора A для обеспечения сходимости процедуры (8.13) шаг уменьшают в k раз и продолжают итерационный процесс.

Движение по анти градиентному направлению происходит до тех пор, пока очередное значение критерия оптимизации убывает по отношению к предыдущему

_(8.16)

Если же условие (8.16) нарушается в каком-либо из циклов, то выполняют оперативную корректировку рабочего шага . и проверяется условие = _(8.17)

При неоднократном применении условия ()8.17 для окончания процесса оптимизации проверяют следующее условие (8.18)

Использование для окончания процесса оптимизации условий (8.17) или (8.18) позволяет в интерактивном режиме управлять процессом (8.13), при этом ограничения других алгоритмов связанные с величиной параметра m, в данном случае снимается.

8.9 Параметрическая оптимизация мп сау омт методами случайного поиска

На рис.8.4 приведены методы параметрической оптимизации МП САУ ОМТ.

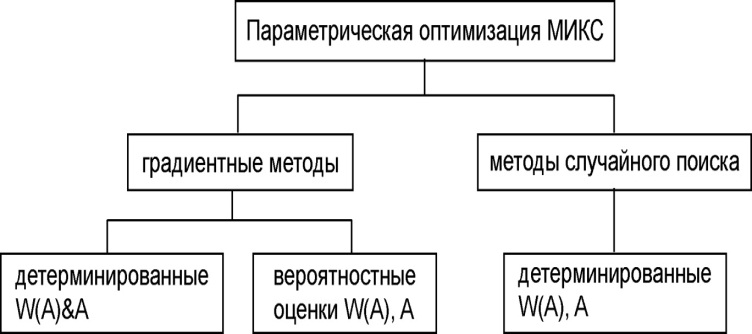
Рис.8.4 Методы параметрической оптимизации МП САУ ОМТ.

_{Если для детерминированных методов оптимизации условием выбора оптимального} является выполнение условия:

или для ряда методов , а точность решения определялась заданием минимального значения рабочего шага , то для метода случайного поиска путь движения к глобальному экстремуму функции уже не может быть определен с использованием градиента целевой функции .

Для методов случайного поиска экстремум функции определяют, генерируя механизм создания случайного шага для поиска экстремума функции .

Введем следующие обозначения для :

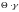- рабочий шаг оптимизации,

- нормированный случайный вектор, распределенный заданным способом в m-мерной сфере).