8.5 Метод оптимизации наискорейшего спуска с постоянным рабочим шагом
-
начальное приближение вектора
оптимизируемых параметров;
-
критерий оптимизации, явно заданный в
виде аналитического выражения;
-
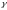рабочий шаг оптимизации;
-
номер итерации в методе наискорейшего
спуска.
Алгоритм
определения
-го
приближения вектора
имеет вид:
(8.2)
Для начала работы алгоритма нужно вычислить:
Ограничения
на вектор оптимизируемых параметров
можно задать как принадлежность его
некоторой области
,
за пределами этой области решение
считаем невозможным, а на границах
области допустимым.
Запишем
два первых приближения вектора
,
используя выражение (8.2):
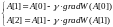(8.3)
Для оценки сходимости последовательности (8.3) используют понятие предела и если он существует, то вводится численная оценка сходимости последовательности (8.3) в виде:
(8.4)
Предел:
Для метода наискорейшего спуска значение рабочего шага определяет приращение вектора оптимизируемых параметров, которое записывается так:
(8.5)
Выбор
же текущего значения рабочего шага
зависит как от
(очередного приближения оптимизируемого
вектора), так и от градиента критерия
качества
,
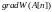для которого мы введем обозначение
(набла).
(8.6)
8.6. Разновидности алгоритмов параметрической оптимизации, использующие метод наискорейшего спуска
Выбор
конкретного алгоритма оптимизации
зависит от способа задания рабочего
шага
.
В общем случае рабочий шаг на
-ом цикле оптимизации
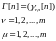(8.7)
Тогда для выражения (8.7) алгоритм оптимизации можно записать следующим образом:
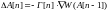(8.8)
Алгоритмы
типа (8.8) называют релаксационными
методами оптимизации, конкретные
выражения для которых зависят от свойств
матрицы (8.7). Пусть компоненты матрицы
будут постоянными и не зависят от номера
итерации
.
.
Тогда
одним из способов получения этих
компонент будет их вычисление по правилу:
(8.9)
Алгоритм
оптимизации типа
(8.10)
называют
алгоритмом Ньютона. Обычно используется
выражение (8.10) или его разновидность
(8.11)
Если
использование алгоритмов (8.10) или (8.11)
не обеспечивает требуемой сходимости,
то рекомендуется использование
модифицированного метода Ньютона, в
котором компоненты матрицы
выбирают переменными на каждой итерации
.
(8.12)
Для
вычисления матрицы
используется формула
.
-
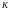единичная матрица
-скалярная
величина, зависящая от текущего
Релаксационные
алгоритмы параметрической оптимизации
обеспечивают получение локального
оптимума, зависящего от выражени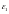й
и
.
Задача достижения глобального оптимума
решается вводом ограничений на вектор
непосредственно в критерий качества
.
8.7 Оценка градиента критерия оптимизации при отсутствии его аналитического описания
Для
получения оценки
,
где
имеет конечную размерность
,
используют понятие конечных разностей
и для простейшего случая первых разностей
записывают градиент таким образом:
Величина
зависит от конкретного выражения для
вектора
и выбирается после оценки чувствительности
критерия
к изменению компонент вектора
.