4.6 Синтез преобразователя внутренних кодов на примере дополнительного кода.

Различают алгоритмы арифметических и логических типов формирования дополнительных кодов. Алгоритмы первого типа требуют для реализации последовательностных цифровых схем, т.е. схем с элементами памяти. При этом для получения дополнительного n- разрядного двоичного кода до 2ⁿ необходимо выполнить инверсию этого кода и суммировать с единицей младшего разряда.

Подобные алгоритмы реализуют на параллельных регистрах в универсальных обработчиках информации. Альтернативой подобных алгоритмов для КЛС может служить алгоритм, синтезируемый с использованием следующей таблицы истинности (табл.4.9):

Таблица 4.9

10 эквив.	Двоичный код					Дополнительный код					10 эквив.
	В4	В3	В2	В1	D4		D3	D2	D1
0	0	0	0	0	0		0	0	0	0
1	0	0	0	1	1		1	1	1	15
2	0	0	1	0	1		1	1	0	14
3	0	0	1	1	1		1	0	1	13
4	0	1	0	0	1		1	0	0	12
5	0	1	0	1	1		0	1	1	11
6	0	1	1	0	1		0	1	0	10
7	0	1	1	1	1		0	0	1	9
8	1	0	0	0	1		0	0	0	8
9	1	0	0	1	0		1	1	1	7
10	1	0	1	0	0		1	1	0	6
11	1	0	1	1	0		1	0	1	5
12	1	1	0	0	0		1	0	0	4
13	1	1	0	1	0		0	1	1	3
14	1	1	1	0	0		0	1	0	2
15	1	1	1	1	0		0	0	1	1

Синтез преобразователя двоичных кодов в дополнительный на базе КЛС выполним начиная с младшего разряда, для этого составим матицу Карно для функции D₁=F(B₄, B₃, B₂,B₁).

В4, В3
00 01 11 10
	В2,B1	00	0	0	0	0
		01	1	1	1	1
		11	1	1	1	1
		10	0	0	0	0

D₁=B₁

В4, В3
00 01 11 10
	В2,B1	00	0	0	0	0
		01	1	1	1	1
		11	0	0	0	0
		10	1	1	1	1

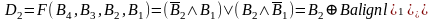
В4, В3
00 01 11 10 00
	В2,B1	00	0	1	1	0		0
		01	1	0	0	1		1
		11	1	0	0	1		1
		10	1	0	0	1		1
		00	0	1	1	0

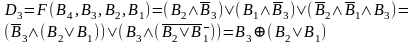
В4, В3
00 01 11 10
	B2,B1	00	0	1	0	1
		01	1	1	0	0
		11	1	1	0	0
		10	1	1	0	0

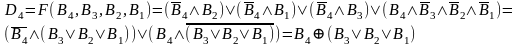
Логический алгоритм синтеза устройства для формирования n–разрядного дополнительного кода может быть представлен для любого разряда выражением вида :

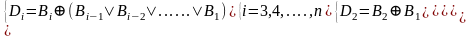
Дополнив его выражениями для D₁, D₂, получим замкнутый алгоритм для получения дополнительного кода.