6 Этап синтеза: численная оценка компонент критерия синтезируемой схемы.

Минимум аппаратных затрат может быть оценен суммарным числом выходов и входов используемых в схеме логических элементов:

MIN_A =  ВХ _i +  ВЫХ j =6+3=9

Оценка быстродействия связана с количеством каскадов (ступеней) используемых для построения схемы:

MAX_Б = 2

4.4 Синтез специальных комбинационных логических схем ( клс), используемых в мп сау.

При использовании критериев min аппаратных затрат и max быстродействия в задаче синтеза специальных логических схем , необходимо обосновать выбор элементной базы, обеспечивающей сопряжение синтезируемых схем с аппаратурой, для которой они предназначены. Часто затраты на устройство сопряжения превышают затраты на разработку собственно КЛС. Это и является причиной, мотивирующей создание специальных КЛС. Как правило, назначение этих схем специализировано, но решаемые ими задачи могут быть многократно востребуемы в МП САУ.

4.4.1 Синтез схемы для выполнения функции контроля нечётности двоичных кодов.

В качестве элементной базы, в зависимости от принципов построения МП САУ, на которые ориентируется синтезируемая схема, могут использоваться:

1. Логические элементы суммирования по модулю 2 ( М2) см. рис.4.7:

Рис.4.7 Логическая схема сложения по модулю 2.

Эти элементы имеют только два входа и предполагают использование параллельно-последовательных или параллельных схем их соединения при реализации функции нечетности.

В случае четного числа разрядов контролируемого кода предпочтительнее использование параллельной схемы (рис.4.8), обеспечивающей min критерию аппаратных затрат (4.3).

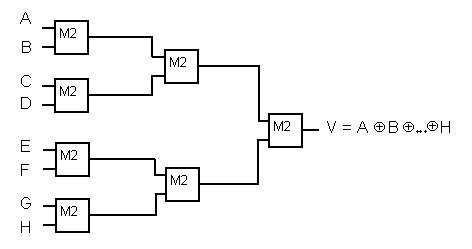
Рис.4.8 Параллельная логическая схема контроля нечетности двоичного кода.

К_А = ВХ _i +  ВЫХ j =14+7=21 (4.3)

К_В1 =3*_М2

При произвольном числе разрядов контролируемого кода возможно использование параллельно-последовательной

схемы (рис.4.9) на элементах M2.

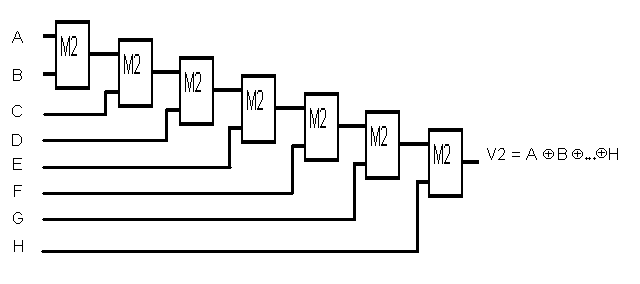
Рис.4.9 Параллельно-последовательная логическая схема контроля нечетности двоичного кода.

К_{А 2} =14+7=21

К_{А 1} = К_{А 2}

К_{Б 2} =7*_М2

При использовании произвольной элементной базы необходимо выполнить этапы синтеза, перечисленные ранее. Рассмотрим эту последовательность этапов для 3-х разрядного кода:

СДНФ:

F(A,B,C) = (A &B & C)  (A & B & C)  (A &B &C)  (A & B & C)

Таблица 4.4

Десятичный эквивалент	А В С	F(А,В,С)
0 1 2 3 4 5 6 7	0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1	0 1 1 0 1 0 0 1

Преобразуем F к минимальной форме, используя графоаналитический метод .Графоаналитический метод бесполезен для случая табл.4.5. С его помощью нельзя получить минимальную форму логической функции.

Преобразуем исходную функцию, используя дистрибутивные законы (4.4) и постоим схему (рис.4.10).

F(A,B,C) = (((A & B)(A &B))&C)  (((A &B)(A & B))& C)= ((A  B)&C)  ((A  B)& C )= A  B  C (4.4)

Таблица 4.5

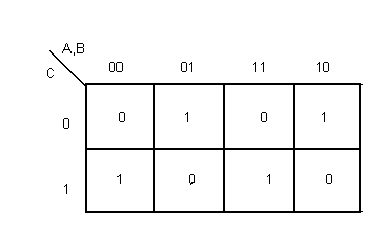
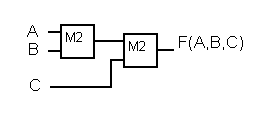
Рис.4.10 Синтезированная логическая схема

В зависимости от элементов, на которых построена основная система, синтезируемая схема может использовать:

1. Элементы И-ИЛИ :

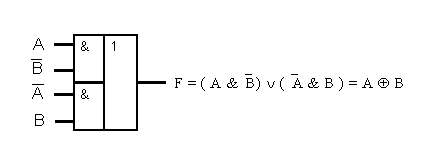
2. Активные элементы И-ИЛИ-НЕ :

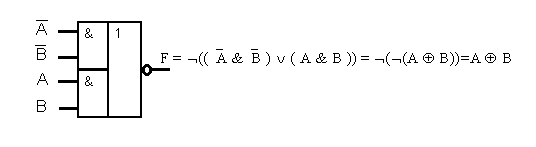
3. Элементы И-НЕ (штрих Шеффера):

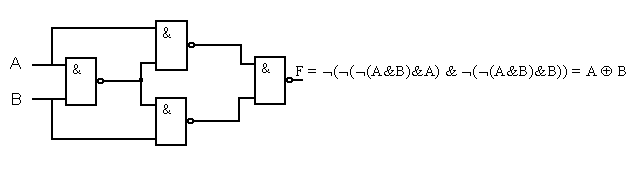
4. Элементы ИЛИ-НЕ (стрелка Пирса):

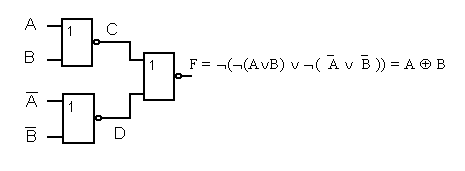
Используя перечисленные элементы ,решим задачу контроля кодированной информации в МП САУ.