3.7.7.6 Выход из рабочего колеса при конечном числе лопаток

Рассмотрим более подробно распределение давлений и скоростей в рабочем колесе с прямыми лопатками (Error: Reference source not found).

– Давления и скорости в межлопаточном канале РК

При бесконечно большом числе лопаток масса газа в межлопаточных каналах бесконечно мала, поэтому действие сил инерции, в том числе и кориолисовых, ничтожно, поток воздуха движется в относительном движется по направлению лопаток. В случае прямых лопаток имеет чисто радиальное направление, а сама скорость равна некоторому значению , так как .

При конечном числе лопаток играет роль масса воздуха, что приводит к появлению кориолисовых сил инерции. В результате возникает циркуляционное течение в направлении, обратном вращению, как отмечалось в разделе (Рисунок 9).

Как следствие, вдоль набегающей стороны а–а – скорость снижается на величину , а вдоль стороны b–b – увеличивается на величину . Как следствие этого [Error: Reference source not found], появляется в треугольнике скоростей дополнительная окружная составляющая скорости относительного движения (Рисунок 10). Индекс «S» происходит от английского «slip» или немецкого «der Schlupf», что на русском означает «скользнуть».

Как видно на треугольнике скоростей (Рисунок 10), это «проскальзывание», которое выражено составляющей , направленно против вращения, увеличивает угол и уменьшает угол , вследствие чего уменьшает закрутку потока на выходе :

,

что в свою очередь ведёт к уменьшению теоретического напора (14):

	.
– Треугольник скоростей на выходе из РК		– Зависимость коэффициента напора от угла и относительной скорости [Error: Reference source not found]

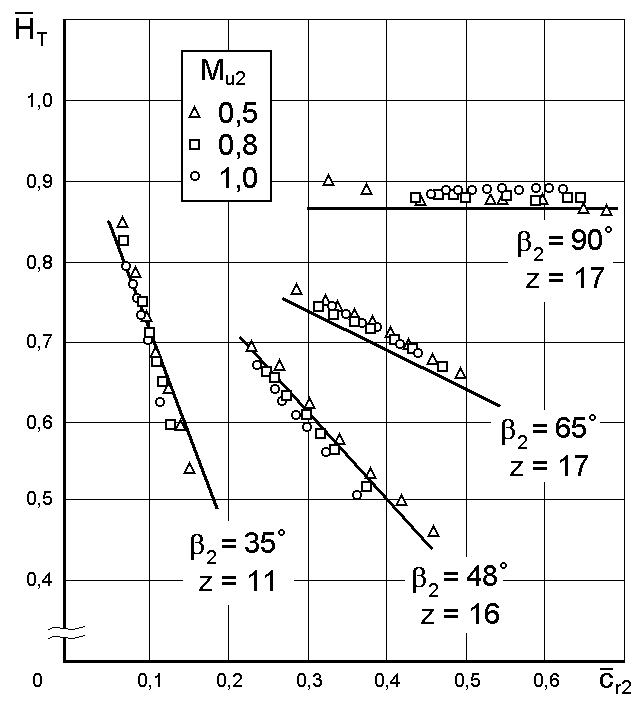
На графике (Рисунок 11) приведены эмпирические данные теоретического напора испытанных ЦБК. Видно, что теоретический напор ЦБК с конечным числом лопаток ниже чем теоретический напор ЦБК с бесконечным числом лопаток (Рисунок 8), но характер прямых одинаков (при проходит через для ; стремятся к для ).

Снижение фактического теоретического напора по сравнению с  (то есть при бесконечно большом числе лопаток) учитывается коэффициентом отставания потока, который иногда ещё называют коэффициентом циркуляции или коэффициентом передаваемой энергии (в английской литературе «slip factor»):

,

теоретическому и экспериментальному определению которого посвящено большое количество работ.

С помощью эмпирических формул для коэффициентом отставания потока , на основании кинематического угла и других, заранее определенных параметров, вычисляется лопаточный угол . На графике (Рисунок 12) приведена зависимость лопаточного угла от числа лопаток рабочего колеса для пяти разных эмпирических формул коэффициента отставания потока.

– Зависимость угла от числа лопаток и принятой формулы расчёта коэффициента отставания потока (график построен для РК: ; ; ; )

Самая простая эмпирическая формула для коэффициента отставания потока получена Виснером (Wiesner). Она основана на научных работах Стодолы (Stodola). Её предпочтительно рекомендуют применять при [Error: Reference source not found]:

.

Следующая эмпирическая формула также получена Виснером на основании работ Стодолы, Бусаманна (Busemann) и Станице (Stanitz) [Error: Reference source not found]:

.

Учебник Ржавина ([Error: Reference source not found], стр.141) рекомендует следующую формулу:

.

Далее из литературы ([Error: Reference source not found], стр. 78) известны следующие две формулы:

.
.

Какая из перечисленных формул более точно отражает истину, вопрос. Глядя на график (Рисунок 12) видно, что определение по разным формулам даёт отклонение для угла примерно , поэтому примерно с такой же погрешностью можно ожидать точность расчёта коэффициента отставания потока .

Проскальзывание определяется методом последующих итераций по формуле:

.

Для первой итерации в коэффициент отставания потока вместо лопаточного угла  подставляется заранее подсчитанный кинематический угол , вычисляется первое приближение проскальзывания и первое приближение лопаточного угла , которое в свою очередь вставляется в коэффициент отставания потока второй итерации . Для того, чтобы значение лопаточного угла сошлось до десятичных, требуется не более пяти итераций.

Теоретический напор (30) можно выразить и преобразовать. Получим связи относительных скоростей с коэффициентом теоретического напора:

	.
	.
	.