Раздел III. Ряды динамики

3.1. Имеются данные об изменении показателей предприятия за 7 лет.

Таблица 3.1

№ п/п	Годы	Коэффициент износа ОПФ, %
1	1993	1,27
2	1994	1,36
3	1995	1,50
4	1996	1,37
5	1997	1,19
6	1998	1,11
7	1999	1,17

3.2. Для каждого года данного периода рассчитать показатели изменения коэффициента износа ОПФ.

а) абсолютные приросты

1,50 – 1,36=0,14

=1,37 – 1,27= 0,10 -0,13

-0,18

-0,08

0,06

б) коэффициент роста и темп роста

К^баз_р=у_i/у₁ К^цеп_р=у_i/у_i-1

К^баз₁₉₉₄=1,36/1,27=1,07 К^цеп₁₉₉₄=1,36/1,27=1,07

К^баз₁₉₉₅=1,50/1,27= 0,88 К^цеп₁₉₉₅=1,50/1,36=1,10

К^баз₁₉₉₆=1,37/1,27=0,81 К^цеп₁₉₉₆=1,37/1,50=0,91

К^баз₁₉₉₇=1,19/1,27=0,70 К^цеп₁₉₉₇=1,19/1,37=0,86

К^баз₁₉₉₈=1,11/1,27=0,87 К^цеп₁₉₉₈=1,11/1,19=0,93

К^баз₁₉₉₉=1,17/1,27=0,92 К^цеп₁₉₉₉=1,17/1,11=1,05

T^баз_р=у_i/у₁*100% T^цеп_р=у_i/у_i-1*100%

T^баз₁₉₉₄=107% T^цеп₁₉₉₄=107%

T^баз₁₉₉₅=88% T^цеп₁₉₉₅=110%

T^баз₁₉₉₆=81% T^цеп₁₉₉₆=91%

T^баз₁₉₉₇=70% T^цеп₁₉₉₇=86%

T^баз₁₉₉₈=87% T^цеп₁₉₉₈=93%

T^баз₁₉₉₉=92% T^цеп₁₉₉₉=105%

в) темп прироста

T^баз_пр= T^баз_р-100 T^цеп_пр=T^цеп_р-100

T^баз_{пр 1994}=7% T^цеп_{пр 1994}=7%

T^баз_{пр 1995}=-12% T^цеп_{пр 1995}=10%

T^баз_{пр 1996}=-19% T^цеп_{пр 1996}=-9%

T^баз_{пр 1997}=-30% T^цеп_{пр 1997}=-14%

T^баз_{пр 1998}=-13% T^цеп_{пр 1998}=-7%

T^баз_{пр 1999}=-8% T^цеп_{пр 1999}=5%

г) абсолютное значение 1% прироста

∆^цеп_1%=∆^цеп/ T^цеп_пр

∆^цеп₁₉₉₄=0,09/7=0,01%

∆^цеп₁₉₉₅=0,14/10=0,014%

∆^цеп₁₉₉₆=(-0,13)/(-9)=0,014%

∆^цеп₁₉₉₇=(-0,18)/(-14)=0,013%

∆^цеп₁₉₉₈=(-0,08)/(-7)=0,011%

∆^цеп₁₉₉₉=0,06/5=0,012%

3.3. Рассчитать средние показатели ряда динамики.

а) средний уровень ряда

=(1,27+1,36+1,50+1,37+1,19+1,11+1,17)/7=7,97

б) средний абсолютный прирост

=(1,17-1,27)/(7-1)=-0,1/6=-0,016

в) средний темп роста

;

г) средний темп прироста

3.4.Произвести сглаживание ряда динамики с помощью метода скользящей средней.

Применим трехчленную скользящую

Таблица 3.2

Годы	Уровни	Подвижные нецентрированные суммы	Подвижные средние нецентрированные	Подвижные двухчленные суммы	Центрированные скользящие средние
1993	1,27
1994	1,36	4,13	4,13/3=1,37
1995	1,50	4,23	4,23/3=1,41
1996	1,37	4,06	4,06/3=1,35
1997	1,19	3,67	3,67/3=1,22
1998	1,11	3,47	3,47/3=1,15
1999	1,17

3.5. Произвести аналитическое выравнивание ряда динамики

Уравнение прямой линии: У_t=A_o+A₁*t

С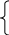 пособ "наименьших квадратов" дает следующую систему нормальных уравнений:

nA_o+ A₁∑ t= ∑У;

A_o ∑ t+A₁ ∑t²= ∑У*t

Упростим уравнения

Таблица 3.3.

Годы	1993	1994	1995	1996	1997	1998	1999
Уровни ряда динамики	У1 1,27	У2 1,36	У3 1,50	У4 1,37	У5 1,19	У6 1,11	У7 1,17
Условное начало отсчета	t=-3	t=-2	t=-1	t=0	t=1	t=2	t=3

n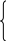 A_o = ∑ У ; A_o = ∑ У/n

A₁ ∑ t²= ∑У*t A₁= ∑ У*t/ ∑t²

Вспомогательная таблица для расчетов параметров уравнения

Таблица 3.4.

Годы	Уровни,% (У)	t	t*У	t2	Уt=Ao+A1*t
1993	1,27	-3	-3,81	9	1,4
1994	1,36	-2	-2,72	4	1,36
1995	1,50	-1	-1,50	1	1,32
1996	1,37	0	0	0	1,28
1997	1,19	1	1,19	1	1,24
1998	1,11	2	2,22	4	1,20
1999	1,17	3	3,51	9	1,16
	∑8,97	∑0	∑-1,11	∑28

A_o =176,9/7=25,27

A₁=-7,8/28=-0,28

У_t=25,27-0,28*t

3.6. Произвести экстраполяцию ряда динамики на 2 года вперед

У₂₀₀₀=1,28-0,04*4=1,12, t=4

У₂₀₀₁=1,28-0,04*5=1,08, t=5

3.7. Изобразить полученные данные графически

3.8. Дать анализ полученных результатов

Опираясь на полученные данные об уровне рентабельности производства организации с 1993г. по 1999 г. можно сделать следующие выводы:

1. Исходный ряд имеет тенденцию к падению.

2. Средний ежегодный прирост составляет -0,04% при среднем ежегодном уменьшении уровня рентабельности в 0,986 раза, то есть наблюдается падение на 1,4%.

3. На основе произведенных расчетов, методом экстраполяции, можно сделать вывод, что уровень рентабельности в 2000 году составит 1,12%, а в 2001 году составит 1,08%

25