Тема 6: Физические принципы формирования оттенка.

В компьютерной графики имеются 2 вида световых объекта:

1)излучающие

2)несамосветящиеся объекты (отражают, преломляют падающий свет)

Аддитивное формирование оттенка объекта. – самосветящиеся RGB

Сутрактивное – несамосвтящиеся. Вычитание из падающенго света определ длин волн CMY

Цветовая модель позволяет описать необходимый оттенок и необходима для интерполяции.

В КГ чаще всего используются след модели:

1)RGB – аппаратно-ориентированная модель, используемая в ГР для аддитивного формирования2 оттенка самосветящихся объектов. Куб с началом отсчета с центром в системе координат. 00 00 00 – черный, ff ff ff – белый

2)CMY - аппаратно-ориентированная модель, используемая в ГР для субстрактивного формирования оттенка несамосветящихся объектов. Это дополнительные цвета к RGB. Куб с началом отсчета в точке RGB с максимальными значениями. 00 00 00 – белый. При векторном представлении единичный вектор –

3)YIQ - аппаратно-ориентированная модель, используемая в ТВ для сокращения передаваемой полосы частот за счет использования психофизиологических особенностей зрения.

4)HSV – цветовой тон, насыщенность, количество света. Ориентирована на человеческое восприятие и обеспечивающая возможность явного задания требуемого оттенка света. Пространства, определяемое данной схемой – перевернутый шестиугольный конус. Вертикальная ось – светлота(V [0//вершина,1//основание]) . Цветовой тон отсчитывается по контуру конуса(0 – красный, 60 – желтый, 180 – голубой, 240 – синий, 300 – пурпурный, 360 - красный). Насыщенность – определяет насколько оттенок близок к правильному ([0//ось,1//грань]).

5)HLS – цветовой тон, светлота, насыщенность. Ориентирована на человека и настроена на явное задание оттенка. Двойной конус. Черный цвет- вершина нижнего конуса, L=1. Белый свет – вершина верхнего конуса, L=0. Максимальные интенсивные цветовые тона соответствуют основания конусов L =0,5 . H соответствует углу поворота. S задается расстоянием от вертикальной оси до боковой поверхности конуса. Максимальная насыщенность на пересечении вершин конусов.

Тема. Задание цветов для графических устройств.

Используются чаще всего растровые дисплеи, которые используют аппаратно-ориентированную модель цветов RGB. Растровые дисплеи могут быть с таблицей цветности, в которой значение цвета пикселя, заносимого в память, представляет собой индекс в ТЦ. При необходимости отображения пикселя на экране в зависимости от его оттенка выбирается элемент таблицы цветности, содержащий тройку значений RGB.Она передается из видеопамяти на монитор для задания цвета пикселя. (хранится индекс из таблицы цветности)

Для полноценных дисплеев для каждого пикселя в память заносится трока значений RGB. Хранится сама тройка значений.

В модели RGB легко задавать яркость для одного из основных цветов, но затруднительно задавать оттенок с требуемым цветовым тоном и насыщенностью. В ГР для облегчения выбора цветового тона и насыщенности используется палитры цветов. Также используется модели HSV и HSL, которые позволяют непосредственно задать оттенок. Используется иногда интерполяция цветов// для создания эффектов реалистичности изображения.

В ГР интерполяция цветов используется при наложении цветов в технике акварели + при создании эффектов постепенного изменения цвета + построчном заполнении прямоугольников методом Гура.

Если требуется интерполировать между 2 оттенками с одинаковым тоном/насыщенностью, используются HSV/HSL. Основной характеристикой отображающих устройств является пространственное разрешение, которая определяется 1)размером растра; 2)возможностями размещения растра/пятна. Обычно растр/пятно представляет собой определенную область с убыванием интенсивности цвета от центра к краям. Для улучшения качества изображения используется пересечение растров/пятен. Если оно ниже уровня 0,6 от максимальной интенсивности, то растры/пятна различимы. Если выше, то нет. Для повышения качества изображения также используется форма пятна, или распределение яркости по пятну, или адресное разрешение//точность, с которой может задаваться позиция растра/пятна; как правило, больше ил равно пространственному//.

Тема. Генерация векторов.

Назначение генерации векторов – это соединение двух точек изображения отрезком прямой. В ГР чаще используются 4 алгоритма генерации векторов. Два алгоритма ЦДА (цифрового дифференциального анализатора): обычный и несимметричный; алгоритм Брезенхема для генерации векторов; алгоритм Брезенхема для генерации ребер заполненного многоугольника с уменьшением ступенчатости.

Для реализации алгоритма необходимо учитывать общие требования к изображению отрезка:

1)Концы отрезка должны находиться в заданных точках.

2)Отрезки должны выглядеть прямыми.

3)Яркость вдоль отрезка должна быть постоянной и не зависеть от длины и наклона оного.

Ни одно из этих условий не может быть выполнено на растровых устройствах, т.к. концы отрезков могут находиться только на пикселях (целое значение), отрезок аппроксимируется набором пикселей и он может прямым, только если он горизонтальный/вертикальный/под углом 45 в остальных случаях появляется ступенчатость. Яркость для различных отрезков не может быть постоянной. Перечисленные алгоритмы используются для уменьшения отклонений от указанных требований.

ЦДА

Основная задача ЦДА – решение дифференциального уравнения отрезка.

Py, Px – приращения отрезков по Y/X.

От конечного вычитается начальное.

ЦДА формирует дискретную аппроксимацию непрерывного решения данного дифура. Для обычного ЦДА, который чаще используется в векторных устройствах, определяется количество промежуточных точек/узлов. Они используются для аппроксимации кривой. Затем за N циклов вычисляются координаты очередных узлов.

Xi+1 = Xi + Px/N; Yi+1 = Yi + Py/N

Xi & Yi преобразуются в целочисленные значения, который указывают координаты след узла/ путем округления/отбрасывания дробной части.

Недостатки: точки могут прописываться несколько раз, что увеличивает время построения. Также используется операция деления при определении координат. Нельзя выбрать ведущую координату.

Несимметричный ЦДА

Использует ведущую/относительную координату и единичный шаг по относительной координате. Для выбора относительной координаты сравниваются приращения по оси Х и У.

Px > Py : X – ведущая ось; Px < Py : Y - ведущая ось

При выборе следующего узла координата X изменяется на 1 Px раз, а координата Y изменяется столько же, но по формуле Yi+1 = Py/Px .

Если ведущей является Y, то Yi будет меняться на 1, а Xi+1 = Px/Py/

Недостаток этого алгоритма – кол-во узлов аппроксимации должен быть достаточно большим и зачастую равен числу пикселей вдоль наибольшего приращения.

Достоинства – упрощение математических вычислений и исключается повторный расчет точек.

Этапы алгоритма

1)Вычисление приращений координат

2)Определение ведущей координаты

3)открывается цикл по ведущее координате от нач до кон значений

В нем определяются промежуточные координаты : по ведущей координате с добавлением единицы к текущей.

4)рисуется очередной узел и соединяется с предыдущим

Алгоритм Брезенхема

Не требует операции деления, но при этом обеспечивает минимальное отклонение сгенерированного образца от истинного отрезка

Если угловой коэффициент прямой меньше ½ , то следующая точка не меняет своих координат по ведущей оси, а по неведущей меняется на у.е. В ином случае, обе координаты меняют свое значение на у.е.

Используется величина отклонения точной позиции от середины между двумя возможными растровыми точками в направлении наименьшей относительной координаты. Если коэффициент отклонения меньше 0, то значение по y округляются до наименьшего целочисленного, в противном случае увеличивается на 1. Величина отклонения рассчитывается для каждого узла.

E1 = Py/Px - ½

Для последующих узлов величина отклонеия вычисляется след образом

En+1 = En + Py/Px

Py/Px < 0 : Xi+1 = Xi ; Yi+1 = Yi + 1

Py/Px > 0 : Xi+1 = Xi + 1; Yi+1 = Yi

///Пример для ведущего Y;

1)Выбираются начальные значения

2)Определение приращения

//иногда упрощают определение величины E, но при этом снижается качество отображения граней объекта. Вычисляется слуд образом : E = Py*2 – Px // для ведущего Y

3)рисуется первоначальная точка

4)открывается цикл и определяется, что если E больше или равна 0, то к обеим координатам по 1 и определяется величина отклонения для следующей точки. Ei+1 = Ei + 2(Py - Px) // Y leads

Если E < 0 , то 1 добавляется только к неведущей координате. И определяется приращение для текущее координаты.

5)рисуется текущая точка и соединяется с предыдущей.

Алгоритм используется в тех случаях, когда можно выбрать в зависимости от наклона ведущую ось.

Достоинства – упрощаются математические вычисления для определения координат, а в некоторых случаях уходит операция деления. Точки не прорисовываются многократно.

Недостаток – алгоритм за счет дополнительных вычислений и проверок становится более громоздким.

В некоторых ГР данный алгоритм используется в матричной форме.

Тема: Модели расчета освещенности граней 3D объекта.

В компьютерной графике основной характеристикой света является яркость.

Но т.к. она является субъективным понятием, основанным на восприятии человека, то для численных расчетов применяется термин «интенсивность» и рассматривается как яркость и является энергетической характеристикой световой волны. В большинстве ГР интенсивность принимает значение от 0 до 1. Равно 0 при полном отсутствии света, 1 при максимальной яркости.

В КГ для расчета освещенности граней трехмерных объектов используется трехкомпонентная цветовая модель RGB. Интенсивность отраженного света вычисляется отдельно для каждой из цветовых компонент. Затем объединяют в результирующий цвет.

При расчете используют следующие типы освещения и отражения:

1)рассеянное

2)диффузное

3)зеркальное

Освещение граней рассчитывается для каждого типа в отдельности, но если присутствуют несколько типов, то определяется результирующая интенсивность. Рассмотрим интенсивность для всех трех типов отражения.

1)Рассеянное освещение и отражение

Интенсивность считается постоянной в любой точке пространства. Она обусловлена множественными отражениями от всех объектов в пространстве. При освещении объекта рассеянным светом, интенсивность отраженного света определяется по формуле

Ia = Ip * ka, где Ia – интенсивность отраженного света. Ip – интенсивность падающего света. Ka – коэффициент рассеяния, Ka = [0,1].

Чем более матовый материал тем ближе к 0. Зеркальный же ближе к 1.

2)Диффузное

Для расчета интенсивности диффузного отражения света в ГР используется закон косинусов Ламберта. Исходя из него, интенсивность определяется следующим образом.

Kd – коэффициент диффузного отражения

А – угол падения между направлением на источник света и нормалью к поверхности

Ip – интенсивность падающего света

Интенсивность диффузного отражения в большинстве ГР рассчитывается векторным методом. Для этого направление на источник света представлена единичным вектором l, а нормаль к поверхности как единичный вектор n. Тогда cos a = (n * l)//скалярное произведение.

Конечная формула

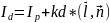
3)Отраженное

Интенсивность отраженного света рассчитывается с помощью различных эмпирических моделей, которые позволяют учитывать шероховатость объекта.

Чаще используется модель Фонга. Интенсивность рассчитывается в зависимости от степени отклонения от истинного значения вектора зеркального отражения луча света. Используется векторный метод. Определяется вектор зеркально-отраженного луча света r и вектор, определяющий направление на наблюдателя, v. , где n – может принимать значение от 1 до 200 , в зависимости от отражающих способностей материала. Большее значение n может соответствовать большей гладкости/зеркальности объекта.

Результирующая интенсивность отраженного света уменьшается обратно-пропорционально квадрату расстояния от источника до наблюдателя и учитывается все виды освещения и отражения.

В некоторых ГР для ускорения вычисления используют не квадрат расстояния, а просто расстояния. Также иногда не учитывается прозрачность материала.

Для расчета интенсивности света для двух перекрывающих поверхностей. И та, что ближе к наблюдателю является полупрозрачной, то результирующая интенсивность. Интенсивность вычисляется по формуле:

A – Коэффициент прозрачности.

Тема: Алгоритмы отсечения невидимых граней.

Для упрощения расчетов используется параметрическое задание прямых. Точка пересечения определяется по формуле x = x1 + t(x1 – x2), y = y1 + t(y1 –y2),где t меняется от 0 до 1, а х1, у1- начало отрезка и х2,у2 – его конец. Специальная проверка требуется тогда, если отрезок параллелен стороне видимой зоны. Если учесть, что координата х точки пересечения найдена, то значение t определяется по формуле t = (x- x1) / (x2 –x1), а y определяется по стандартной формуле, но уже подставляя значение t.

Исопльзуются различные алгоритмы, в том числе с упрощенными вычилениями. Чаще всего используется алгоритм Коэна Сазерлена. Он позволяет легко определить нахождение отрезка полностью внутри/снаружи зоны видимости.

В алгоритме зона видимости разбивается на 9 прямоугольников-подобластей, где каждая из них имеет совой 4битный код.

1001	1000	1010
0001	0000	0010
0101	0100	0110

Первый бит – точка выше окна (ymax - y)

Второй бит – точка ниже окна (xmax - x) // y - ymin

Третий бит – точка справа от окна (x - xmin) // xmax - x

Четвертый бит – точка слева от окна (y - ymin) // x - xmin

Значения битов определяется по знакам операций. Отрезки по алгоритму рисуются без отсечения.

Отрезки, которые не прорисовываются имеют код все 1.

Для повышения качества отображения сцены не применяется последовательное разделение отрезка и прорисовывается видимая его часть.

Работа алгоритма

Просчитываются коды для начала и конца отрезка

Если оба кода равны 0000, то весь отрезок виден и рисуется целиком.

Операция сравнения кодов – бинарный И

Если оба кода равны 1111, то отрезок не виден вообще и отбрасывается

Если 1 или оба кода состоят из 0 и 1, то используется последовательное разделение отрезка. На каждом шаге конечная точка отрезка с ненулевым кодом заменяется на точку, лежащую в поле окна. При этом порядок перебора сторон окна не имеет значения. Эта процедура продолжается до тех пор, пока текущая точка отрезка не получает код 1111.

Используются 2 класса алгоритмов удаления невидимых ребер и граней объекта:

1) Алгоритмы, работающие в пространстве объекта

Для определения видимости грани сравнивается ее положение с остальными гранями в сцене. Кол-во результирующих операций в данном случае N²

2) Алгоритмы, работающие в пространстве сцены//изображения (нахождение точки ближайшей грани, которую пересекает луч зрения. Т.к. луч зрения проходит через все точки растра и кол-во таких точек фиксировано, то алгоритмы этого класса менее чувствительны к увеличению количества объектов в сцене.)

Кол-во операций для построения 3D-сцены будет равным k*N, где k – кол-во точек в растре, N – кол-во ребер/граней.

Алгоритм удаления невидимых граней с использованием Z-буфера

Данный алгоритм является одним из наиболее часто используемых в современных ГР. Он работает в пространстве изображения в параллельной проекции. В качестве Z-буфера используется двумерный массив совпадающий по размерам с окном изображения. В этом массиве хранятся текущие z-координаты каждого пикселя. Первоначально в нем находятся значения, соответствующие бесконечности (самой отдаленной точки сцены). Каждая грань трехмерного объекта представляется в виде многоугольника. И этот многоугольник преобразуется в растровую форму, и для каждой токи многоугольника вычисляется значение z-координаты. И если она меньше чем текущее значение Z-буфера, то в него заносится данная координата. После помещения в растр всех многоугольников, изображение прорисовывается с текущим значением Z-буфера. Следовательно в нем будут хранится только видимые ребра. Этот алгоритм позволяет учитывать координату z и в результате прорисовывать только те грани, которые зафиксированы в Z-буфере.

Алгоритм сортировки в глубину//алгоритм Ньюэлла и Санча.

Этот алгоритм комбинирован между 1 и классом. Т.к. одна его часть работает в пространстве объекта, а другая – в пространстве изображения. Параллельная проекция. Для него используется пространственная оболочка (минимальный прямоугольный параллелипипед, целиком содержащий в себе данный объект).

Алгоритм состоит из 3 основных шагов:

1)упорядочение всех многоугольников в соответствии с их наибольшими z-координатами.

2)разрешение всех неопределенностей, возникающих при перекрытии граней.

3)преобразование каждого из многоугольников в растровую форму, производимое в порядке уменьшения их наибольшей Z-координаты. При этом ближайшие прорисовываются последними.

Для реализации 2 шага используется 5 тестов и принимается следующий алгоритм:

1)Пусть многоугольник P находится в конце после упорядочения, т.е. является самым удаленным

2)Все многоугольники Q, чьи оболочки перекрываются с Z-оболочкой P, должны проходить проверку по 5 тестам. И если на некотором тесте получен утвердительный ответ, то многоугольник P преобразуется в растровую форму. Если во всех 5 тестах получен отрицательный ответ, то многоугольник P, закрывает многоугольник Q. И меняются местами P и Q. Для избегания циклов при переписывании вводится ограничение: многоугольник, перемещенный в конец списка получает метку и не может быть повторно перемещен. Вместо перемещения P и Q разделяются плоскостью нового многоугольника. И алгоритм продолжает работу.

Тесты:

1)X-оболочки многоугольников не перекрываются => сами многоугольники не перекрываются.

2) Y-оболочки многоугольников не перекрываются => сами многоугольники не перекрываются.

3)Многоугольник P полностью расположен с другой стороны от многоугольника Q, который на данный момент находится дальше всего от наблюдателя

4)Многоугольник Q полностью расположен по другую сторону многоугольника P, который является ближайшим к наблюдателю на текущий момент.

5)Проекции многоугольников P и Q на экране не перекрываются //сравнение ребер многоугольников.

Если плоскости перекрывают друг друга в различных зонах, то используя алгоритм сортировки в глубину может привести к зацикливанию, т.к. в одной области проекции плоскость P находится дальше Q от наблюдателя, а в другой части проекции Q находится дальше. В таком случае более сложный многоугольник разбивается на 2 многоугольника.

Дальше от наблюдателя располагается первый отмеченный многоугольник.

Существуют узкоспециализированные АУГ. Обычно их используют для выпуклых тел.

И позволяют производить вычисления намного быстрее. Они работают для центральной перспективной проекции и используются для определенных частей объекта. Они могут работать на небольших частях сцены.

Тема: Кубический сплайн

Сплайны используются для рисования гладких кривых по заданным граничным точкам или для решения задач интерполяции, т.к. через 2 точки можно провести бесконечное кол-во кривых линий, то для решения данной задачи в ГР используются ряд математических сплайнов – это функции, используемые для аппроксимации кривых линий.

Чаще всего используются: 1)кубические сплайны

2)параметрические сплайны

Кубические сплайны – это решения полиномов третьей степени, т.к. с их помощью довольно удобно и просто проводить кривые линии, которые соответствуют человеческому восприятию.

Сплайновую функцию для построения графика функции одной переменной.

Как правило задается последовательность промежуточных точек.

Для построения сплайна необходимо выполнение следующего условия

А также: 1)Заданная функция должна проходить через все заданные точки.

2)Данная функция должна быть дважды непрерывно дифференцируема на всем отрезке.

Математически кубический сплайн – это на каждом отрезке прямой вычисляется ф-цие в виде полинома третьей степени.

Основная задача для данной функции сводится к нахождению коэффициентов, т.к. для каждого отрезка необходимо найти по 4 коэффициента.

Для рисования КС в ГР используется решение системы 3 уравнений для оси X, Y и Z.

В ГР для заданий КС используют начальные точки и вектор-касательную к ним. Подобное упрощение приводит к параметрическим сплайнам, которые чаще всего реализуются двумя формами: Эрмита и Безье.

Форма Эрмита предполагает задание сплайна начальной и конечной точками и векторов-касательных к ним. В данном случае решается задача нахождения четверки коэффициентов. И если обозначить конечные точки P1, P2, а вектора-касательные r1, r2, то условия для построения сплайна для заданных точек будет выглядеть следующим образом:

1)Для начальной точки

Для решения используют матричную форму:

Аналогично и для других координат.

Для определения P1x, P2x, r1x, r2x используют векторно-матричное уравнение

В ГР кривые по форме Эрмита рисуются в зависимости от значений r1 и r2.

Форма Безье

Форма Безье задается начальной и конечной точкой кривой и радиус-вектором. Направление и величина указывает выпуклость кривой. При использовании формулы Безье рисуется четырехугольник с параметрами

Величина P0 = 3(P3 – P4); P1 = 3(P4 – P2). Графическое построение кривой линии используя форму Безье, в ГР реализуется параметрическим сплайном формы Безье. В зависимости от сложности кривой в ГР можно скомбинировать форму Эрмита и форму Безье или перейти от одной к другой.

Тема: Модели освещения в ГР.

В ГР для построения реалистичных изображений и освещения используется специальные математические модели. Они основаны на теории, эвристических наблюдениях и на умозрительных заключениях. Чаще всего в ГР используется простая МО и глобальная МО.

Простая МО основана на принципе – любой объект, находящийся в сцене можно увидеть только в одном из 3 случаев:

1) Объект излучает свет

2) Объект отражает свет

3) Прозрачный или полупрозрачный объект пропускают свет

Данная модель считает, что если объект поглощает весь падающий на него свет, то он выглядит абсолютно черным. И если объект не поглощает падающий свет, то он выглядит белым. И если он поглощает только часть спектра, то он цветной. В данной модели используются только диффузной и зеркальное отражение. Эти два вида отражения можно комбинировать в разных пропорциях и зависят от материала объекта. Интенсивность диффузного света зависит и от расстояния от источника до поверхности. Зеркальное отражение используется только для чистых зеркал. Если шероховатость поверхности больше чем у чистого зеркала, то используется диффузное отражение.

Глобальная модель освещения = Модель трассировки луча.

ГМО учитывает такие эффекты, как отражение, прозрачность, полупрозрачность, тени, текстуры. Эти эффекты можно реализовать при помощи алгоритма трассировки луча. Он также позволяет удалять из сцены невидимые поверхности. Отслеживаются//трассируются лучи, выходящие из камеры и проходящие через каждый пиксель сцены. Пиксель окрашивается в тот цвет через который проходит луч. Если луч не пересекает пиксель, то он окрашивается в черный. Трассировка начинается из глубины сцены. Качество сцены учитывается диффузное и зеркальное отражение. Если точка закрыта от источника света другим объектом, то она находится в полной тени и ее яркость равна яркости рассеянного света в данной сцене. Освещение ослабляется при прохождение через прозрачные и полупрозрачные объекты и может даже изменить оттенок освещения.

Некоторые ГР используют усложненный алгоритм трассировки луча. Каждый луч попадающий на объект делится на 2 луча: отраженный и преломленный. Трассировка прекращается при покидании лучом сцены или при падении его интенсивности до определенного предела. Когда все лучи отслежены, вычисляется суммарный цвет пикселя.

Отследив все лучи, получаем полную проекцию схемы с учетом отражений, прозрачности, теней.

Тема: Эффекты, используемые в ГР.

1)Прозрачность

При рассмотрении прозрачности сталкиваемся с таким явлением, как преломление при переходе от одной среды к другой. В ГР преломление рассчитывается по закону Снелиуса.

M1 sin a = m2 sin b. M1, M2 – коэффициенты преломления сред. A – угол падения, b – угол преломления. В ГР ни одно вещество не пропускает весь падающий свет, часть его всегда отражается. Пропускание может быть направленным и диффузным. Направленное пропускание свойственно прозрачным веществам. Диффузное свойственно полупрозрачным или матовым веществам. Полную модель прозрачности можно реализовать только в глобальной МО.

2)Тень.

Тень состоит из 2 частей: полутени и полной тени. Полная тень – это центральная, четкая, темная, резко очерченная часть. Полутень – это более светлая часть.

Тени могут использоваться по отдельности и вместе.

3)Текстуры

В компьютерной графике текстурой называется детализация строения поверхности. Нанесение текстуры на объект позволяет придать вид реальных плоских или объемных поверхностей объекта. Обычная модель освещения реализует только плоские текстуры. Глобальная модель освещения реализует плоские и объемные текстуры. Используется 2 вида нанесения текстур.

1)На гладкую поверхность наносится заранее подготовленный узор.

2)Поверхность объекта предварительно подводится под необходимую шероховатость заранее подготовленного рисунка. Затем наносится рисунок. Этот вид детализации намного сложнее в реализации, т.к. необходимо совместить рельефность поверхности с рисунком.

Нанесение текстуры усложняется при натягивании их на неплоские поверхности. Также возникают проблемы из-за лестничного эффекта, при большом увеличении объекта становится видна зернистая поверхность. Для избегания данной проблемы при нанесении текстуры применяется текстуры больших размеров. Для использования мелких рисунков в качестве текстуры в ГР используются фракталы. Фрактал – геометрическая фигура(тело), части которых являются копией других объектов. Для фрактальных объектов характерно и бесконечное увеличение и можно значительно увеличить степень их детализации.

Лестничный эффект возникает только на растровых сценах. Лестничный эффект сильно заметен на прямых линиях. В КГ для устранения лестничного эффекта используется принцип многоугольников. Пиксели, находящиеся на пересечении двух одинаково окрашенных областей окрашивается в тот же цвет, но темнее. При пересечении объектов разных цветов граничные пиксели окрашиваются в смесь двух оттенков и уменьшается яркость. Только для глобальной модели освещения. Мат.аппарат для реализации алгоритма : лучи посылаются на сцену. Если цвета в вершинах совпадают, то он не находится на грани двух областей. Если цвета различны, то луч проходящий через пиксель разбивается на 4 части и процесс повторяется. Дробление происходит до тех пор, пока разница цветов не будет минимальна.