
- •1. Введение
- •2.Физические основы пластической деформации
- •2.1. Строениие металлов
- •2.2. Механизмы пластической деформации
- •2.3.Упрочнение при пластической деформации
- •2.4. Фазовые превращения при деформации
- •2.5. Нагрев и разупрочнение деформируемых металлов
- •2.6. Пластическая деформация при различных температурно-скоростных условиях
- •2.7.Пластическая деформация при растяжении образца
- •2.8. Влияние температуры, скорости и степени деформации на сопротивление деформации
- •2.9. Контактное трение
- •3. Теория напряжений
- •3.1. Напряжения в данной точке
- •3.2. Тензор напряжений.
- •3.3. Напряжения на наклонной площадке
- •3.4. Главные напряжения. Инварианты тензора напряжений
- •3.5.Эллипсоид напряжений
- •3.6.Главные касательные напряжения
- •3.7.Шаровой тензор и девиатор напряжений
- •3.8. Октаэдрические напряжения
- •3.9.Условие равновесия для объемного напряженного состояния
- •4. Теория деформаций
- •4.1. Перемещение точки при пластической деформации
- •4.2. Деформации в элементарном объеме
- •4.3. Деформации по произвольному направлению. Главные деформации. Инварианты деформаций.
- •4.4. Шаровой тензор деформации, девиатор деформации
- •4.5. Неразрывность деформации
- •4.6. Скорости перемещений и скорости деформаций
- •4.7. Условие постоянства объема
- •4.8. Механические схемы деформаций
- •5. Обобщенный закон упругости
- •5.1. Связь деформаций и напряжений для пространственного напряженного состояния
- •5.2. Связь напряжений и деформаций для пространственного напряженного состояния
- •5.3. Закон упругого изменения объема и закон упругого изменеия формы
- •5.4. Связь между напряжениями и деформациями в пластической области
- •6. Условия перехода деформируемого тела в пластическое состояние
- •6.1. Гипотезы наступления пластической деформации
- •6.2. Влияние среднего по величине главного напряжения на условие пластичности
- •6.3. Частные случаи теории пластичности
- •7. Методы определения усилий и деформаций при обработке металлов давлением
- •7.1. Метод линий скольжения
- •6.2. Решение с применением точных уравнений равновесия и условия пластичности
- •7.3. Решение с применением приближенных уравнений равновесия и условия пластичности
- •6.4.Метод баланса работ
- •7.5.Вариационные методы
6.2. Решение с применением точных уравнений равновесия и условия пластичности
Рассматривается процесс плоской деформации, осадка полосы на шероховатых плитах, рис.7.7.
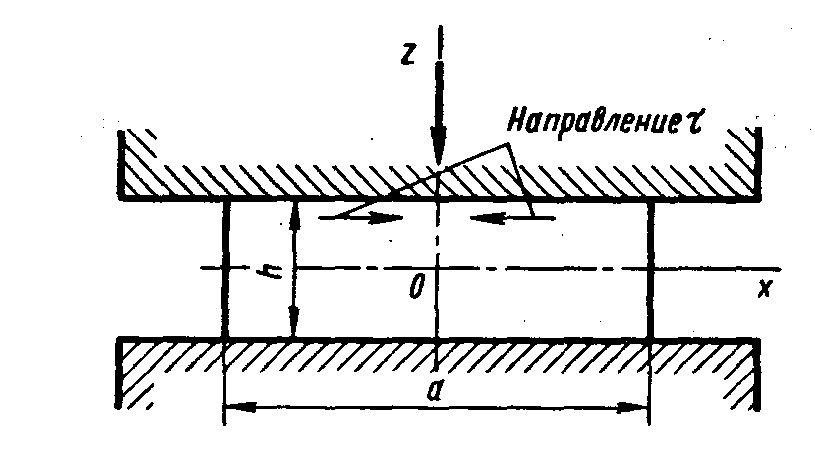
Рис.7.7. Осадка полосы на шероховатых плитах.
Имеем
![]() ;
;
![]() .
.
Систему уравнений можно представить в виде одного уравнения, которое называется обобщенным уравнением равновесия, т.е.
![]() .
.
Уравнение с одним
неизвестным. Упрощенный вариант решения,
когда
![]() зависит
только от координаты
,
тогда
зависит
только от координаты
,
тогда
![]() .
В этом случае
.
В этом случае
![]() .
Решение имеет вид
.
Решение имеет вид
![]() При
При
![]() ,
,
![]() ,
тогда
,
тогда
![]() ,
для
получим
,
для
получим
![]() .
.
С учетом дифференцирования и подстановки в уравнения равновесия
![]() ;
;
![]() .
.
Решая эти уравнения,
запишем
![]() ;
;
![]() ,
,
где
![]() и
и
![]() - произвольные функции. Для их определения
используем условие пластичности, тогда
- произвольные функции. Для их определения
используем условие пластичности, тогда
![]() ;
;
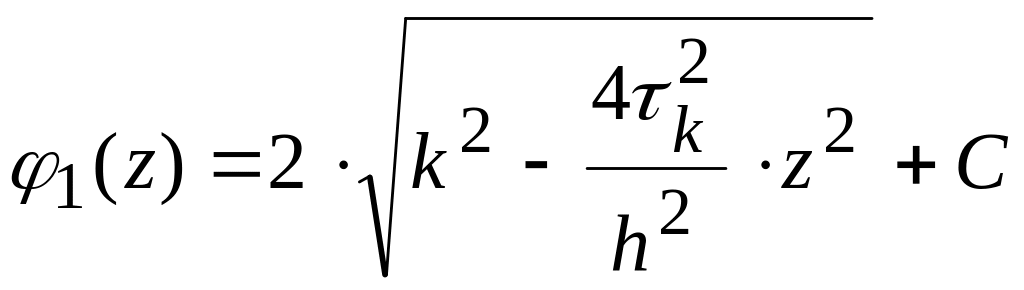 .
.
Подставляя значение произвольных функций, имеем
![]()
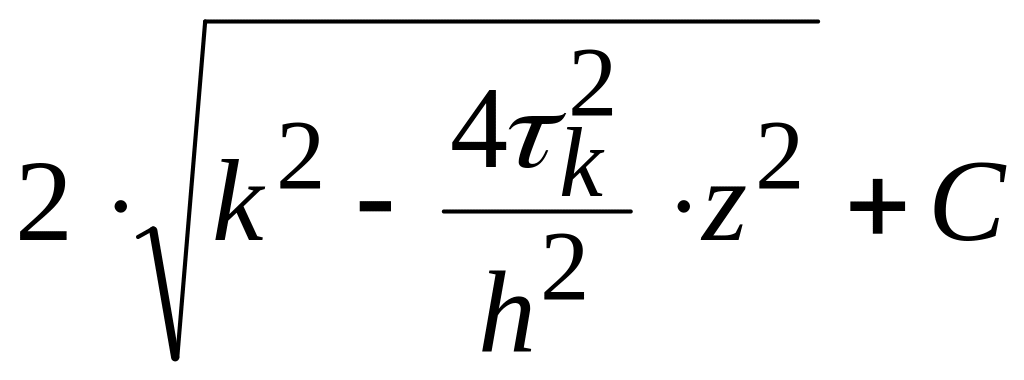 ;
;
![]() ;
.
;
.
Для практического
использования пригодно лишь одно второе
уравнение системы, пренебрегая остальными,
что связано с невозможностью удовлетворения
граничных условий на краю заготовки.
При отсутствии трения напряжение
оставалось бы постоянным, тогда при
![]() ,
,
![]() ,
отсюда
,
отсюда
![]() ;
;
![]() .
.
На контакте
![]() ,
которое по Зибелю
,
которое по Зибелю
![]() .
Подставляя, найдем
.
Подставляя, найдем
![]() .
На рис.7.8 представлено
распределение нормальных напряжений
на контактной поверхности.
.
На рис.7.8 представлено
распределение нормальных напряжений
на контактной поверхности.
Удельное усилие определяется выражением
![]() .
.
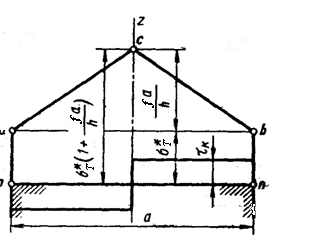
Рис.7.8. Распределение нормальных напряжений на контакте.
Анализ выражения
показывает, что контактное напряжение
кроме предела текучести зависит от
коэффициента трения и фактора формы
![]() .
.
7.3. Решение с применением приближенных уравнений равновесия и условия пластичности
Распределение
нормальных напряжений ищется только
на контактной поверхности. Нормальные
напряжения не зависят от координаты
.
Следовательно,
![]() и
и
![]() .
Принимая напряжения
от
координаты
в
виде линейной зависимости, имеем
.
Принимая напряжения
от
координаты
в
виде линейной зависимости, имеем
![]() .
Подставляя в первое уравнение равновесия,
получим
.
Подставляя в первое уравнение равновесия,
получим
![]() ,
которое и есть приближенное уравнение
равновесия. Принимая условие пластичности
в упрощенном виде
,
которое и есть приближенное уравнение
равновесия. Принимая условие пластичности
в упрощенном виде
![]() и распределение касательных напряжений
на контакте
и распределение касательных напряжений
на контакте
![]() ,
после подстановки и интегрирования,
имеем
,
после подстановки и интегрирования,
имеем
![]() .
.
С учетом граничных
условий
![]() .
Использование закона Амонтона в качестве
граничных условий приводит к новым
выражениям по сравнению с законом
Зибеля. Это свидетельствует о большом
влиянии в решении и на практике
контактного трения в процессах ОМД.
.
Использование закона Амонтона в качестве
граничных условий приводит к новым
выражениям по сравнению с законом
Зибеля. Это свидетельствует о большом
влиянии в решении и на практике
контактного трения в процессах ОМД.
6.4.Метод баланса работ
Метод основан на
законе сохранения энергии. При
пластической деформации работа внешних
сил равна работе внутренних сил на
соответствующих перемещениях:
![]() ,
,
![]() ,
тогда
,
тогда
![]() ,
,
где
![]() -
работа активных сил;
-
работа активных сил;
![]() -
работа сил трения на контакте.
-
работа сил трения на контакте.
Определим приращение
работы внутренних сил элементарного
объема при малой деформации, которое
можно представить, как скалярное
произведение вектора напряжения
и вектора элементарного перемещения
![]()
![]() .
.
При этом
,
.
Учитывая, что скалярные произведения единичных векторов
![]() ,
,
![]() ,
,
можно записать
![]() .
.
Для главных
направлений
![]() .
.
Если напряженное
и деформированное состояние точки
определяется тензором напряжений и
деформаций
![]() и
,
то согласно правилам произведения
матриц получим тот же результат
и
,
то согласно правилам произведения
матриц получим тот же результат
![]()
![]() .
.
Подставляя значения деформаций
![]() Или
Или
![]() .
.
С учетом модуля
сдвига, получим
![]() .
Следовательно
.
Следовательно
![]() .
.
Элементарную
работу внешних сил можно представить,
как скалярное произведение векторов
![]() и
и
![]() .
.
На контакте поверхностные силы и перемещения можно записать в виде
![]() ,
,
![]() ,
,
тогда
![]() .
.
Работа внешних (поверхностных) сил, включая работу контактных сил трения
![]() ,
,
где - проекции сил на оси координат; - перемещения вдоль координат. Работа сил контактного трения
![]() .
.
Работа активных
сил
![]() .
.
Во многих случаях
![]() ,
тогда
,
тогда
![]() .
.
Определим усилие
![]() ,
необходимое для горячей осадки
цилиндрической заготовки диаметром
,
необходимое для горячей осадки
цилиндрической заготовки диаметром
![]() и высотой
и высотой
![]() .
Напряженное состояние осесимметричное.
Используем цилиндрические координаты.
Деформация однородная
.
Напряженное состояние осесимметричное.
Используем цилиндрические координаты.
Деформация однородная
![]() ,
касательное напряжение постоянно на
контактной поверхности
.
Элементарный объем
,
касательное напряжение постоянно на
контактной поверхности
.
Элементарный объем
![]() .
Работа деформации
.
Работа деформации
![]() .
.
Элементарная
поверхность
![]() .
Работа сил трения
.
Работа сил трения
![]() .
.
Для определения
и
![]() в условие постоянства объема подставим
деформации
в условие постоянства объема подставим
деформации
![]() и
,
имеем
и
,
имеем
![]() .
В силу условия однородности
.
В силу условия однородности
![]() .
.
С учетом последнего
![]() .
После интегрирования
.
После интегрирования
![]() .
С учетом очевидных условий
.
С учетом очевидных условий
![]() .
Деформации
.
Деформации
![]() ;
;
![]() .
Интенсивность деформаций
.
Интенсивность деформаций
![]() .
Используя найденные величины, получаем
.
Используя найденные величины, получаем
![]() .
.
После интегрирования
![]() .
Удельное усилие деформирования
.
Удельное усилие деформирования
![]() .
.
Сопоставляя с решением плоской задачи при тех же граничных условиях видно, что при осесимметричном напряженном состоянии удельные контактные силы меньше. Это объясняется присутствием поперечной деформации .
