7.1. Метод линий скольжения
Зная траекторию главных касательных напряжений (диагональные площадки) можно определить напряженное состояние пластически деформируемого тела. Эти траектории или линии скольжения Людерса-Чернова появляются на поверхности деформируемого металла.
На плоскости
в теле, находящегося в плоском деформируемом
состоянии, определим точку
,
рис.7.1, и отложим вектор
главного касательного напряжения.
Перейдем в направлении этого вектора
к точке
и отложим вектор
главного касательного напряжения в
этой точке. Построим ломаную линию
и т.д.
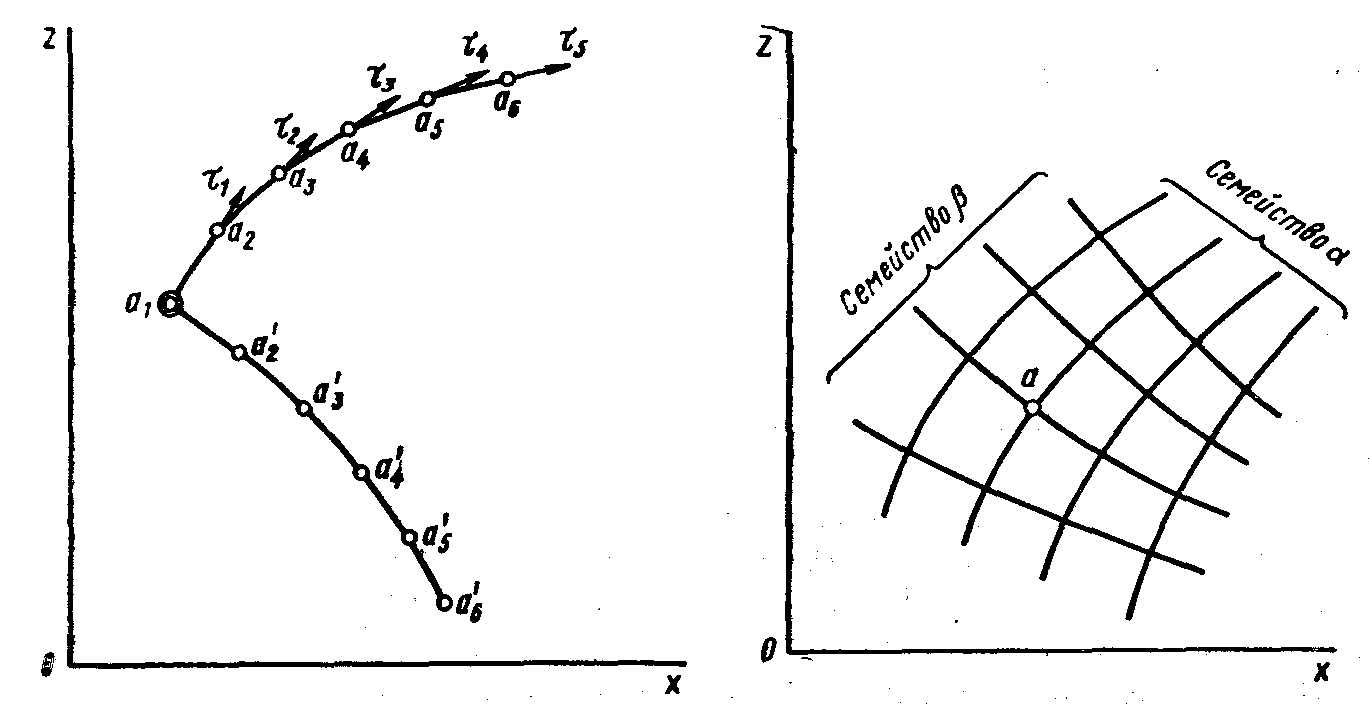
Рис.7.1. Траектории главных касательных напряжений
Вследствие парности
касательных напряжений можно отложить
второй вектор
перпендикулярный к ранее отложенному,
и построить вторую ломаную линию
.
В точке
линии пересекаются под прямым углом.
При увеличении точек ломаные линии
превращаются в плавные кривые семейств
и
,
рис.7.2.
Для разных напряженных состояний поля линий скольжения различны и каждому определенному напряженному состоянию соответствует определенное поле линий скольжения. Имеем две системы линий скольжения, касательные к которым совпадают с направлениями наибольших касательных напряжений.
Обозначим линии скольжения первого и второго семейств соответственно
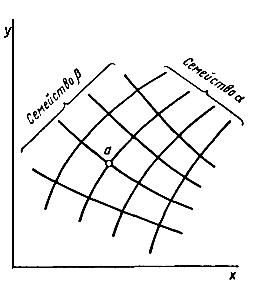
Рис.7.2. Ортогональное поле линий скольжения семейства и
через
и
.
На рис.7.3 и рис.7.4 представлены линии
скольжения и напряжения, действующие
на элементарный треугольник. Максимальное
касательное напряжение достигает
величины
,
т.е. сопротивления пластической деформации
на сдвиг. Нормальное напряжение
на диагональной площадке
.
Спроектируем все силы на нормаль
,
или
.
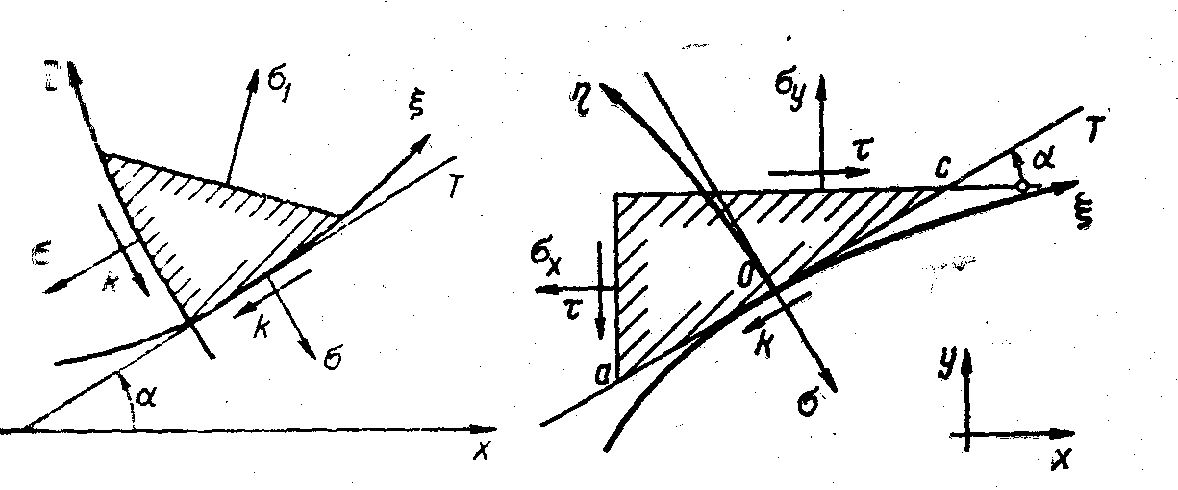
Рис. 7.3. Равновесие элементарного треугольника
Произведем замену
.
Подставляя, получим
.
Учитывая, что
,
запишем
.
Спроектируем все силы на ось , тогда
,
или
.
С учетом подстановки, имеем
.
Рассмотрим
равновесие треугольника
,
рис.6.4, образованного линиями скольжения
и
.
Спроектируем все
силы на ось
,
отсюда
,
с учетом выражения для среднего напряжения
.
Полученные значения компонентов тензора напряжений тождественно удовлетворяют условие пластичности.
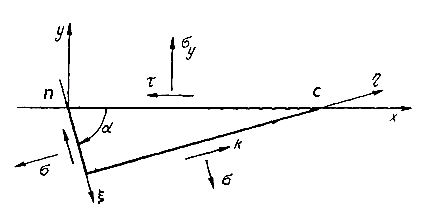
Рис.7.4. Равновесие треугольника .
Рассмотрим уравнения равновесия с учетом последних выражений. Подставляя в дифференциальные уравнения, получим
;
.
Перейдем в уравнениях
к криволинейной системе координат
и
,
где в качестве координат сетки примем
сетку линий скольжения. В этом случае
угол
равен нулю. Так как уравнения справедливы
при любой системе отсчета, имеем
Уравнения равновесия, примут вид
,
или
.
Интегрируя по и по , получим
.
Последние уравнения носят названия интегралов Генки. Если бы положение линий скольжений и было известно, то интегралы Генки представляли бы общее решение задачи о плоской деформации при отсутствии упрочнения.
Пусть в точке
данной
линии скольжения напряжение
и
,
в другой точке
той же линии
и
.
Подставляя в первое уравнение системы
;
.
Так как при перемещении вдоль одной линии скольжения произвольная функция не изменяется, то
,
.
.
Обозначая
,
где
-
представляет угол поворота линии
скольжения при переходе от одной точки
к другой, т.е.
.
Выражение показывает, что изменение пропорционально углу поворота линий скольжения. Если известно положение линий скольжения , то можно определить напряжения в любой точке при известных граничных условий.
СВОЙСТВА ЛИНИЙ СКОЛЬЖЕНИЯ
Свойства линий скольжения сводятся к формулировкам теорем Генки и их дальнейших интерпретаций. Для простейших случаев, используя свойства линий скольжения можно определить их положение и, следовательно, рассчитать, напряженное состояние деформированного тела. Свойства линий скольжения
Линии скольжения непрерывны.
Линии скольжения образуют два семейства.
Семейства линий скольжения взаимно ортогональны.
Линии скольжения пересекают траектории главных напряжений под углом
.Изменение среднего нормального напряжения при движении вдоль линии скольжения пропорционально углу ее поворота.
Угол между касательными к двум линиям скольжения одного семейства в точках пересечения их линиями другого семейства остается постоянным.
Радиусы кривизны линий скольжения изменяются на величину расстояний, пройденных по линиям скольжения другого семейства.
Углы наклона линий скольжения при выходе на контур зависят от величины касательного напряжения на контуре.
ВИДЫ ПОЛЕЙ СКОЛЬЖЕНИЯ
Рассмотрим некоторые виды полей линий скольжения. Линии скольжения представляют систему прямых взаимно перпендикулярных линий. Отсутствие углов поворота определяют постоянство среднего нормального напряжения. У прямолинейной свободной поверхности полем линий скольжения является сетка ортогональных прямых. Это поле равномерного напряженного состояния.
Одно семейство линий скольжения – прямые, другое – кривые, взаимноортогональные. Центрированное поле, образуемое пучком прямых и концентрированных окружностей. Центр поля – особая точка. Такие поля называются простыми. К полю равномерного напряженного состояния может примыкать только простое поле.
В общем случае, поля линий скольжения образуются криволинейными ортогональными линиями. Циклоиды, логарифмические спирали и т.д. При построении комбинируют поля.
ПОЛЕ СКОРОСТЕЙ
Поля скоростей дают возможность определять направление перемещений и судить о характере деформированного состояния. Выведем уравнения, которым должны удовлетворять скорости перемещений вдоль линий скольжения. Выразим компоненты вектора скорости через другие компоненты по направлениям произвольной пары пересекающихся линий скольжения, рис.7.6. Можно показать
;
;
;
.
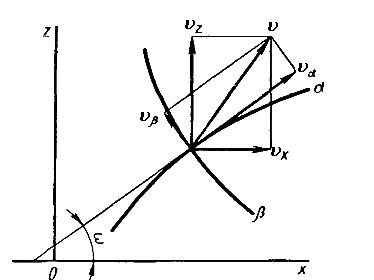
Рис.7.5. Составляющие вектора скорости
Дифференцируя по направлениям дуг систем и
.
С учетом соотношений
;
;
.
Подставляя, имеем
.
На основании
второго уравнения
.
С учетом условия постоянства объема получим
;
.
Из этих выражений получим искомые уравнения, которым должны удовлетворять скорости перемещений вдоль линий скольжения:
(вдоль
);
(вдоль
).
Это уравнения Г.Гейрингер. Это уравнения неразрывности и отражают, что скорости линейных деформаций вдоль линий скольжения равны нулю. В простых полях линий скольжения компоненты скоростей вдоль каждой из прямых линий скольжения постоянны. С помощью уравнений Г.Гейрингер можно построить план скоростей по известному полю линий скольжения.
ПЛОСКОЕ КОЛЬЦО, НАГРУЖЕННОЕ ПО ВНУТРЕННЕМУ КОНТУРУ РАСПРЕДЕЛЕННОЙ РАСТЯГИВАЮЩЕЙ НАГРУЗКОЙ
Деформация
принимается плоской. Определить
величину
,
при которой все кольцо находится в
состоянии пластической деформации.
Отсутствие касательных напряжений
определяет нормальные напряжения
и
,
как главные. Поэтому траектории главных
напряжений представляют собой сетку
окружностей и ортогональных к ним
радиусов, рис.7.6.
Линии скольжения наклонены к траекториям главных напряжений под углом 45о . Этим условиям отвечает логарифмическая спираль. Уравнение логарифмической спирали
,
где - внутренний радиус кольца. Логарифмируя, получим
.
Принимая
.
Тогда
.
Так как точка
лежит на свободной поверхности, то
.
Из условия пластичности, учитывая, что
напряжения
растягивающие, а
сжимающее, имеем
,
откуда
.
Рис.7.6. Траектории главных напряжений линий скольжения
Следовательно,
.
Тогда
,
но
.
С учетом условия пластичности
,
поэтому
,
откуда
.
Задача решена. Получено замкнутое решение для определения усилия и построено поле линий скольжения.
Для данного случая можно получить удельное усилие, решая уравнение равновесия совместно с условием пластичности. Действительно имеем
.
Интегрируя, и
подставляя граничные условия, получим
.
Для внутренней границы . Получен тот же результат, что и при решении задачи методом линий скольжения.