6. Условия перехода деформируемого тела в пластическое состояние
Критерий, который определяет условия возникновения пластической деформации при сложном напряженном состоянии, называется условием пластичности.
6.1. Гипотезы наступления пластической деформации
ПЕРВОЕ ПРЕДЕЛЬНОЕ СОСТОЯНИЕ
Рассмотрим одноосное
напряженное состояние, в этом случае
имеем нормальное растягивающее напряжение
.
На рис. 6.1 представлена схема напряжений,
действующих на наклонной площадке
растягиваемого образца. Напряжения
растяжения
,
Напряжение на наклонной площадке
,
при этом
,
,
.
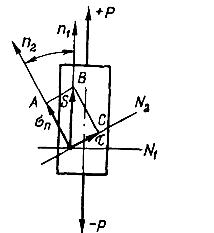
Рис.6.1. Схема напряжений, действующих на наклонной площадке
Аналогичные формулы можно получить, используя выражения для нормальных и касательных напряжений на наклонной площадке при .
Действительно,
,
,
.
,
,
=
.
т.к.
,
,
тогда
Пластическая
деформация реализуется под действием
максимальных касательных напряжений,
т.е. при максимальном значении
тригонометрической функции и максимальном
значении напряжения
,
тогда
,
или
.
Последняя формула представляет первое предельное состояние при линейном напряженном состоянии.
Первое предельное состояние позволяет установить подходы реализации условия пластичности для объемного напряженного состояния, воспользовавшись гипотезой «единой кривой». В этом случае предполагается независимость вида уравнений от схемы напряженного состояния. В последнем выражении, с одной стороны предел текучести , зависящий от деформационных, скоростных и температурных факторов. С другой, величина, характеризующая напряженное состояние точки, в данном случае .
Гипотеза «единой кривой» позволяет поставить знак равенства между значениями, характеризующие объемное напряженное состояние и пределом текучести, полученного на основании опытных данных в условиях линейного растяжения или сжатия.
УСЛОВИЕ ПЛАСТИЧНОСТИ ТРЕСКА - СЕН-ВЕНАНА ИЛИ ГИПОТЕЗА МАКСИМАЛЬНЫХ КАСАТЕЛЬНЫХ НАПРЯЖЕНИЙ
При объемном
напряженном состоянии, кроме главного
напряжения
присутствуют еще напряжения,
и
.
Какое сочетание
главных напряжений определяет напряженное
состояние точки? В общем, для определения
условия пластичности, необходимо знать
зависимость
.
Принимая положение о наступлении пластической деформации под действием максимальных касательных напряжений, следует рассмотреть напряжения на диагональных площадках, на которых касательные напряжения получают экстремальное значение и имеют вид
.
Записывая
соотношения
,
имеем максимальную разность и максимальные
касательные напряжения
.
Выше было показано,
что при линейном напряженном состоянии,
когда
,
.
Используя гипотезу
«единой кривой»,запишем
или
.
Условие пластичности Треска – Сен-Венана. Принципиальным отличием от условия первого предельного состояния заключается в том, что напряженное состояние точки определяется разностью главных нормальных напряжений, а не величиной одного главного напряжения .
В общем случае, напряженное состояние тела неоднородно, отсюда условие пластичности применяют для каждой точки деформируемой среды. Поэтому максимальные разности для отдельных точек могут меняться, тогда
,
,
.
Условие Треска –
Сен-Венана имеет, в данной форме, наглядную
геометрическую интерпретацию в
координатах
Фигура представляет собой правильную
шестигранную призму, ось которой проходит
через начало координат, одинаково
наклоненной к координатным направлениям.
Поверхность призмы называется поверхностью
пластичности. Если напряженное состояние
определяется точкой расположенной
внутри призмы пластичности, то тело
находится в упругом состоянии, если на
поверхности - тело находится в пластическом
состоянии. Вне пределов призмы – смысла
нет. Сечение поверхности пластичности
плоскостью
показано на рис.6.2.
Характерные точки
- переход в предельное состояние при
одноосном растяжении (сжатии). Точки
- переход в предельное состояние при
двухосном растяжении (сжатии).
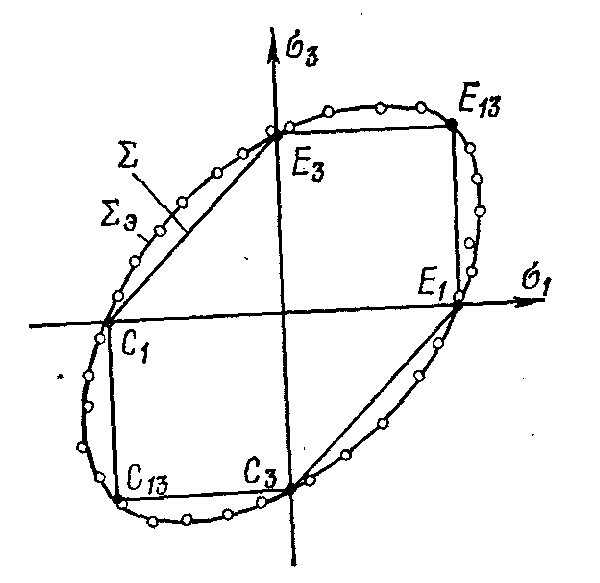
Рис.6.2. Сечение поверхности пластичности
УСЛОВИЕ ПЛАСТИЧНОСТИ ГУБЕРА-МИЗЕСА
Недостатком условия пластичности Треска - Сен-Венана является отсутствие учета в напряженном состоянии точки среднего главного напряжения .
Обобщенной
характеристикой напряженного состояния
можно считать октаэдрическое касательное
напряжение
,
с учетом запишем
.
При линейном
напряженном состоянии, с учетом первого
предельного состояния, октаэдрическое
касательное напряжение равно
.
Воспользуемся
гипотезой «единой кривой», Тогда
=
,
или
=
.
В левой части
интенсивность касательных напряжений
в главных координатах, т.е.
.
В произвольных координатах
.
Последние три равенства представляют собой условие пластичности Губера-Мизеса, которое формулируется следующим образом: предельное состояние пластичности наступит тогда, когда интенсивность напряжений при объемном напряженном состоянии достигнет предела текучести. При имеем , т.е. переходим к первому предельному состоянию в условиях линейного напряженного состояния .
Условие Губера-Мизеса в литературе имеет несколько наименований:
- условие постоянства интенсивности напряжений;
- условие постоянства октаэдрического касательного напряжения;
- условие постоянства удельной энергии изменения формы или «энергетическое условие».
Условие Губера-Мизеса
имеет геометрическую интерпретацию.
Поверхность пластичности отображается
цилиндрической поверхностью, ось которой
одинаково наклонена к направлениям
Сечение
поверхности пластичности плоскостью
,
называется контуром пластичности и
имеет вид эллипса, рис.5.2. В точках
условие пластичности Губера-Мизеса и
Треска - Сен-Венана дают одинаковый
результат. Представляет интерес
определение напряжений
,
и
таким образом, чтобы они удовлетворяли
условие пластичности. Показано, что
главные напряжения могут тождественно
удовлетворить уравнение пластичности
при условии
,
,
-
угол вида напряженного состояния. Подставляя
напряжения в условия пластичности,
получим тождество.