
- •1. Введение
- •2.Физические основы пластической деформации
- •2.1. Строениие металлов
- •2.2. Механизмы пластической деформации
- •2.3.Упрочнение при пластической деформации
- •2.4. Фазовые превращения при деформации
- •2.5. Нагрев и разупрочнение деформируемых металлов
- •2.6. Пластическая деформация при различных температурно-скоростных условиях
- •2.7.Пластическая деформация при растяжении образца
- •2.8. Влияние температуры, скорости и степени деформации на сопротивление деформации
- •2.9. Контактное трение
- •3. Теория напряжений
- •3.1. Напряжения в данной точке
- •3.2. Тензор напряжений.
- •3.3. Напряжения на наклонной площадке
- •3.4. Главные напряжения. Инварианты тензора напряжений
- •3.5.Эллипсоид напряжений
- •3.6.Главные касательные напряжения
- •3.7.Шаровой тензор и девиатор напряжений
- •3.8. Октаэдрические напряжения
- •3.9.Условие равновесия для объемного напряженного состояния
- •4. Теория деформаций
- •4.1. Перемещение точки при пластической деформации
- •4.2. Деформации в элементарном объеме
- •4.3. Деформации по произвольному направлению. Главные деформации. Инварианты деформаций.
- •4.4. Шаровой тензор деформации, девиатор деформации
- •4.5. Неразрывность деформации
- •4.6. Скорости перемещений и скорости деформаций
- •4.7. Условие постоянства объема
- •4.8. Механические схемы деформаций
- •5. Обобщенный закон упругости
- •5.1. Связь деформаций и напряжений для пространственного напряженного состояния
- •5.2. Связь напряжений и деформаций для пространственного напряженного состояния
- •5.3. Закон упругого изменения объема и закон упругого изменеия формы
- •5.4. Связь между напряжениями и деформациями в пластической области
- •6. Условия перехода деформируемого тела в пластическое состояние
- •6.1. Гипотезы наступления пластической деформации
- •6.2. Влияние среднего по величине главного напряжения на условие пластичности
- •6.3. Частные случаи теории пластичности
- •7. Методы определения усилий и деформаций при обработке металлов давлением
- •7.1. Метод линий скольжения
- •6.2. Решение с применением точных уравнений равновесия и условия пластичности
- •7.3. Решение с применением приближенных уравнений равновесия и условия пластичности
- •6.4.Метод баланса работ
- •7.5.Вариационные методы
4. Теория деформаций
4.1. Перемещение точки при пластической деформации
Рассматриваются
малые пластические деформации, т.е.
деформации в данный момент времени. При
деформации каждая точка смещается
относительно первоначального своего
положения. Пусть перемещение точки в
пространстве определяется вектором
![]() .
Его составляющие
.
Его составляющие
![]() ,
тогда
,
тогда
![]() ,
,
где 1,2,3 – направления разложения вектора согласно правилу параллелепипеда.
Если элементарный объем повернуть относительно осей 1,2,3, то составляющие относительно новых граней будут располагаться произвольным образом и тогда каждую из них можно разложить по правилу параллелепипеда на составляющие вдоль произвольных координат , рис.4.1.
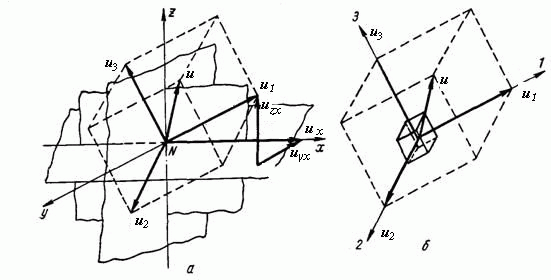
Рис.4.1. Перемещение материальной точки
В этом случае векторная сумма
![]() .
.
Каждая тройка перемещений соответствует одной площадке, т.е.
![]() ;
;
![]() ;
;
![]() .
.
Касательные составляющие равны нулю, тогда
![]() ;
;
![]() ;
;
![]() ,
,
т.е. нормальные составляющие перемещений достигают экстремального значения. Направление оси определяется единичным вектором , оси - вектором , оси - вектором . Таблица вида
![]() ,
,
представляет собой геометрическую сумму указанных векторов, что определяет полное перемещение . Через единичные вектора можно записать сумму
![]() .
.
Направления, которые определяют площадки, где отсутствуют касательные напряжения, задаются единичными векторами , , . Тогда
![]() .
.
Если перемещения заданы в приращениях, то
![]() .
.
Через единичные вектора
![]() .
.
Перемещения, которые задаются единичными векторами , ,
![]() .
.
Проекции вектора определяют этот вектор и по модулю и по направлению. Действительно,
![]() ;
;![]()
![]()
![]() ,
,
где - углы между вектором и осями 1,2,3. При известных направляющих косинусах, известно направление вектора в пространстве. Это относится и к произвольным координатам . Направления 1,2,3 называют главными направлениями.
4.2. Деформации в элементарном объеме
Деформация любого элементарного объема тела (параллелепипед), может быть представлена из ряда отдельных простейших деформаций, т.е. разложена на составляющие. Имеется шесть составляющих деформаций: три линейных (удлинений) и три угловых (сдвиги). Линейные деформации обозначаются с индексом, указывающим направление удлинения. Положительной деформацией считается деформация удлинения. При данных деформациях изменяется объем и форма.
Положительному
сдвигу соответствует уменьшение угла
между направлением осей. Углы сдвига
(относительные сдвиги), проектирующиеся
на плоскость
![]() ,
обозначаются
,
обозначаются
![]() или
или
![]() ,
рис.4.2. Для других плоскостей -
,
рис.4.2. Для других плоскостей -
![]() или
или
![]() и т. д. Считается, что при малых углах
сдвига, объем остается неизменным.
Угловые деформации не влияют на линейные.
и т. д. Считается, что при малых углах
сдвига, объем остается неизменным.
Угловые деформации не влияют на линейные.
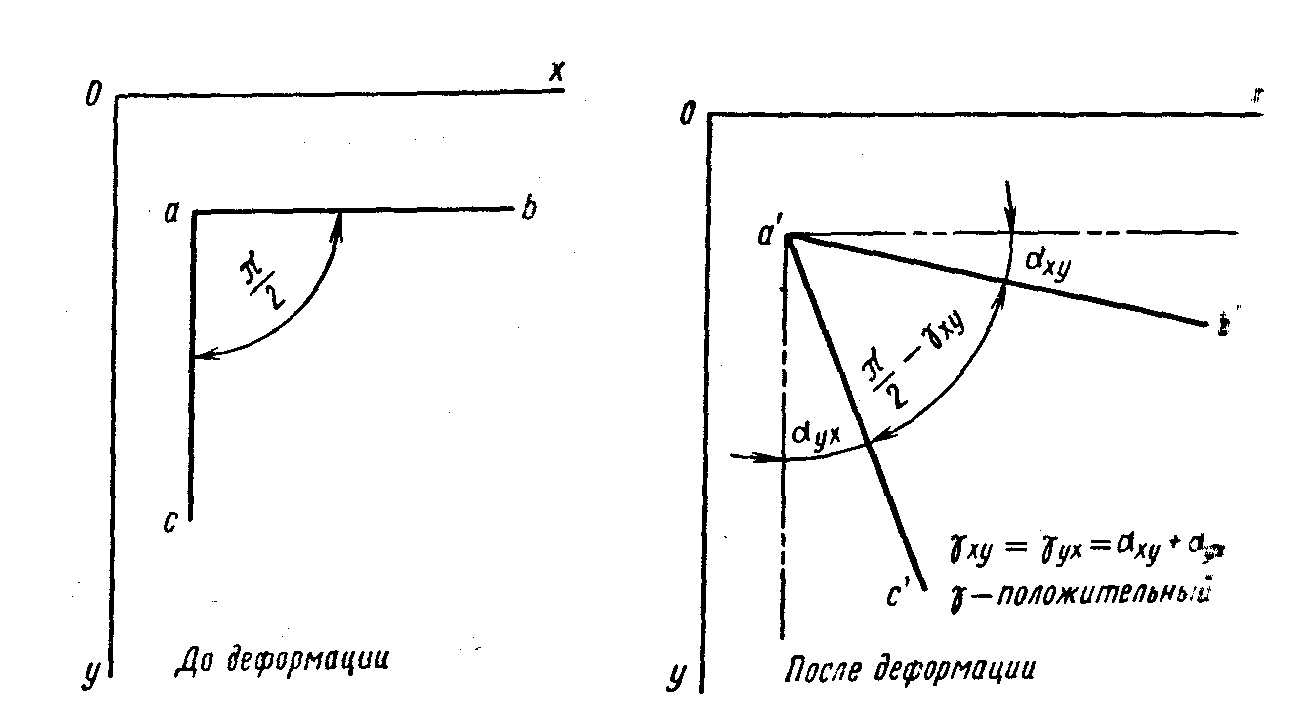
Рис.4.2. Угловые деформации
Выразим компоненты
деформаций через компоненты перемещений.
Выделим в точке тела элементарный объем
с бесконечно малыми ребрами
![]() ,
параллельными осям координат. Проекция
элементарного параллелепипеда на
плоскость
до
деформации, точка
является проекцией рассматриваемой
точки
,
параллельными осям координат. Проекция
элементарного параллелепипеда на
плоскость
до
деформации, точка
является проекцией рассматриваемой
точки
![]() на
плоскость, рис.4.3.
на
плоскость, рис.4.3.
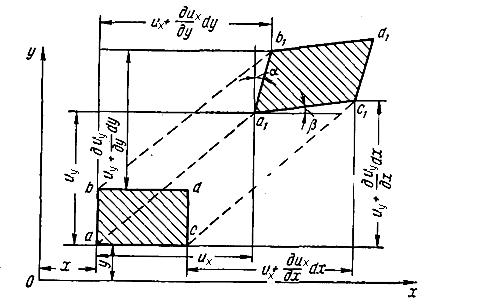
Рис.4.3. Перемещения точки в плоскости
После деформации
точки получили перемещения, и перешли
в положение со штрихом. В общем, все
перемещения зависят от координат, при
этом необходимо учитывать перемещения
связанные и с пластической деформацией.
Если перемещения вдоль соответствующих
осей зависят и от производных по этим
же координатам, то пластическое течение
совпадает с общим перемещением точки.
Если нет, то пластическое течение
перпендикулярно общему перемещению и
тогда появляются сдвиги. В первом случае
![]() ,
где
,
где
![]() - удлинение ребра в результате его
деформации вдоль оси
.
- удлинение ребра в результате его
деформации вдоль оси
.
Относительная
деформация
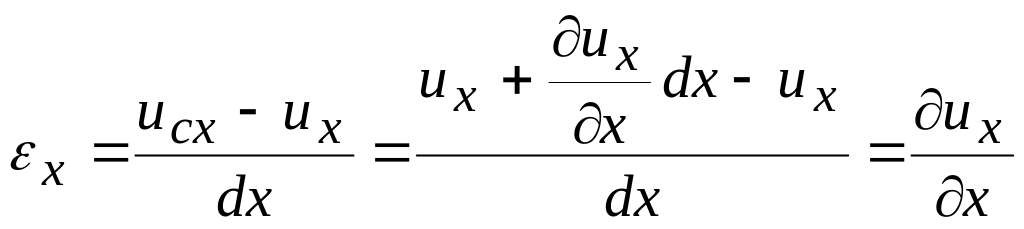 .
.
Аналогично получим
![]() ,
,
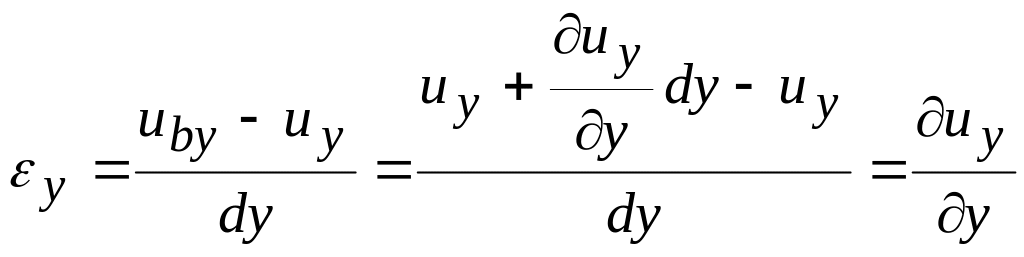 .
.
Во втором случае
![]() ;
;
![]() ,
где
,
где
![]() и
и
![]() - пластическое смещение векторов
перемещений
- пластическое смещение векторов
перемещений
![]() и
и
![]() в поперечном направлении
в поперечном направлении
![]() ,
что приводит к угловым сдвигам
,
что приводит к угловым сдвигам
![]() и
и
![]() .
Если их нет, смещаемые точки располагаются
на прямых параллельных осям координат.
Частные производные становятся равными
нулю. Принимая
.
Если их нет, смещаемые точки располагаются
на прямых параллельных осям координат.
Частные производные становятся равными
нулю. Принимая
![]() и
и
![]() ,
запишем
,
запишем
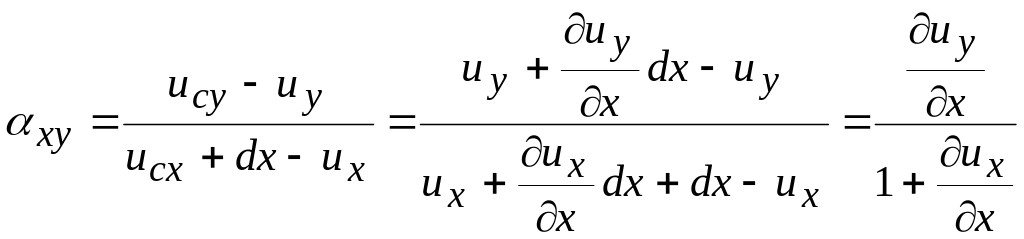 .
.
Так как
![]() значительно меньше единицы, то
значительно меньше единицы, то
![]() .
Тем же способом получим
.
Тем же способом получим
![]() .
Тогда
.
Тогда
![]() .
Следовательно
.
Следовательно
![]() .
Принято выражать сдвиги в виде
половинок, тогда
.
Принято выражать сдвиги в виде
половинок, тогда
![]() ,
,
![]() .
Причем
.
Причем
![]() .
Индексация будет совпадать с индексацией
касательных напряжений и касательных
перемещений в предыдущем разделе. В
итоге получим: относительные удлинения
.
Индексация будет совпадать с индексацией
касательных напряжений и касательных
перемещений в предыдущем разделе. В
итоге получим: относительные удлинения
![]() ,
,
![]() ,
,
![]() ,
относительные
сдвиги
,
относительные
сдвиги
,
![]() ,
,
![]() .
.
Эти уравнения получим О.Л.Коши. Линейные и сдвиговые деформации можно записать в виде таблицы
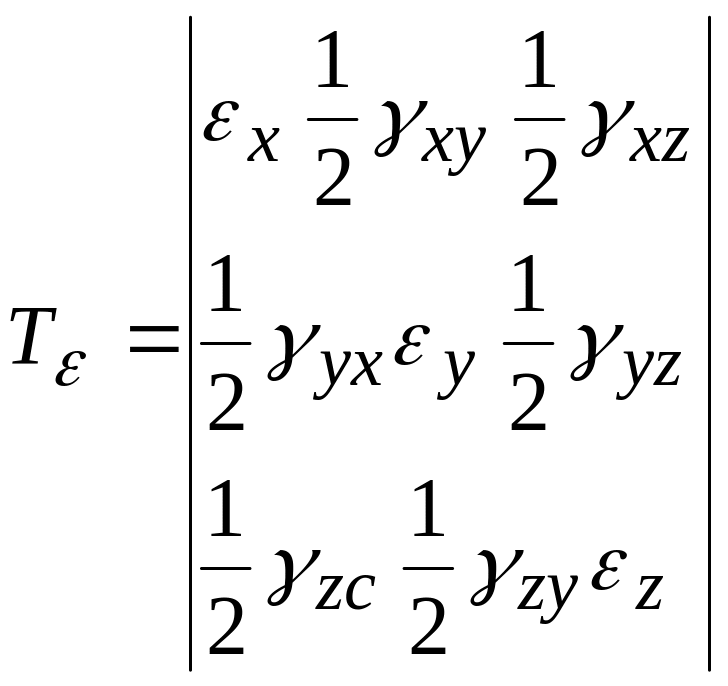 .
.
Значение
![]() является тензором деформаций, обладающий
такими же свойствами, как и тензор
напряжений. Он полностью определяет
деформированное состояние точки.
является тензором деформаций, обладающий
такими же свойствами, как и тензор
напряжений. Он полностью определяет
деформированное состояние точки.
Из последних соотношений определим элементарные перемещения точек в результате пластической деформации, тогда
![]() ,
,
![]()
![]() .
.
Если подставить
последние соотношения в выражение для
определения приращения вектора
перемещения с учетом, что
![]() ,
тогда
,
тогда
![]() ,
,
или
![]() .
.
Для осесимметричного напряженного состояния в цилиндрических координатах без вывода:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Следует подчеркнуть,
что пластической деформации в направлении
координаты
нет. Деформация
![]() определяется геометрическими построениями.
определяется геометрическими построениями.
Можно показать, что в цилиндрических координатах при объемном напряженно-деформированном состоянии компоненты тензора деформаций имеют вид
,
![]() ,
,
,
,
![]() ,
,
![]() .
.
На границе перемещение можно представить в виде
![]() ,
,
не раскладывая предварительно на составляющие по главным направлениям.
