
- •1. Випадкові події, їх класифікація, приклади. Класичне правило обчислення ймовірностей
- •2. Множення.
- •8. Ймовірність появи однієї з двох сумісних подій. Узагальнення теореми
- •9. Незалежні події. Ймовірність добутку двох незалежних подій. Узагальнення теореми
- •10. Залежні події. Умовна ймовірність. Ймовірність добутку двох подій. Узагальнення теореми
- •11.Теорема про повну ймовірність
- •12. Формули Байєса
- •15. Інтегральна теорема Муавра-Лапласса. Інтегральна функція Лапласса, властивості функції.
- •16.Теорема Пуассона. Поняття найвірогіднішого числа, властивості
- •17. Означення випадкових величин, дискретні і неперервні випадкові величини. Закон розподілу вв та многокутник розподілу.
- •18.Функція розподілу. Означення, властивості, графік.
- •19.Щільність ймовірностей. Властивості, графік
- •20. Залежні і незалежні випадкові величини. Операції над випадковими величинами
- •21. Математичне сподівання двв. Властивості математичного сподівання
- •22.Дисперсія двв і її властивості. Середнє квадратичне відхилення
- •23. Початкові і центральні моменти двв. Мода, медіана, асиметрія, ексцес.
- •24.Неперервні випадкові величини. Числові характеристики нвв.
- •25.Означення багатовимірної випадкової величини. Двовимірна випадкова величина. Закон розподілу двовимірної випадкової величини. Умовний розподіл
- •26.Функція розподілу п-вимірної випадкової величини. Функція розподілу двовимірної в.В. Властивості функції розподілу.
- •27.Коваріація та її властивості. Коефіцієнт кореляції. Властивості коефіцієнта кореляції
- •28.Біномний закон розподілу. Числові характеристики
- •29. Закон розподілу Пуассона, числові характеристики, використання
- •30. Геометричний розподіл, числові характеристики, використання
- •31. Гіпергеометричний закон розподілу, числові характеристики.
- •33. Інтегральна фунція розподілу та щільність ймовірностей показникового розподілу, графіки, числові характеристики.
- •34. Нормально розподілена випадкова величина. Графік щільності нормального розподілу, властивості функції. Правило трьох сигм.
- •35. Розподіли: хі-квадрат, Стьюдента та логнормальний. Числові характеристики
- •37. Предмет, методи і завдання математичної статистики. Об`єм сукупності
- •38. Генеральна та вибіркові сукупності. Статистичний розподіл вибірки
- •39. Полігон частот і відносних частот
- •40. Гістограма частот і відносних частот
- •41. Емпірична функція розподілу f*(X) та її властивості
- •42. Вибіркова середня та її властивості. Степеневі середні вибірки
- •44. Мода і медіана статистичного розподілу вибірки, коефіцієнт варіацій, варіаційний розмах.
- •47. Означення довірчого інтервалу. Довірчий інтервал для оцінки математичного сподівання нормального розподілу
- •48. Статистичні гіпотези та їх різновиди. Помилки першого та другого роду
- •49. Статистичний критерій. Потужність критерію. Рівень значущості критерію
- •50. Критична область. Області прийняття гіпотез. Алгоритм перевірки статистичної гіпотези
- •51. Критерій узгодження Пірсона. Алгоритм використання критерію Пірсона
- •52. Критерій узгодження Колмогорова
- •53. Метод моментів та метод максимальної правдоподібності знаходження точкових оцінок
- •54. Метод найменших квадратів при знаходженні точкових оцінок
- •55. Поняття про функціональну, статистичну і кореляційну залежності.
- •56. Рівняння лінійної регресії. Довірчий інтеграл для лінії регресії
44. Мода і медіана статистичного розподілу вибірки, коефіцієнт варіацій, варіаційний розмах.
мода (Mo). Модою дискретного статистичного розподілу вибірки називають варіанту, що має найбільшу частоту появи.
Мод може бути кілька. Коли дискретний статистичний розподіл має одну моду, то він називається одномодальним, коли має дві моди — двомодальним і т. д.;
медіана (Me). Медіаною дискретного статистичного розподілу вибірки називають варіанту, яка поділяє варіаційний ряд на дві частини, рівні за кількістю варіант; Коефіцієнт варіації) — відносна величина, що служить для характеристики коливання (мінливості) ознаки. Являє собою відношення середнього квадратичного відхилення τ до середнього арифметичного Х, виражається у відсотках: ν = τ/Х[1].Коефіцієнт варіації застосовується тоді, коли необхідно оцінити мінливість ознак об'єкта, які виражені в різних одиницях вимірювання[2].Варіювання вважається слабким, якщо ν<10%, якщо ν від 11-25%, то середнім і значним при ν>25%.
Варіаційний розмах R — це різниця між максимальним і мінімальним значеннями ознаки: R = xmax – xmin. Він характеризує діапазон варіації, його розсіювання
45.Початкові та центральні емпіричні моменти. Асиметрія і ексцес статистичного розподілу вибірки.
Вибірковим початковим емпіричним моментом порядку S статистичного розподілу вибірки називається середнє арифметичне значення степенів порядку S варіант xi.
 ,
,
 ,
S=3….S
,
S=3….S
Вибірковим центральним емпіричним моментом порядку S статистичного розподілу вибірки називається середнє арифметичне значення степенів порядку S відхилень його варіант від середнього вибіркового значення
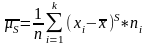
Центральний емпіричний момент 1-го порядку дорівнює 0, другого – S^2
Коефіцієнтом асиметрії варіаційного ряду називається число, яке дорівнює відношенню центрального емпіричного моменту 3-го порядку до куба середнього квадратичного відхилення. Якщо А=0, то розподіл варіант має симетричну форму
 .
Якшо асиметрія А>0 (A<0), то говорять
про додатню правосторонню (від`ємну
лівосторонню) асиметрію.
.
Якшо асиметрія А>0 (A<0), то говорять
про додатню правосторонню (від`ємну
лівосторонню) асиметрію.
Ексцесом
варіаційного ряду називається число,
яке дорівнює різниці між відношенням
центрального емпіричного моменту 4-го
порядку до середнього квадратичного
4-го степеня і віднявши 3.

Ексцес є показником крутості варіаційного ряду в порівнянні із звичайним розподілом. Якщо Е>0, то полігон варіаційного ряду має більш круту вершину в порівнянні з нормальним розподілом, якщо E<0, то вершина є більш пологою.
46. Статистичні оцінки та вимоги до них. Точкові та інтервальні оцінки параметрів розподілу генеральної сукупності. Надійність оцінки.
Статистичні
оцінки, яку дістали на основі обробки
вибірки про ознаку генеральної сукупності,
завжди міститиме певні похибки, оскільки
вибірка становить лише незначну частину
від неї (n < N), тобто обсяг вибірки
значно менший від обсягу генеральної
сукупності.Тому слід організувати
вибірку так, щоб ця інформація була
найбільш повною (вибірка має бути
репрезентативною) і забезпечувала з
найбільшим ступенем довіри про параметри
генеральної сукупності або закон
розподілу її ознаки. Параметри
генеральної сукупності M(xi)=Xг,
Dг,
δг,
Mo, rxy
є величинами сталими, але їх числове
значення невідоме. Ці параметри оцінюються
параметрами вибірки:

 які дістають при обробці вибірки. Вони
є величинами непередбачуваними,
тобто випадковими.
які дістають при обробці вибірки. Вони
є величинами непередбачуваними,
тобто випадковими.
Тут
через θ позначено оцінювальний параметр
генеральної сукупності, а через
 — його статистичну оцінку, яку називають
ще статистикою. При цьому θ = const,
а
— випадкова величина, що має певний
закон розподілу ймовірностей. Зауважимо,
що до реалізації вибірки кожну її
варіанту розглядають як випадкову
величину, що має закон розподілу
ймовірностей ознаки генеральної
сукупності з відповідними числовими
характеристиками:M(xi)=Xг=M(x),
D(xi)=Dг,
δ(xi)=δг
— його статистичну оцінку, яку називають
ще статистикою. При цьому θ = const,
а
— випадкова величина, що має певний
закон розподілу ймовірностей. Зауважимо,
що до реалізації вибірки кожну її
варіанту розглядають як випадкову
величину, що має закон розподілу
ймовірностей ознаки генеральної
сукупності з відповідними числовими
характеристиками:M(xi)=Xг=M(x),
D(xi)=Dг,
δ(xi)=δг
Статистична
оцінка
 яка визначається одним числом, точкою,
називається точковою. Беручи до уваги,
що
є випадковою величиною, точкова
статистична оцінка може бути зміщеною
і незміщеною: коли математичне сподівання
цієї оцінки точно дорівнює оцінювальному
параметру θ, а саме:
яка визначається одним числом, точкою,
називається точковою. Беручи до уваги,
що
є випадковою величиною, точкова
статистична оцінка може бути зміщеною
і незміщеною: коли математичне сподівання
цієї оцінки точно дорівнює оцінювальному
параметру θ, а саме:
 (1)
то
називається незміщеною; в противному
разі, тобто коли
(1)
то
називається незміщеною; в противному
разі, тобто коли
 точкова статистична оцінка
називається зміщеною відносно параметра
генеральної сукупності θ. Різниця
точкова статистична оцінка
називається зміщеною відносно параметра
генеральної сукупності θ. Різниця (3) називається
зміщенням статистичної
оцінки
(3) називається
зміщенням статистичної
оцінки
 Оцінювальний
параметр може мати кілька точкових
незміщених статистичних оцінок Точкова
статистична оцінка називається
ефективною, коли при заданому обсязі
вибірки вона має мінімальну дисперсію.
Отже, оцінка
Оцінювальний
параметр може мати кілька точкових
незміщених статистичних оцінок Точкова
статистична оцінка називається
ефективною, коли при заданому обсязі
вибірки вона має мінімальну дисперсію.
Отже, оцінка
 буде незміщеною й ефективною.
буде незміщеною й ефективною.
Точкова
статистична оцінка називається
ґрунтовною, якщо у разі необмеженого
збільшення обсягу вибірки
наближається до оцінювального параметра
θ, а саме:
 Точкові статистичні оцінки
є випадковими величинами, а тому наближена
заміна θ на
часто призводить до істотних похибок,
особливо коли обсяг вибірки малий. У
цьому разі застосовують інтервальні
статистичні оцінки. Статистична оцінка,
що визначається двома числами, кінцями
інтервалів, називається інтервальною.
Різниця між статистичною оцінкою
та її оцінювальним параметром θ, взята
за абсолютним значенням, називається
точністю оцінки, а саме:
Точкові статистичні оцінки
є випадковими величинами, а тому наближена
заміна θ на
часто призводить до істотних похибок,
особливо коли обсяг вибірки малий. У
цьому разі застосовують інтервальні
статистичні оцінки. Статистична оцінка,
що визначається двома числами, кінцями
інтервалів, називається інтервальною.
Різниця між статистичною оцінкою
та її оцінювальним параметром θ, взята
за абсолютним значенням, називається
точністю оцінки, а саме:
 (04)
де δ є точністю оцінки. Оскільки
є випадковою величиною, то і δ буде
випадковою, тому нерівність (04)
справджуватиметься з певною ймовірністю.
Імовірність, з якою береться нерівність
(04), тобто
(04)
де δ є точністю оцінки. Оскільки
є випадковою величиною, то і δ буде
випадковою, тому нерівність (04)
справджуватиметься з певною ймовірністю.
Імовірність, з якою береться нерівність
(04), тобто
 ,
(05) називають надійністю. Рівність (05)
можна записати так:
,
(05) називають надійністю. Рівність (05)
можна записати так:
 .
Інтервал
.
Інтервал
 ,
,
що покриває оцінюваний параметр θ генеральної сукупності з заданою надійністю , називають довірчим
Надійністю
(або надійною ймовірністю) оцінки
 за
називається ймовірність
за
називається ймовірність
 ,
,
з якою
здійснюється нерівність (1):
 .
.
Замінивши нерівність (1) тотожною подвійною нерівністю


 ,
отримаємо
,
отримаємо
 ,
(3)
,
(3)
Тобто
ймовірність того, що інтервал
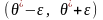 (4)
(4)
заключає в собі невідомий параметр , дорівнює .
Такий інтервал називають надійним інтервалом (інтервалом довіри).
На
практиці надійність оцінки звичайно
задається наперед. Найчастіше задають



