16.Теорема Пуассона. Поняття найвірогіднішого числа, властивості

17. Означення випадкових величин, дискретні і неперервні випадкові величини. Закон розподілу вв та многокутник розподілу.

Випадковою називається величина, яка може набувати різних числових значень. Строгіше означення випадкової величини пов’язане з поняттям простору елементарних подій. Нехай задано простір елементарних подій . Однозначна числова функція яку задано на просторі елементарних подій, називається випадковою величиною.

Якщо простір  дискретний, то випадкова величина дискретна. Неперервному простору елементарних подій відповідає неперервна випадкова величина.

Співвідношення між значеннями випадкової величини і їхніми ймовірностями називається законом розподілу випадкової величини.

Для дискретних випадкових величин закони розподілу можуть задаватися множиною значень, що їх набуває випадкова величина, і ймовірностями цих значень.

Якщ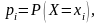о то або, якщо величина набуває зліченної множини значень, то Закони розподілу дискретних випадкових величин задаються у табличній формі (подаються значення випадкової величини і їхні ймовірності), аналітичній (наводиться формула, за якою обчислюються ймовірності для заданих значень випадкової величини), графічній (у прямокутній системі координат задається набір точок сполучивши точки відрізками прямих, дістане­мо многокутник розподілу ймовірностей).

18.Функція розподілу. Означення, властивості, графік.

Універсальним способом задання закону розподілу ймовірностей є функція розподілу Цю функцію можна тлумачити так:унаслідок експерименту випадкова величина може набути значення, меншого за х. Для дискретних величин

Функція розподілу — неспадна, неперервна зліва,

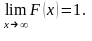
Для довільних

Якщо Х — неперервна випадкова величина, то — неперервна і диференційована; її похідна називається щільністю розподілу ймовірностей. При цьому — невід’ємна функція, для якої

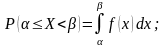
Властивості:

1.0F(x)1

2.F(x) є неспадною функцією,а саме F(x₂)F(x₁), якщо х₂х₁

Графік функції розподілу може мати такий вигляд:_S-

19.Щільність ймовірностей. Властивості, графік

Диференціальною функцією розподілу або щільністю імовірностей НВВ називають похідну І-го порядку від її інтегральної функції розподілу

Диференціальна функція розподілу має такі властивості:

f(x)=>0, тому що вона є похідною зростаючої функції F(x)

f(x)=0 при x<a та x=>b, тому що є похідною F(x)=0 при x<a та F(x)=1 при x=>b

S+&-&f(x)dx=1, тому що подія {-&<X<+&} – достовірна.

Графік щільності імовірностей f(x) називають кривою розподілу.

20. Залежні і незалежні випадкові величини. Операції над випадковими величинами

Поняття залежності (незалежності) - одне з найважливіших понять теорії ймовірностей.

Випадкова величина називається незалежною від випадкової величини , якщо закон розподілу не залежить від того, яке значення прийняла випадкова величина :

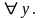= , (24)

Аналогічно для випадкової величини : = ,

Якщо випадкова величина залежить від , то (25)

і аналогічно .

Для дискретних випадкових величин незалежність означає виконання умов

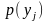= , = (26)

Якщо умови (26) не виконуються хоч би для однієї пари значень , то це означає залежність випадкових величин.

Над випадковими величинами можна проводити такі ж самі операції, як і над випадковими подіями.

Об'єднанням випадкових величин Х і Y називаємо випадкову величину, можливі значення якої дорівнюють сумам всіх мо­жливих доданків, а ймовірності випадкової величини для незалежних величин і – добутку ймовірностей, для залежних величин – добуткам ймовірностей однієї з них на умовну ймовірність другої.

Перетином незалежних випадкових величин X і Y називають випадкову величину, можливі значення якої дорівнюють добуткам всіх можливих значень і –, ймовірності яких також перемножуються