
- •1. Випадкові події, їх класифікація, приклади. Класичне правило обчислення ймовірностей
- •2. Множення.
- •8. Ймовірність появи однієї з двох сумісних подій. Узагальнення теореми
- •9. Незалежні події. Ймовірність добутку двох незалежних подій. Узагальнення теореми
- •10. Залежні події. Умовна ймовірність. Ймовірність добутку двох подій. Узагальнення теореми
- •11.Теорема про повну ймовірність
- •12. Формули Байєса
- •15. Інтегральна теорема Муавра-Лапласса. Інтегральна функція Лапласса, властивості функції.
- •16.Теорема Пуассона. Поняття найвірогіднішого числа, властивості
- •17. Означення випадкових величин, дискретні і неперервні випадкові величини. Закон розподілу вв та многокутник розподілу.
- •18.Функція розподілу. Означення, властивості, графік.
- •19.Щільність ймовірностей. Властивості, графік
- •20. Залежні і незалежні випадкові величини. Операції над випадковими величинами
- •21. Математичне сподівання двв. Властивості математичного сподівання
- •22.Дисперсія двв і її властивості. Середнє квадратичне відхилення
- •23. Початкові і центральні моменти двв. Мода, медіана, асиметрія, ексцес.
- •24.Неперервні випадкові величини. Числові характеристики нвв.
- •25.Означення багатовимірної випадкової величини. Двовимірна випадкова величина. Закон розподілу двовимірної випадкової величини. Умовний розподіл
- •26.Функція розподілу п-вимірної випадкової величини. Функція розподілу двовимірної в.В. Властивості функції розподілу.
- •27.Коваріація та її властивості. Коефіцієнт кореляції. Властивості коефіцієнта кореляції
- •28.Біномний закон розподілу. Числові характеристики
- •29. Закон розподілу Пуассона, числові характеристики, використання
- •30. Геометричний розподіл, числові характеристики, використання
- •31. Гіпергеометричний закон розподілу, числові характеристики.
- •33. Інтегральна фунція розподілу та щільність ймовірностей показникового розподілу, графіки, числові характеристики.
- •34. Нормально розподілена випадкова величина. Графік щільності нормального розподілу, властивості функції. Правило трьох сигм.
- •35. Розподіли: хі-квадрат, Стьюдента та логнормальний. Числові характеристики
- •37. Предмет, методи і завдання математичної статистики. Об`єм сукупності
- •38. Генеральна та вибіркові сукупності. Статистичний розподіл вибірки
- •39. Полігон частот і відносних частот
- •40. Гістограма частот і відносних частот
- •41. Емпірична функція розподілу f*(X) та її властивості
- •42. Вибіркова середня та її властивості. Степеневі середні вибірки
- •44. Мода і медіана статистичного розподілу вибірки, коефіцієнт варіацій, варіаційний розмах.
- •47. Означення довірчого інтервалу. Довірчий інтервал для оцінки математичного сподівання нормального розподілу
- •48. Статистичні гіпотези та їх різновиди. Помилки першого та другого роду
- •49. Статистичний критерій. Потужність критерію. Рівень значущості критерію
- •50. Критична область. Області прийняття гіпотез. Алгоритм перевірки статистичної гіпотези
- •51. Критерій узгодження Пірсона. Алгоритм використання критерію Пірсона
- •52. Критерій узгодження Колмогорова
- •53. Метод моментів та метод максимальної правдоподібності знаходження точкових оцінок
- •54. Метод найменших квадратів при знаходженні точкових оцінок
- •55. Поняття про функціональну, статистичну і кореляційну залежності.
- •56. Рівняння лінійної регресії. Довірчий інтеграл для лінії регресії
47. Означення довірчого інтервалу. Довірчий інтервал для оцінки математичного сподівання нормального розподілу
Інтервал , що покриває оцінюваний параметр θ генеральної сукупності з заданою надійністю , називають довірчим. Кінці довірчого інтервалу є випадковими величинами
Надійні інтервали для оцінки математичного сподівання
нормального
розподілу при відомому
 .
.
Нехай
відомо, що випадкова величина Х розподілена
нормально і
- її середнє квадратичне відхилення.
Потрібно побудувати інтервальну оцінку
для невідомого математичного сподівання
 .
Точковою оцінкою для математичного
сподівання є вибіркове середнє
.
Точковою оцінкою для математичного
сподівання є вибіркове середнє
 .
(5)
.
(5)
Середнє
вибіркове
 є різним для окремо взятих вибірок з
генеральної сукупності, отже його можна
розглядати як випадкову величину
є різним для окремо взятих вибірок з
генеральної сукупності, отже його можна
розглядати як випадкову величину
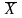 ,
а значення
,
а значення
 як однаково розподілені незалежні
випадкові величини
(
як однаково розподілені незалежні
випадкові величини
( ).
Оскільки значення
незалежні, то
).
Оскільки значення
незалежні, то
 ,
,
 ,
,
Вважаємо,
що
 - відома величина.
- відома величина.
Нерівність
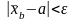 (6)
(6)
повинна
виконуватись із заданою ймовірністю
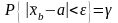
або, замінивши нерівність (6) еквівалентною нерівністю, отримаємо
 ,
(7)
,
(7)
Пригадаємо,
що для нормально розподіленої випадкової
величини Х з параметрами а і
ймовірність попадання в інтервал
 визначається за формулою
визначається за формулою
де
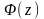 - функція Лапласа (табульована).
- функція Лапласа (табульована).
Тоді
співвідношення (7) можна переписати так
 .
.
Позначивши
 ,
маємо рівняння
,
маємо рівняння
 ;
(8)
;
(8)
Таким
чином, остаточно отримаємо 
Тобто
побудований надійний інтервал
 (9)
(9)
заключає
в собі невідомий параметр а (математичне
сподівання) з ймовірністю
.
Число
 при заданому значенні
знаходимо із таблиці значень функції
Лапласа.
при заданому значенні
знаходимо із таблиці значень функції
Лапласа.
Висновки:
1) при
збільшенні обсягу
вибірки число
 зменшується, тобто точність оцінки
зменшується, тобто точність оцінки
збільшується;
2)
зростання надійності
 веде до збільшення
,
отже, до зростання
веде до збільшення
,
отже, до зростання
 ,
або до зменшення точності.
,
або до зменшення точності.
48. Статистичні гіпотези та їх різновиди. Помилки першого та другого роду
Статистичними називають гіпотези про вигляд розподілу генеральної сукупності або про параметри відомих розподілів.
Наприклад, статистичними будуть гіпотези: генеральна сукупність розподілена за нормальним законом; дисперсія двох сукупностей, розподілених за законом Пуассона, рівні між собою.
Гіпотезу,
що підлягає перевірці, називають
основною. Оскільки ця гіпотеза припускає
відсутність систематичних розбіжностей
(нульові розбіжності) між невідомим
параметром генеральної сукупності і
величиною, що одержана внаслідок обробки
вибірки, то її називають нульовою
гіпотезою і позначають Н0.
Зміст нульової гіпотези записується
так: ;
; ;
; .
Кожній нульовій гіпотезі можна
протиставити кілька альтернативних
(конкуруючих) гіпотез, які позначають
символом Н,
що заперечують твердження нульової.
Так, наприклад, нульова гіпотеза
стверджує:
.
Кожній нульовій гіпотезі можна
протиставити кілька альтернативних
(конкуруючих) гіпотез, які позначають
символом Н,
що заперечують твердження нульової.
Так, наприклад, нульова гіпотеза
стверджує:
 ,
а альтернативна гіпотеза —
,
а альтернативна гіпотеза —
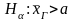 ,
тобто заперечує твердження нульової.
,
тобто заперечує твердження нульової.
Гіпотезу називають простою, якщо вона містить лише одне припущення, складною, якщо вона складається із скінченної чи нескінченної кількості простих гіпотез.
Якщо за висновком буде відкинута правильна гіпотеза, то кажуть, що це помилка першого роду. Якщо за висновком буде прийнята неправильна гіпотеза, то кажуть що це помилка другого роду.
