4.2 Критерий устойчивости Гурвица

где - характеристический полином разомкнутой системы

где - характеристический полином замкнутой системы.

Правило составления матрицы Гурвица

По главной диагонали вписываются коэффициенты в порядке убывания, начиная с и заканчивая . Справа главной диагонали записываются коэффициенты с возрастающими индексами, слева – с убывающими. если индекс больше n, либо меньше 0, то коэффициенты матрицы заменяются нулями.

Отчёркивая соответствующее количество строк или столбцов, вычислим определитель матрицы Гурвица.

Для устойчивости системы по Гурвицу необходимо и достаточно, чтобы при положительном коэффициенте все определители матрицы Гурвица были положительны .

Если , то система находится на границе устойчивости.

В силу специфики матрицы Гурвица (последняя строка) содержит один не нулевой элемент:

Из условия можно найти критический коэффициент усиления . Для устойчивости системы .

Покажем, что необходимым, но недостаточным условием устойчивости является положительность всех коэффициентов характеристического полинома.

1.

для характеристического полинома 1-ого порядка положительность коэффициентов является необходимым и достаточным условием устойчивости.

2.

3.

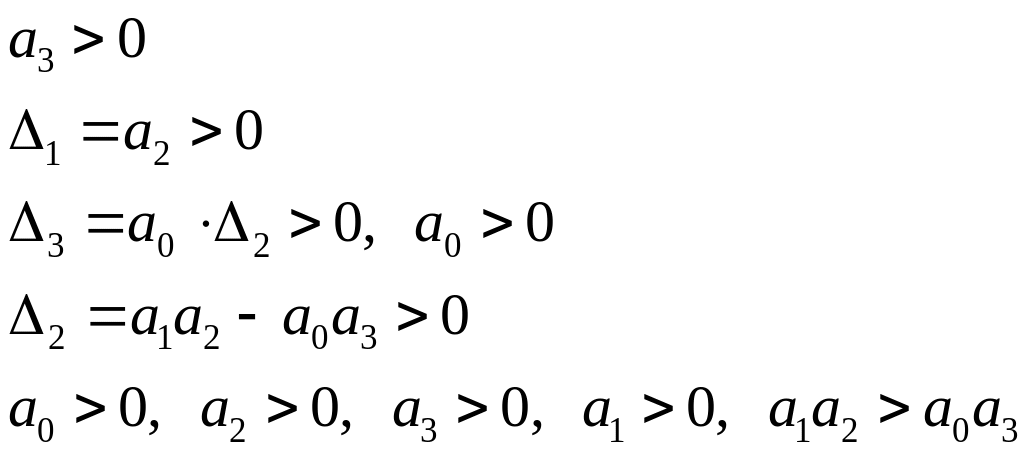
4.2.1 Методика определения устойчивости по критерию Гурвица

1. Найдём передаточную функцию разомкнутой цепи

.

2. Найдём передаточную функцию замкнутой цепи

.

3. Найдём характеристический полином

4. Составим матрицу Гурвица.

5. Убедиться, что при

4.2.2 Методика определения критического коэффициента усиления

Пункты 1 - 4 повторить

5. Найти критический коэффициент усиления из условия

4.3 Критерий Михайлова

В 1938г. Отечественный учёный А.В. Михайлов впервые предложил использовать частотные методы для анализа устойчивости систем.

Пусть задана замкнутая система, структурная схема которой имеет следующий вид:

,

где .

Решив это уравнение, найдём корни , тогда характеристический полином можно записать в виде:

.

Заменяя , получим характеристический полином Михайлова:

.

Каждый сомножитель представляет собой вектор, начало которого находится в точке корня , а конец - на мнимой оси.

.

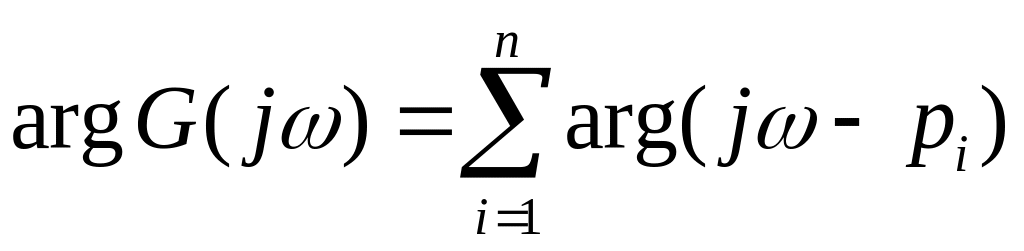Рассмотрим частные случаи:

1. Пусть все корни лежат в левой полуплоскости комплексной плоскости, то есть система устойчива.

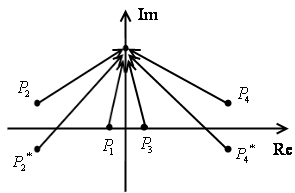
При изменении частоты от до каждый вектор повернётся на угол , тогда , .

2. Пусть корней находиться в правой полуплоскости, каждый из корней повернётся на угол , тогда ,

.

Первое определения устойчивости. Для устойчивости системы по Михайлову необходимо и достаточно, чтобы при изменении частоты от до приращение аргумента вектора было равно . Для неустойчивости системы приращение аргумента будет равно .

Рассмотрим другие формулировки критерия устойчивости по Михайлову. Для этого характеристический полином запишем в виде:

,

где

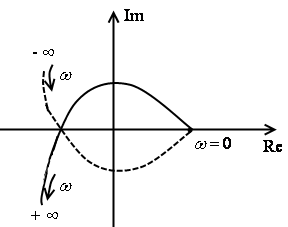
Анализ реальной и мнимой части характеристического полинома Михайлова показывает, что реальная часть является чётной функцией частоты, а мнимая – нечётной функцией. Из этого следует, что годограф Михайлова симметричен относительно реальной оси.

Второе определение устойчивости. Для устойчивости системы по Михайлову необходимо и достаточно, чтобы при изменении частоты от до , то приращение аргумента вектора было равно ,

Для неустойчивой системы , .

Примеры годографов устойчивых систем

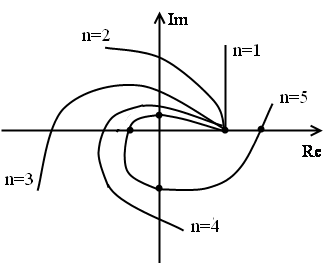
Пример годографа неустойчивой системы

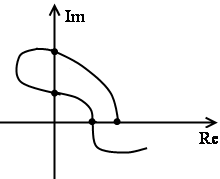
Третье определение устойчивости. Для устойчивости системы по Михайлову необходимо и достаточно, чтобы знаки значения годографа в точке пересечения с реальной осью чередовались, и знаки значения годографа в точках пересечения с минимальной осью так же чередовались.

Если годограф проходит через начало координат, то такая система находится на границе устойчивости.

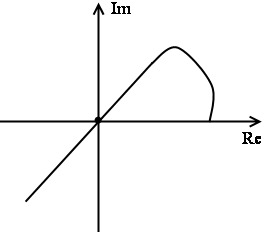
Критическим будем называть частоты, при которых годограф пересекает реальную ось.