9.4.2 Уравнение и передаточная функция разомкнутой импульсной системы

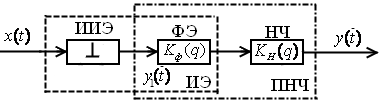
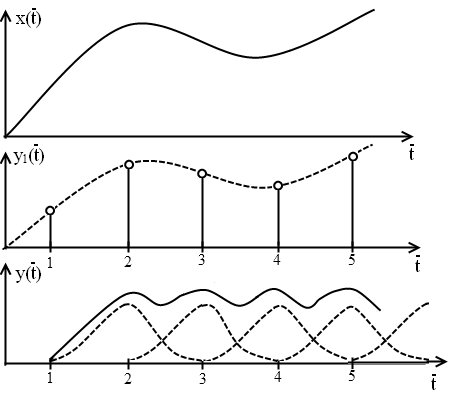
Из рисунка видно, что выходной сигнал будет равен .

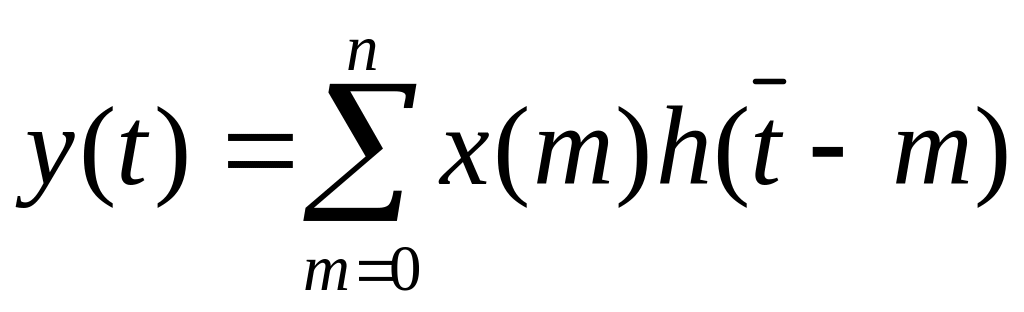Полагая, что , получим уравнение разомкнутой системы в области оригинала .

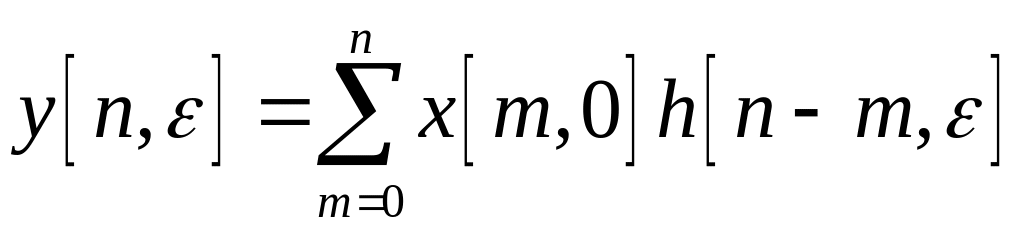Вычислив - преобразования левой и правой части, получим уравнение разомкнутой импульсной системы в области оригинала

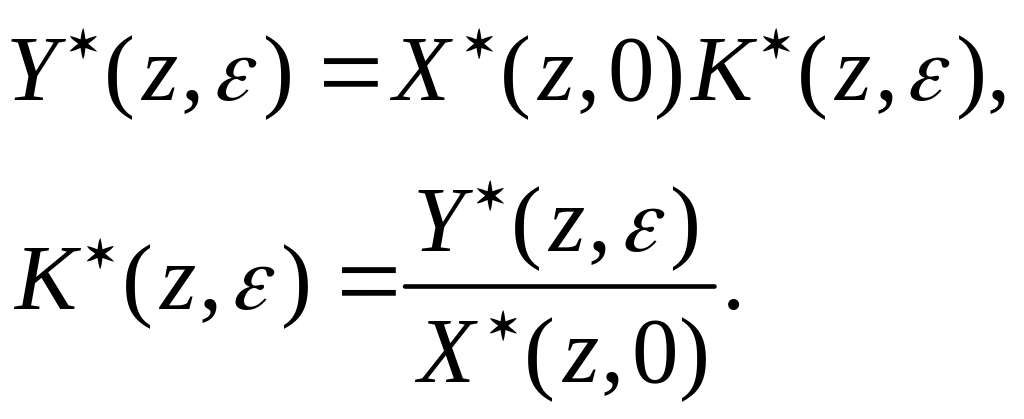
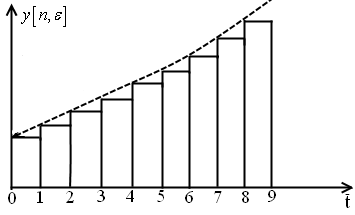
9.4.3 Переходные и установившиеся процессы разомкнутых импульсных систем

Решётчатую функцию выходного сигнала можно найти из обратного преобразования Лапласа .

Если , то решётчатая функция изображение её будет равно ,

.

9.4.4 Методика определения передаточной функции разомкнутой импульсной системы в области - преобразований

1. Определим передаточную функцию непрерывной части в области обычного преобразования Лапласа .

2. Найдём передаточную функцию непрерывной части в области безразмерного параметра

.

3. Найдём передаточную функцию ФЭ для обычного преобразования Лапласа

.

4. Найдём передаточную функцию ФЭ для безразмерного преобразования Лапласа

.

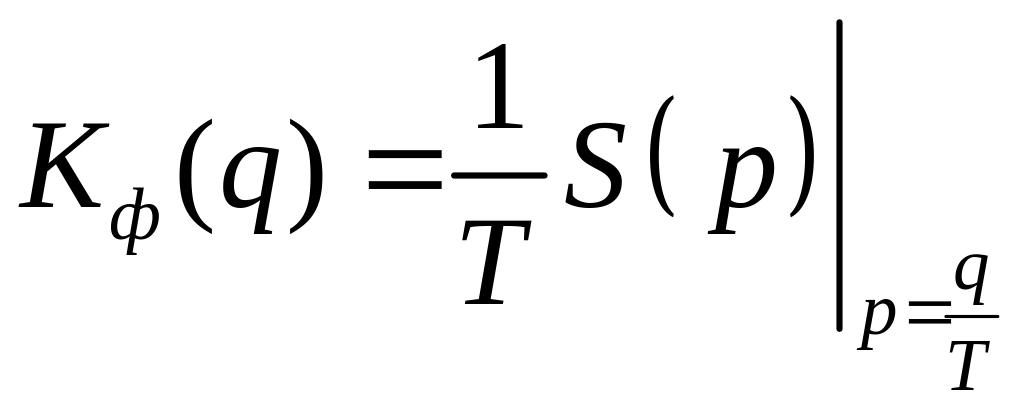5. Найдём передаточную функцию ПНЧ .

6. Определим импульсную характеристику для безразмерного времени .

7. Найдём решётчатую импульсную характеристику .

8. Найдём передаточную функцию в области - преобразований .

Пример №1. Определить выходной сигнал импульсной системы, ФЭ которой представляет безынерционный усилитель, а непрерывная часть является интегрирующим звеном .

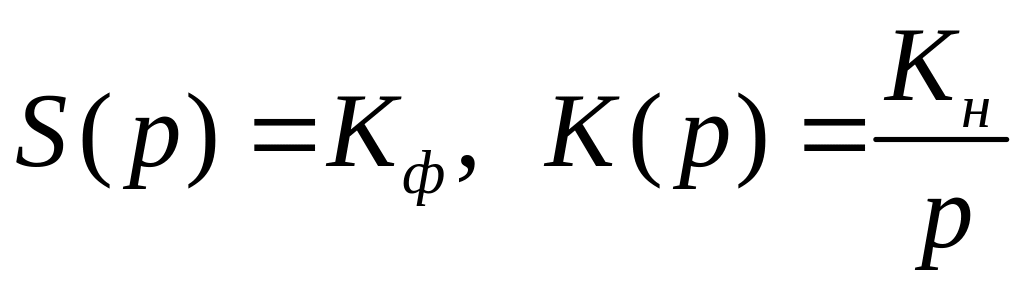1. Определить передаточную функцию разомкнутой импульсной системы

1.1 .

1.2 .

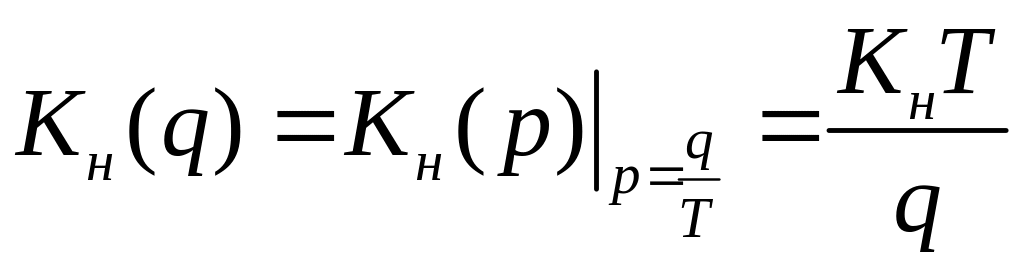1.3 .

1.4 .

1.5 .

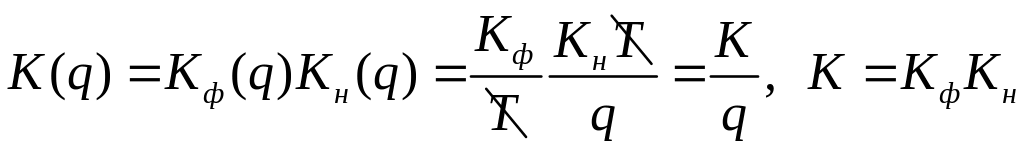1.6 .

1.7 .

1.8 .

2. Определим изображение входного воздействия

.

3. Найдём выходной сигнал ,

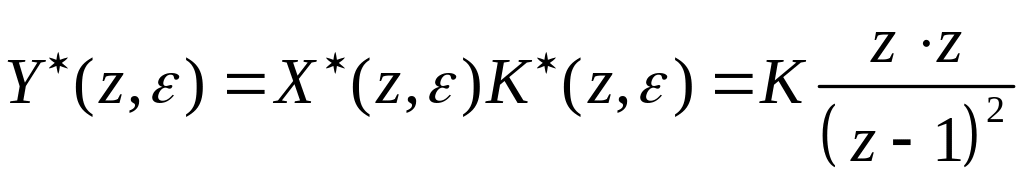, тогда .

Пример №2. Те же условия, но непрерывная часть являет собой инерционное звено.

1. Определить передаточную функцию разомкнутой импульсной системы

1.1 .

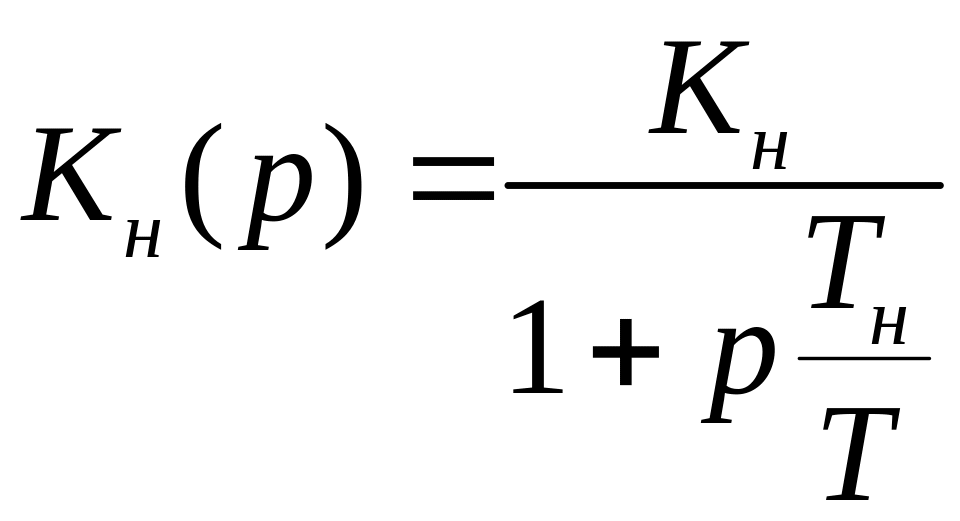1.2 .

1.3 .

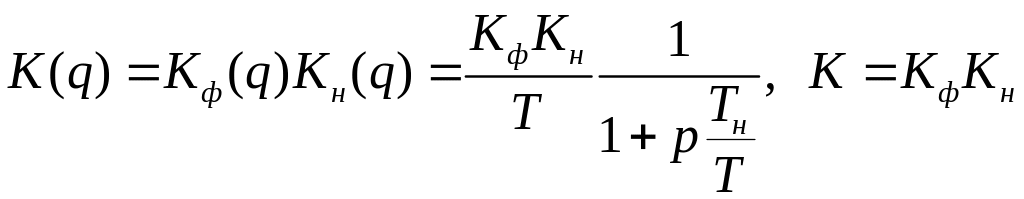1.4 .

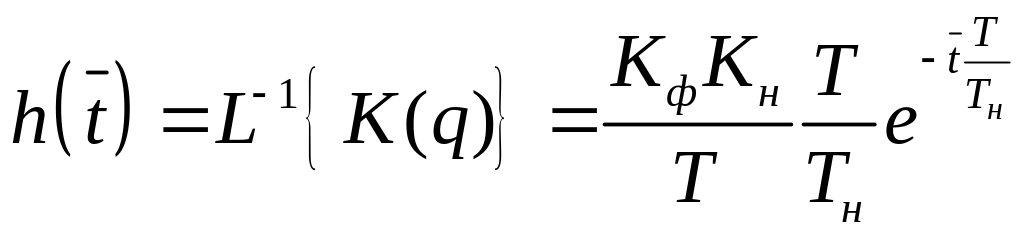1.4 .

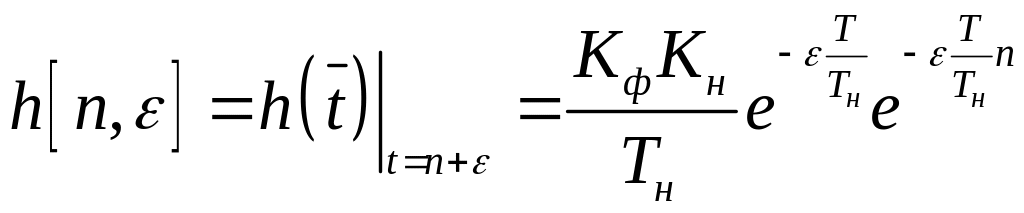1.6 .

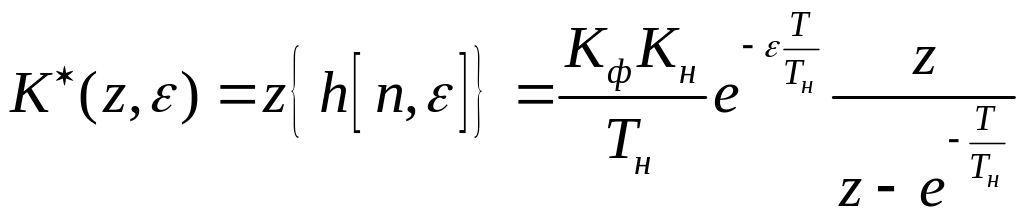2. Найдём выходной сигнал ,

.

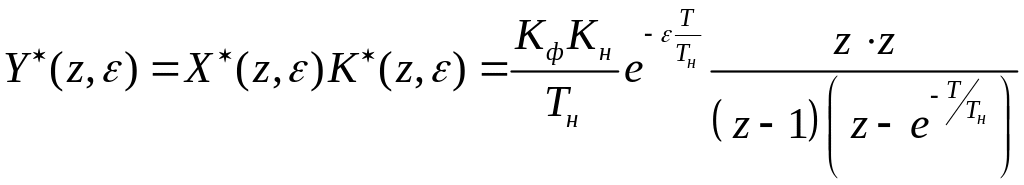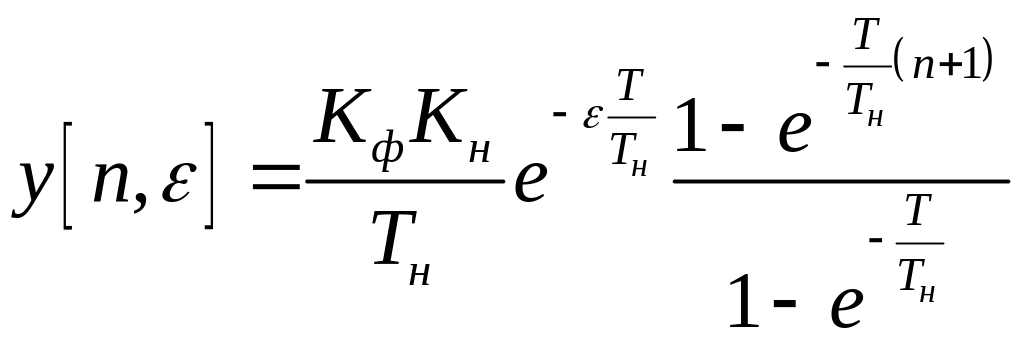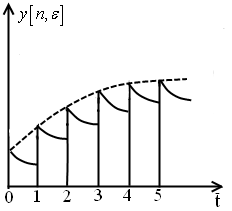
9.5 Анализ замкнутых систем прерывистого регулирования

9.5.1 Передаточная функция замкнутой системы прерывистого регулирования

Структурная схема системы прерывистого регулирования имеет следующий вид:

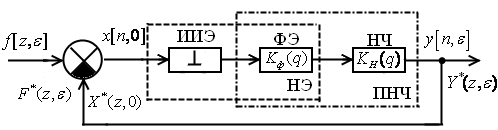
Система ничем не отличается от разомкнутой, только ввели обратную связь. Из рисунка видно, что

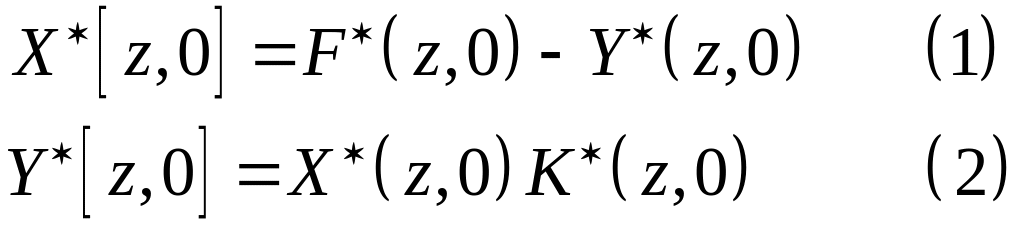
где - передаточная функция разомкнутой системы.

Подставляя (2) в (1) и решая уравнение относительно , получим:

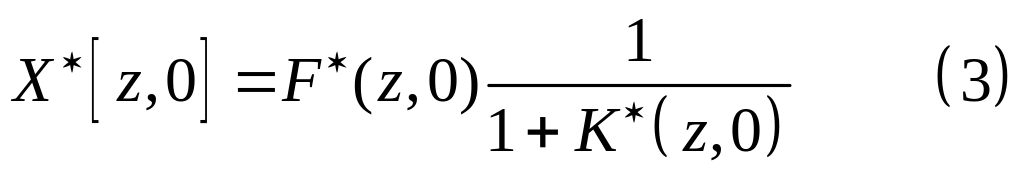, отсюда передаточная функция по ошибке

.

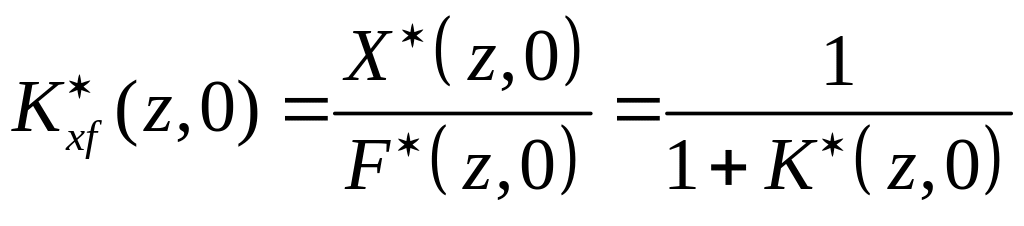Подставляя (3) в (2), получим выражение для передаточной функции замкнутой системы:

,

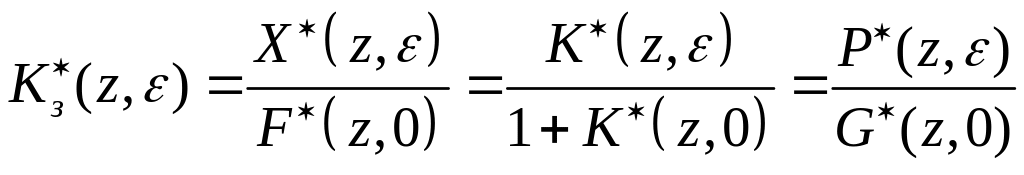где - характеристический полином замкнутой системы.

9.5.2 Установившейся и переходный режимы в замкнутых системах прерывистого регулирования

Изображение выходного сигнала имеет вид:

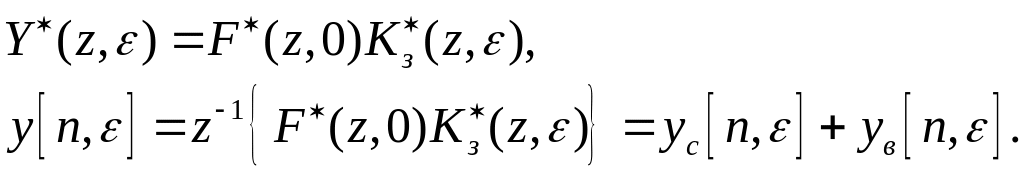
В установившемся режиме выходной сигнал определяется выражением

.

9.6 Устойчивость замкнутых систем прерывистого регулирования

9.6.1 Требования к корням характеристического полинома

Для устойчивости системы необходимо и достаточно, чтобы

.

Установим требования к корням характеристического полинома в области безразмерного преобразования Лапласа . Найдя корни характеристического полинома решётчатую функцию можно записать в виде .

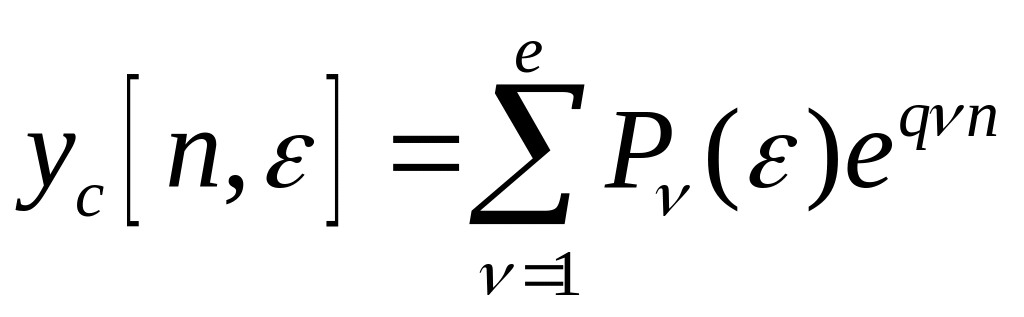В общем случае ,

где - нормированная частота, изменяющаяся от 0 до ,

- период дискретизации.

Для устойчивости системы необходимо, чтобы реальная часть корня была отрицательной

.

Так как изменяется от 0 до мнимая часть корней должна лежать в диапазоне от до .

Для устойчивости замкнутой системы прерывистого регулирования необходимо и достаточно, чтобы корни характеристического полинома замкнутой системы лежали в левой полуплоскости полосы

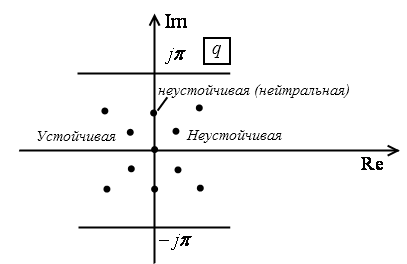
Если хотя бы один из корней лежит в правой полуплоскости, то система неустойчива. Если корни лежат на границе мнимой оси, то такая система нейтральная.

Обозначим ,

где - корни характеристического полинома замкнутой системы

.

Найдём модуль корня устойчивой системы .

Для устойчивости замкнутой системы необходимо и достаточно, чтобы все корни характеристического полинома были по модулю меньше 1 или лежали внутри круга единичного радиуса.

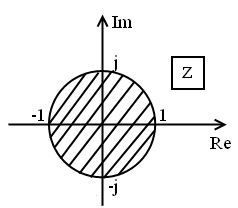
Для неустойчивой системы корни по модулю больше 1 .

Для нейтральной системы или лежат по окружности единичного радиуса.