5.2 Ошибка в течении переходного процесса (динамические ошибки)
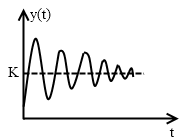
Если подать на вход системы единичный скачёк, то переходный процесс, как правило, имеет следующий вид:
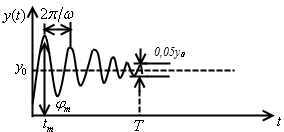
Качество переходного процесса характеризуется параметрами:
1. максимальное перерегулирование
;
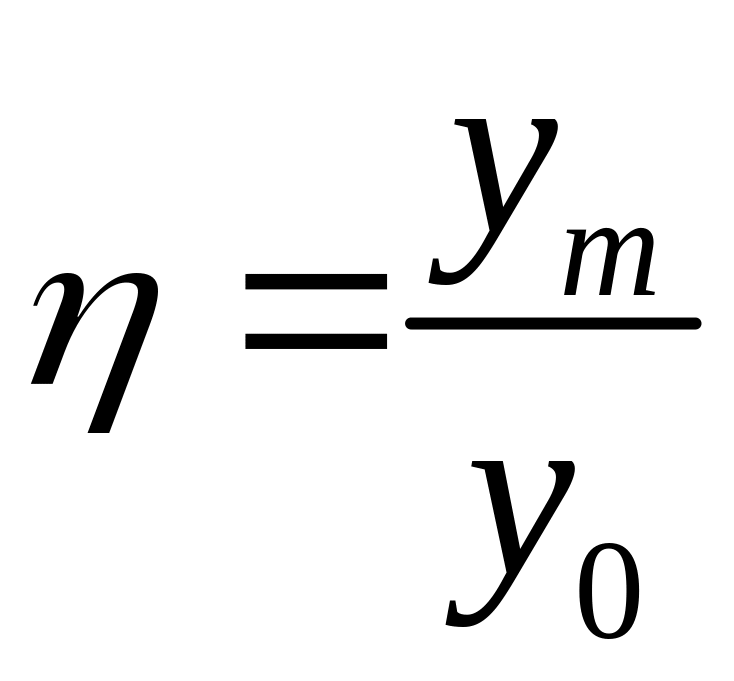2. длительность переходного
процесса
,
определяется в момент времени, когда
выходной сигнал отличается от
установившегося значения на
;
3. время достижения первого
максимума
;
4. частота автоколебаний ;
В литературе приводятся выражения для этих параметров для типичных передаточных функций.
Ошибку регулирования в переходном режиме можно определить, решая дифференциальное уравнение или используя преобразования Лапласа.
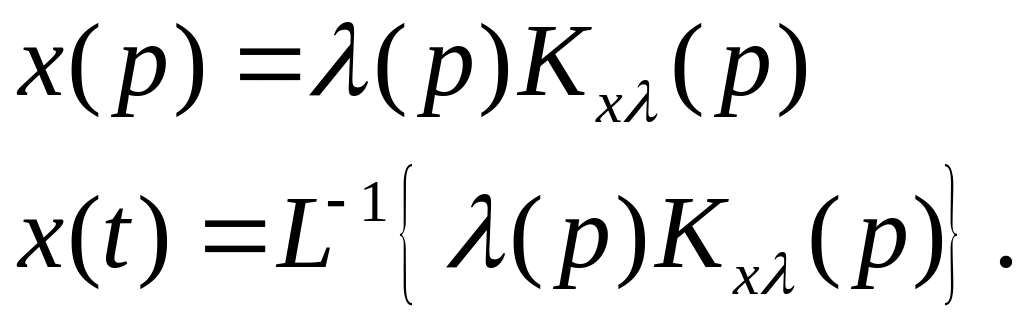
5.3 Определение показателей качества переходного процесса по лачх
Пусть задана структурная схема замкнутой системы:
;
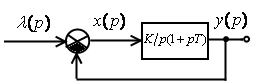
- характеристический полином;
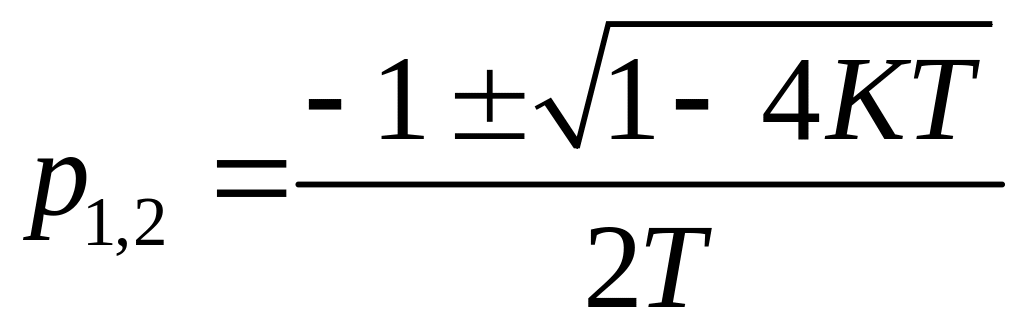- корни характеристического
полинома.
Если корни действительны
,
то выходной сигнал определяется
выражением
,
то есть является апериодическим или
экспоненциальным.
Если корни комплексные и
попарно сопряжённые
,
то выходной сигнал определяется
выражение
,
то есть выходной сигнал имеет колебательный
характер.
Рассмотрим 3 случая:
1. пусть ЛАЧХ имеет вид
,
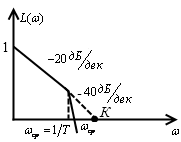
Корни являются комплексно сопряжёнными.
2. пусть ЛАЧХ имеет вид
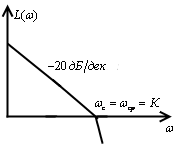
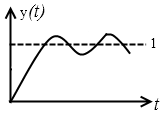
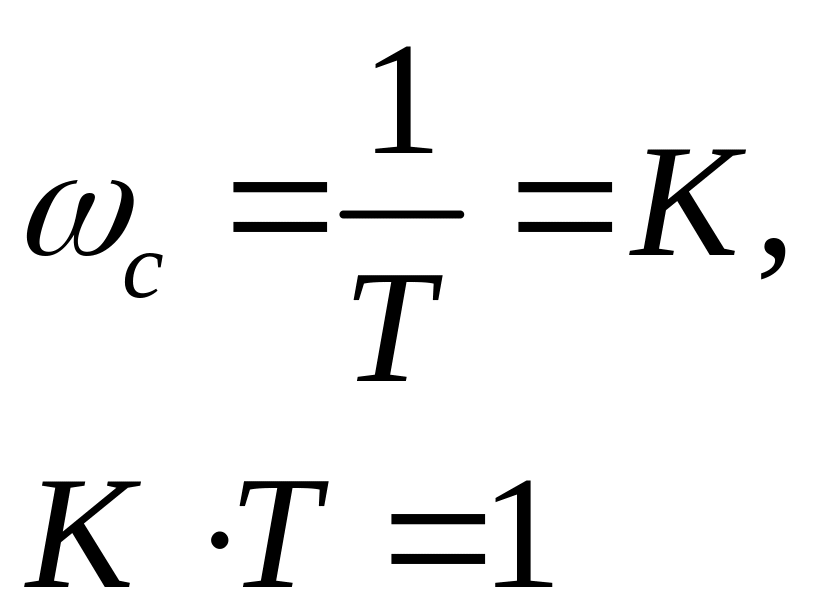
Корни комплексно сопряжённые, на частота колебаний меньше, чем в первом случае.
3. Пусть ЛАЧХ имеет вид:
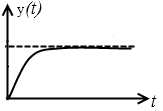
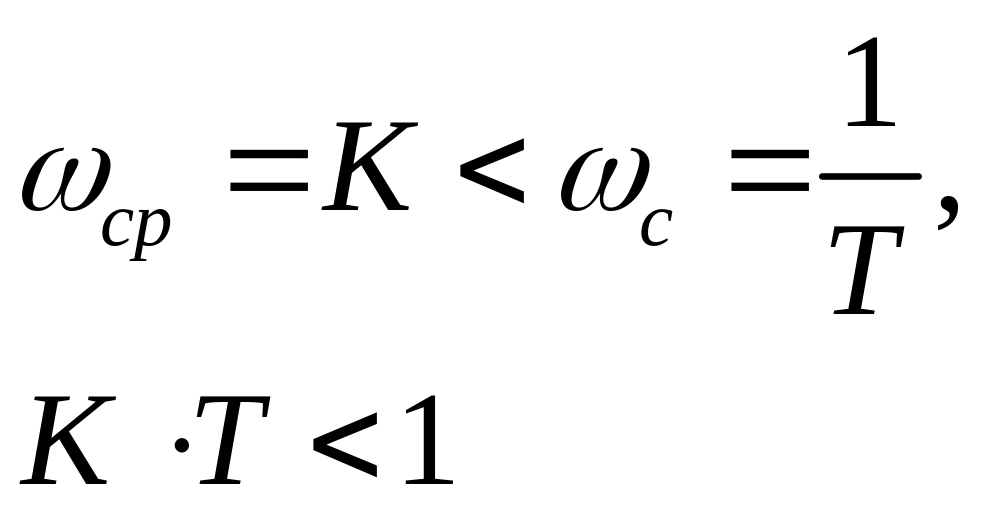
Пусть
,
корни являются действительными,
переходный процесс является апериодическим.
Чтобы переходный процесс был
близок к апериодическому необходимо,
чтобы наклон ЛАЧХ в области частоты
среза был равен
.
Причём, чем шире зона около
с наклоном
,
тем ближе переходный процесс к
апериодическому.
5.4 Анализ линейных систем методом пространства состояний
Метода пространства состояний предназначен для решения дифференциальных уравнений с помощью ЭВМ. Сущность этого метода состоит в замене скалярного дифференциального уравнения матричным дифференциальным уравнением первого порядка.
5.4.1 Краткие сведения из теории матриц
Матрица таблицы чисел содержит
строк
и
столбцов,
вида:
,
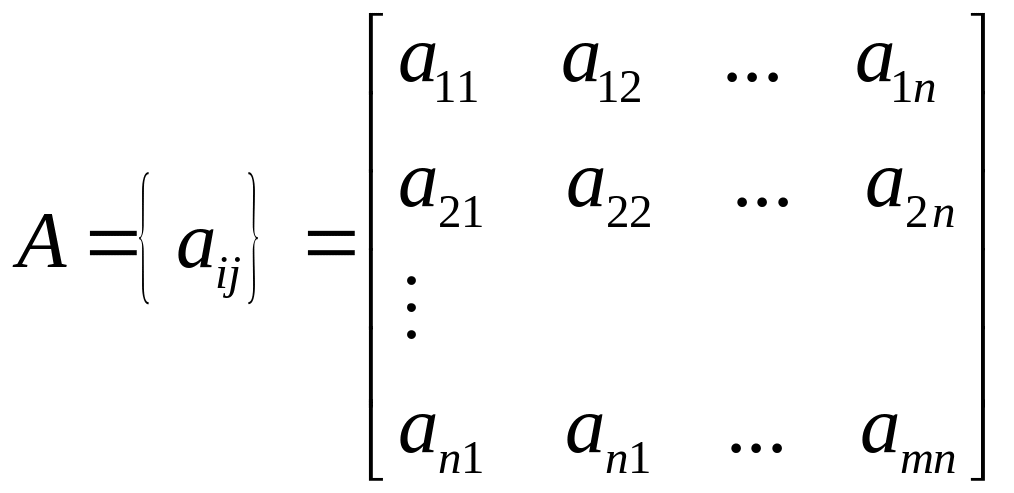где i – номер строки,
j – номер столбца.
Матрицу, состоящую из одного столбца, называют вектор-столбец, а из одной строки – вектор-строка.
Теорема сложения двух
матриц. Сумма двух
матриц
и
одинакового размера
называют матрицу
,
элементы которой равны сумме элементов
исходной матрицы
.
Теорема умножения матриц.
Произведение матрицы
размером
на матрицу
размера
называют матрицу, равной
с элементами (произведение взаимно если
)
:
.
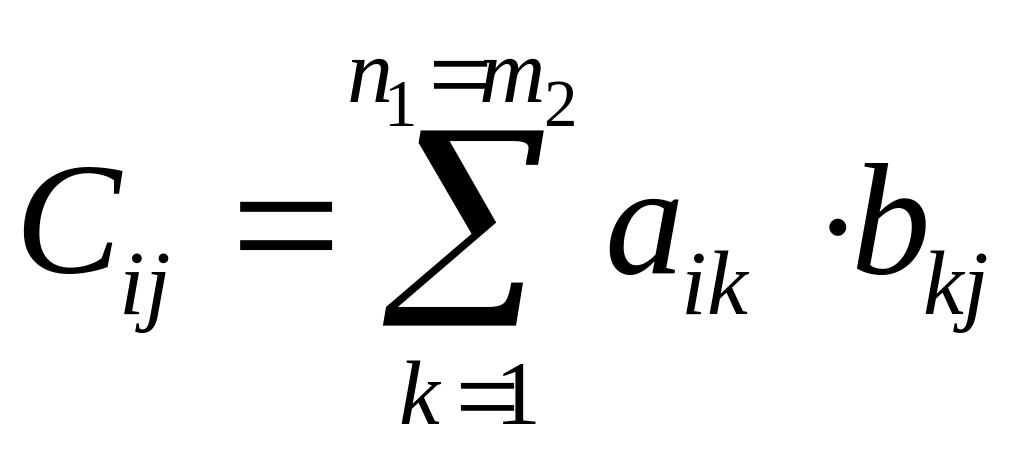Теорема обращения матрицы.
Матрица
является обратной матрице
,
если выполняется условие
- единичная матрица размером
.
,
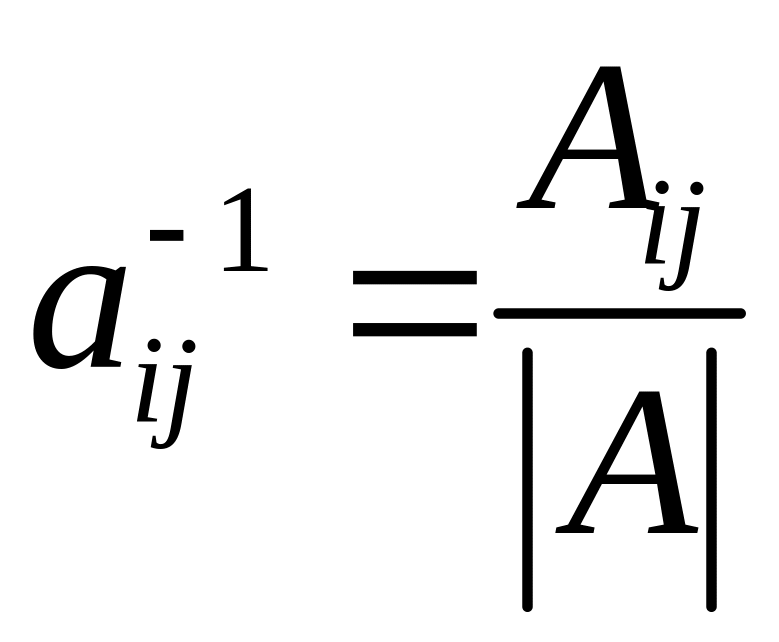где
,
такая матрица называется невырожденной,
не особенной, не сингулярной.
- алгебраическое дополнение аргумента,
где
- минор, равный определителю
порядка полученному из определителя
вычёркиванием
строки и
столбца.
Пример №1.
.
Теорема дифференцирования и интегрирования матриц. Для нахождения производной или интеграла от матрицы по скалярному аргументу необходимо вычислить их для каждого элемента матрицы.
Матричной экспонентой называют
матрицу
,
где - матрица,
- скалярный аргумент,
определяющейся бесконечным рядом
.
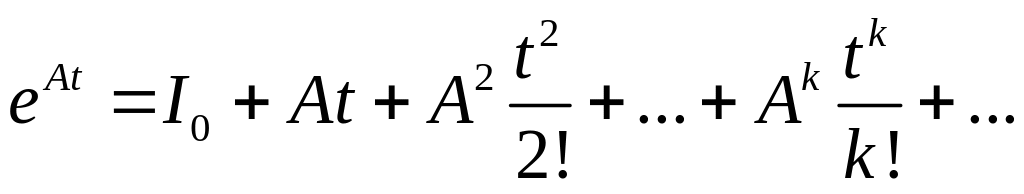