
- •Вариант № 1.
- •Вариант № 2.
- •Вариант № 3.
- •Вариант № 4.
- •Вариант № 5.
- •Вариант № 6.
- •Вариант № 7.
- •Вариант № 8.
- •Вариант № 9.
- •Вариант № 10.
- •Вариант № 11.
- •Вариант № 12.
- •Вариант № 13.
- •Вариант № 14.
- •Вариант № 15.
- •Вариант № 16.
- •Вариант № 17.
- •Вариант № 18.
- •Вариант № 19.
- •Вариант № 20.
- •Вариант № 21.
- •Вариант № 22.
- •Вариант № 23.
- •Вариант № 24.
- •Вариант № 25.
- •Вариант № 26.
- •Вариант№ 27.
- •Вариант № 28.
- •Вариант № 29.
- •Вариант № 30.
Вариант № 11.
Задача №1. Из колоды в 36 карт наугад вынимается 4. Найти вероятность того, что среди них окажется хотя бы один туз.
Ответ: 0.3895.
Задача №2. Вероятность поражения мишени при одном выстреле первым стрелком равна 0,8, вторым – 0,9. Найти вероятность того, что оба выстрела поразят мишень.
Ответ: 0,72.
Задача №3. На сборку поступают детали с двух автоматов. Первый дает в среднем 0,2% брака, второй – 0,1%. Найти вероятность попадания на сборку бракованной детали, если с первого автомата поступило 2000 деталей, а со второго – 3000.
Ответ: 0,0014.
Задача №4. Вероятность попадания в цель 0,25. Сбрасывается одиночно 8 бомб. Найти вероятность того, что будет а) не менее семи попаданий; б) не менее одного попадания.
Ответы: 0,000381; 0,8999.
Задача №5. Вероятность поражения мишени стрелком при одном выстреле равна 0,8. Найти вероятность того, что при 100 выстрелах стрелок поразит мишень ровно 75 раз. Найти наивероятнейшее число попаданий в цель. Ответы: 0,04565; 80.
Задача №6. Вероятность некоторого события в каждом испытании равна 0,4. Найти вероятность того, что: а) частота наступления события при n=1500 отклонится от р = 0,4 в ту или другую сторону меньше чем на 0,02; б) число появления события будет заключено между 600 и 660. Ответы: 0,8858; 0,4991.
Задача №7. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равна 0,0002. Найти вероятность того, что на базу поступит от 2 до 5 штук негодных изделий. Ответ: 0,2636.
Задача №8. Случайная величина Х задана законом распределения
Х |
-2 |
-1 |
0 |
1 |
2 |
Р |
0,1 |
0,2 |
0,2 |
0,4 |
0,1 |
Найти вид функции распределения случайной величины Х и построить ее график. Найти Р(|Х| ≤ 1).
Ответ: 0,8.
Задача №9. Случайная величина Х задана функцией плотности
![]()
Найти коэффициент А; M(X).
Ответы: А = 1; M(X) = 1.
Задача №10. Случайная величина Х задана функцией плотности
![]()
По какому закону распределена случайная величина? Найти M(X); D(X); σ(Х) и функцию распределения.
Вариант № 12.
Задача №1. Из полного набора костей домино наудачу берётся 5 костей. Найти вероятность того, что среди них будет хотя бы одна с шестеркой.
Указание: найти вероятность противоположного события.
Ответ: 0,7929.
Задача №2. В коробке 3 красных, 3 синих и 2 зелёных карандаша. Одновременно взято 3 карандаша. Найти вероятность того, что: а) они разного цвета; б) они одного цвета.
Ответы: 9/28; 1/28.
Задача №3. Бросают две монеты. Событие А – выпадение герба на первой монете, В – выпадение герба на второй монете, С = А + В. Найти вероятность появления события С.
Ответ: 3/4.
Задача №4. В двух ящиках находятся детали. В первом ящике 10 деталей (из них 3 стандартных), во втором – 15 (из них 6 стандартных). Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что обе детали окажутся стандартными. Найти вероятность того, что наудачу извлеченная деталь из наудачу взятого ящика будет стандартная.
Ответы: 0,12; 0,35.
Задача №5. В каждой из шести колод выбирают наудачу по одной карте. Найти вероятность того, что 4 карты окажутся красной масти, а 2 черной.
Ответ: 0,2344.
Задача №6. Производится 19 выстрелов из винтовки. Вероятность попадания в цель при каждом выстреле равна 0,8. Найти наивероятнейшее число попаданий в цель.
Ответы: 15; 16.
Задача №7. Вероятность появления события А в каждом отдельном испытании равна 0,7. Вычислить вероятность того, что при 48 независимых испытаний событие наступит ровно 30 раз; не более 30 раз.
Ответы: 0,0664; 0,1292.
Задача №8. Телефонная станция обслуживает 1000 абонентов. В данном интервале времени любой абонент независимо от остальных может сделать вызов с вероятностью 0,003. Требуется найти вероятность того, что в данном интервале было не более 5 вызовов. Ответ: 0,9161.
Задача №9. Стрелок делает по мишени три выстрела. Вероятность попадания в мишень при каждом выстреле равна 0,3. Составить закон распределения числа попаданий.
Ответ:
-
Х
0
1
2
3
Р
0,343
0,441
0,189
0,027
Задача №10. Случайная величина Х задана функцией плотности
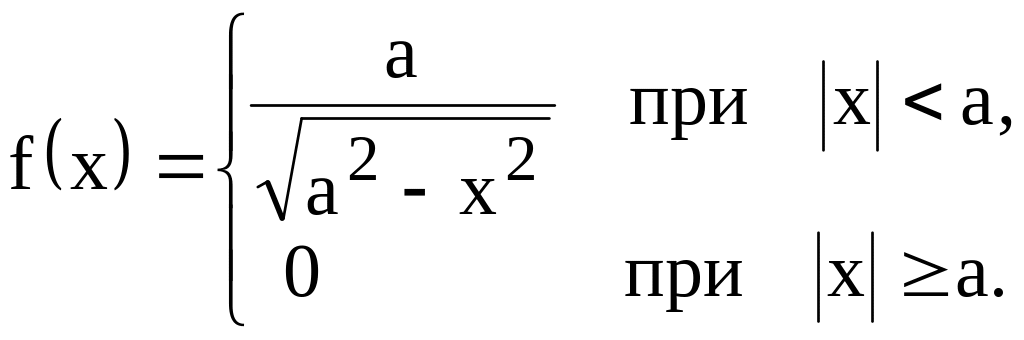
Найти: а) коэффициент а; б) Р(а/2 < Х < а).
Ответы: а = 1/π; Р(а/2 < Х < а) = 1/3.
