
- •Вариант № 1.
- •Вариант № 2.
- •Вариант № 3.
- •Вариант № 4.
- •Вариант № 5.
- •Вариант № 6.
- •Вариант № 7.
- •Вариант № 8.
- •Вариант № 9.
- •Вариант № 10.
- •Вариант № 11.
- •Вариант № 12.
- •Вариант № 13.
- •Вариант № 14.
- •Вариант № 15.
- •Вариант № 16.
- •Вариант № 17.
- •Вариант № 18.
- •Вариант № 19.
- •Вариант № 20.
- •Вариант № 21.
- •Вариант № 22.
- •Вариант № 23.
- •Вариант № 24.
- •Вариант № 25.
- •Вариант № 26.
- •Вариант№ 27.
- •Вариант № 28.
- •Вариант № 29.
- •Вариант № 30.
Вариант № 29.
Задача №1. Библиотечка состоит из десяти различных книг, причем пять книг стоят по 4 рубля каждая, три книги – по одному рублю и две книги – по 3 рубля. Найти вероятность того, что взятые две книги стоят 5 рублей. Ответ: 1/3.
Задача №2. В студии телевидения 3 телевизионные камеры. Для каждой камеры вероятность того, что она включена в данный момент, равна 0,6. Найти вероятность того, что в данный момент включена хотя бы одна камера. Ответ: 0,936.
Задача №3. В первом ящике содержится 20 деталей, из них 15 стандартных; во втором – 30 деталей, из них 24 стандартных; в третьем – 10 деталей, из них 6 стандартных. Найти вероятность того, что наудачу извлеченная деталь из наудачу взятого ящика будет стандартная. Ответ: 43/60.
Задача №4. Произведено 8 независимых испытаний, в каждом из которых вероятность появления события А равна 0,1. Найти вероятность появления события А хотя бы 2 раза.
Ответ: 0,19.
Задача №5. Найти вероятность того, что событие А наступит ровно 80 раз при 400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,2.
Ответ: 0,0498.
Задача №6. Вероятность поражения мишени стрелком при одном выстреле равна 0,75. Найти вероятность того, что при 100 выстрелах мишень будет поражена не более 70 раз.
Ответ: 0,1251.
Задача №7. Сколько раз надо бросить монету, чтобы с вероятностью 0,6 можно было ожидать, что отклонение относительной частоты появления герба от вероятности р = 0,5 окажется по абсолютной величине не более 0,01? Ответ: n = 1764.
Задача №8. Рукопись объемом в 1000 страниц машинописного текста содержит 1000 опечаток. Найти вероятность того, что наудачу взятая страница содержит: а) хотя бы одну опечатку; б) ровно 2 опечатки. Предполагается, что число опечаток распределено по закону Пуассона. Ответы: 0,6321; 0,18395.
Задача №9. Дискретные случайные величины Х и У заданы законами распределения
Х |
1 |
2 |
р |
0,2 |
0,8 |
и
У |
0,5 |
1 |
р |
0,3 |
0,7 |
Найти математическое ожидание суммы Х + У двумя способами: а) составив закон распределения Х+У; б) пользуясь свойством математического ожидания M(X+Y)=M(X)+M(Y). Ответ: M(X+Y)=2,65.
Задача №10. Случайная величина задана функцией плотности
Найти: а) функцию распределения; б) вероятность того, что в результате испытания случайная величина примет значение, заключенное в интервале (0; π/4).
Ответы: Р(0 < Х <
π/4) =
![]() ;
;
Вариант № 30.
Задача №1. В мешочке имеется 5 одинаковых кубиков. На всех гранях каждого кубика написана одна из следующих букв: о, п, р, с, т. Найти вероятность того, что на вынутых по одному и расположенных «в одну линию» кубиках можно будет прочесть слово «спорт».
Ответ: 1/120.
Задача №2. В типографии имеется 4 плоскопечатных машины. Для каждой машины вероятность того, что она работает в данный момент, равна 0,9. Найти вероятность того, что в данный момент работает хотя бы одна машина. Ответ: 0,9999.
Задача №3. В двух ящиках имеются радиолампы. В первом ящике содержится 12 ламп, из них 1 нестандартная; во втором – 10 ламп, из них 1 нестандартная. Из первого ящика наугад взята лампа и переложена во второй. Найти вероятность того, что наудачу извлеченная из второго ящика лампа будет нестандартной. Ответ: 13/132.
Задача №4. Монету бросают 6 раз. Найти вероятность того, что герб выпадет: а) менее двух раз; б) не менее двух раз. Ответы: 7/64; 57/64.
Задача №5. Найти приближенно вероятность того, что при 400 испытаниях событие наступит ровно 104 раза, если вероятность его появления в каждом испытании равна 0,2.
Ответ: 0,0006.
Задача №6. Вероятность поражения мишени стрелком при одном выстреле равна 0,75. Найти вероятность того, что при 100 выстрелах мишень будет поражена не менее 70 раз и не более 80 раз. Ответ: 0,7498.
Задача №7. Вероятность появления события в каждом из независимых испытаний равна 0,2. Какое отклонение относительной частоты появления события от его вероятности можно ожидать с вероятностью 0,9128 при 5000 испытаниях? Ответ: 0,00967.
Задача №8. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равна 0,0002. Найти вероятность того, что на базу прибудут 3 негодных изделия. Ответ: 0,06.
Задача №9. Дискретные независимые случайные величины заданы законами распределения
Х |
1 |
2 |
Р |
0,2 |
0,8 |
и
У |
0,5 |
1 |
Р |
0,3 |
0,7 |
Найти математическое ожидание ХУ двумя способами: а) составив закон распределения ХУ; б) пользуясь свойством математического ожидания М(ХУ)=M(X)M(Y).
Ответ: 1,53.
Задача №10. Случайная величина Х задана функцией распределения
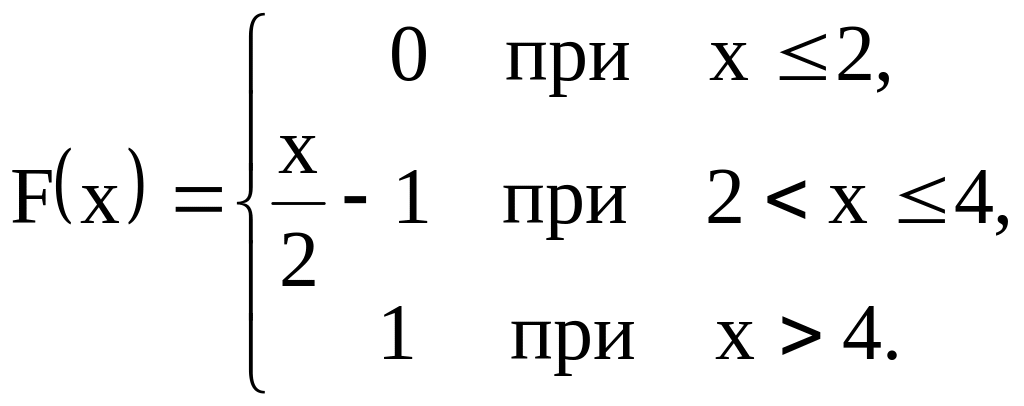
Найти вероятность того, что в результате испытания Х примет значение, заключенное в интервале (2; 3).
Ответ: 1/2.
