
- •Курсовая работа
- •Содержание
- •Раздел 1. Система Ляпунова ─ случай одной степени свободы………….......4
- •Раздел 2. Условия существования периодических решений.…………..…..10
- •Раздел 3. Метод Ляпунова. ………………………………………………………13
- •Введение.
- •Теоретическая часть
- •Раздел 1. Система Ляпунова ─ случай одной степени свободы. Система Ляпунова.
- •Приведение к каноническому виду.
- •Преобразование интеграла h.
- •Периодичность решений системы Ляпунова.
- •Теорема Ляпунова.
- •Теорема Ляпунова.
- •Раздел 2. Условия существования периодических решений Необходимые и достаточные условия периодичности.
- •Раздел 3. Метод Ляпунова. Алгоритм.
- •Практическая часть Индивидуальное задание Список литературы.
Теорема Ляпунова.
Теперь вычислим период, для этого составим дифференциальные уравнения, которым удовлетворяют переменные ρ и θ. Вычислим
![]() (1.15)
(1.15)
Заменяя
в системе (1.15) производные
![]() и
и
![]() их выражениями из уравнений (1.8) и разрешая
полученную систему относительно
производных
и
,
найдем искомые уравнения
их выражениями из уравнений (1.8) и разрешая
полученную систему относительно
производных
и
,
найдем искомые уравнения
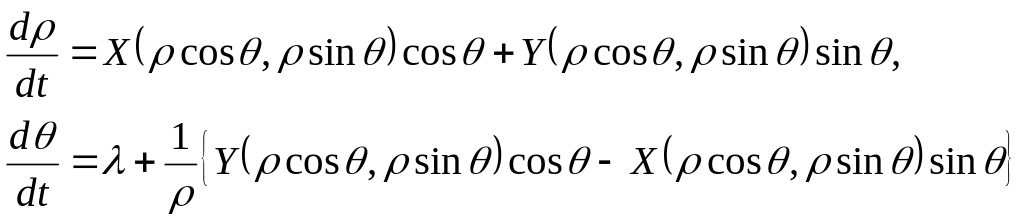 (1.16)
(1.16)
Из второго уравнения определим t:
![]() (1.17)
(1.17)
Для того чтобы удовлетворить условиям (1.13), необходимо константу (1.17) принять равной нулю. Используем тот факт, что ρ - аналитическая функция μ. Это позволит разложить подынтегральную функцию в выражении (1.17) в ряд по степеням μ
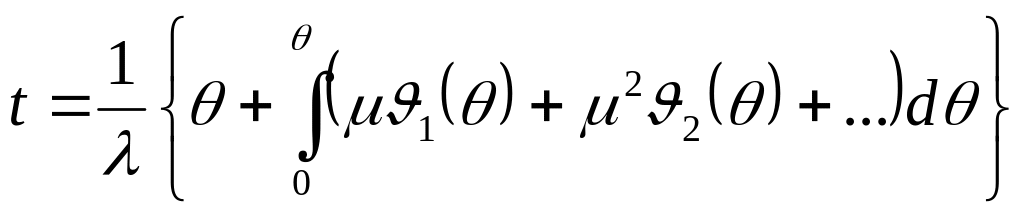 (1.17’)
(1.17’)
где
![]() - периодические функции θ периода 2π.
Следовательно, подынтегральная функция
в (1.17’) также
периодическая
функция
θ периода 2π. Следовательно,
интеграл
- периодические функции θ периода 2π.
Следовательно, подынтегральная функция
в (1.17’) также
периодическая
функция
θ периода 2π. Следовательно,
интеграл
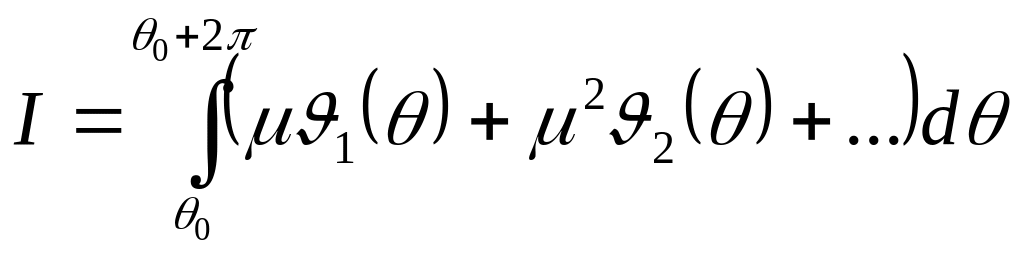
не зависит от θ0 и его можно записать в виде
![]() ,
,
где
![]() - вполне определенные числа. Таким
образом, при измени θ
на 2π время t
получает приращение Т
- вполне определенные числа. Таким
образом, при измени θ
на 2π время t
получает приращение Т
![]() ,
(1.18)
,
(1.18)
не зависящие от θ0.
Пусть теперь Ф(θ) – некоторая периодическая функция θ периода 2π, тогда
![]() .
(1.19)
.
(1.19)
Рассматривая ее как функцию t, будем иметь
![]() .
(1.20)
.
(1.20)
Равенство (1.19) справедливо для любых θ, следовательно, и равенство (1.20) справедливо для любых t, т. е. Ф(t) – периодическая функция t. Значит, величина Т, определенная формулой (1.18) как функция μ, и есть период решения.
Используя (1.17), мы можем записать его в следующем виде:
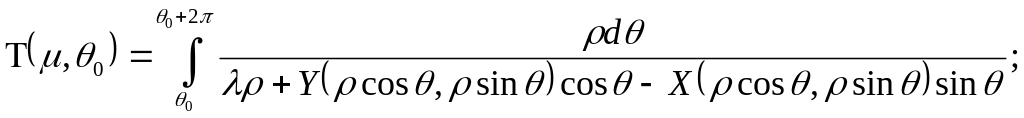
где
![]() период Т стремится к периоду линейных
колебаний 2π/λ, т. е. к периоду колебаний
в системе (1.8) при
период Т стремится к периоду линейных
колебаний 2π/λ, т. е. к периоду колебаний
в системе (1.8) при
![]() .
.
Покажем теперь, что Т- четная функция μ. Вернемся сова к интегралу (1.11). рассматривая его как уравнение относительно ρ, мы получаем в окрестности точки ρ=0 два решения. Одно из них
![]() (1.21)
(1.21)
другое
![]() (1.21’)
(1.21’)
Теперь заметим, что левая часть уравнения (1.11) не изменится, если заменим ρ на -ρ и θ на θ + 2π. Следовательно, на основании (1.21) будем иметь
![]() (1.22)
(1.22)
Значение ρ, определенное рядом (1.22), будет корнем уравнения (1.11), не совпадающее с (1.21) (потому, что для малых ρ из (1.21) следует ρ = μ+О(μ2), а из (1.22) ρ = - μ+О(μ2)). Следовательно, оно будет определяться рядом (1.21’).
Сравнивая (1.21’) и (1.22), получаем
![]()
и т.д.
Отсюда следует, что если в выражении (1.21) заменить μ на – μ, а θ на θ + π, то величина ρ примет свое значение с обратным знаком:
![]() .
.
Выпишем теперь выражение для периода Т. На основании (1.17) имеем
![]() .
(1.23)
.
(1.23)
Сделаем замену в (1.23) замену μ на –μ, а θ на θ + π. Тогда получим величину
![]() .
.
Согласно
доказанному величины
![]() и
и
![]() сохраняют свои значения. Следовательно,
то же самое можно сказать и о функциях
Х и Y. В то же время
сохраняют свои значения. Следовательно,
то же самое можно сказать и о функциях
Х и Y. В то же время
![]() ,
,
![]() и
и
![]() изменяют свои знаки. Следовательно,
знаменатель изменит знак на обратный,
но и числитель изменит знак на обратный.
Следовательно,
изменяют свои знаки. Следовательно,
знаменатель изменит знак на обратный,
но и числитель изменит знак на обратный.
Следовательно,
![]() .
.
Итак,
![]() ,
,
т. е. период – четная функция величины μ.
Таким образом, выше было доказано теорему Ляпунова, а теперь сформулируем ее.
Теорема Ляпунова.
Если
постоянная
достаточно мала, то все решения системы
уравнения (1.8) ─ периодические функции
t
, причем период ─ четная функция величин
и при
![]() стремится к
стремится к
![]() .
Решения системы (1.8) являются аналитическими
функциями величины c
─ начального отклонения переменной x
.
.
Решения системы (1.8) являются аналитическими
функциями величины c
─ начального отклонения переменной x
.
Имея
в виду формулу
![]()
выражение периода можно переписать в следующем виде:
![]() (1.24)
(1.24)
