5. Интервал и причинность

Интервалом называется характеристика для двух любых событий, которая определяется так:

Интервал является кривой, не зависящей от системы отсчёта, то есть интервал инвариантная величина. Рассмотрим частные случаи

1) > 0. Это возможно, когда пространственные координаты не вносят существенного вклада в величину интервала. Такой интервал называется времени подобным.

2) < 0 пространственные координаты вносят существенный вклад в величину интервала. Такие интервалы называются пространственно подобными

3) 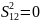пространственные и временные координаты вносят одинаковый вклад. Такие интервалы называются нулевыми или световыми.

Установим причинно – следственную связь между событиями. Если информация приходит в некоторую точку, то эта точка является следствием, какого-то события. Пусть мы рассматриваем точку 1, и все события рассматриваем относительно неё. Данная фигура - трёхмерный конус в четырёхмерном пространстве. Нижняя часть конуса является областью абсолютного прошлого конуса. Верхняя его часть называется областью абсолютного будущего. Область вне конуса называется абсолютно удалённой. Событие 1 – следствие любого из событий снизу и причина любого из событий сверху.

Для любого события внутри конуса интервал является времениподобным, вне конуса по отношению к 1 – пространственноподобным.

_______________________________________

10. Калибровочная инвариантность. Функция Гамильтона.

Для того, чтобы найти вектор электрического поля, мы должны, исходя из уравнения движения, поместить частицу в поле и измерить силу

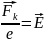
Второй шаг – измеряем силу, действующую на неподвижную частицу, вычитаем кулоновскую силу, => определяем вектор .

Это главный и единственный способ определения и . Вернемся к определению полей и через и . Через эти опр-ния не видно прямого способа измерения и .

Если и измеримы, то можно ли восстановить и по этим векторам?

Да, можно восстановить, но неоднозначно.

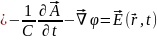
Мы убедились, что потенциалы определены неоднозначно.

Преобразование потенциалов, не изменяющее векторов поля называется калибровочным преобразованием или градиентным преобразованием.

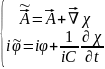
Принцип калибровочной инвариантности:

Всякое математическое выражение, описывающее измеряемые характеристики электромагнитного поля, не должно меняться при калибровочных преобразованиях потенциалов.

- энергия частицы во внешнем поле. Она состоит из энергии свободной частицы и энергии воздействия поля.

11. Тензор эмп.

Если мы покоимся в системе, то на нее не действуют силы. Если же мы находимся в движущейся системе, то

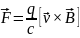
Необходимо найти инвариантное написание четырехмерной формы для электромагнитного поля.

Получим четырехмерный объект, описывающий четырехмерное поле.

Вернемся к рассмотрению заряженной частицы во внешнем элементарном поле. Повторим вывод в четырехмерной форме.

Если выбранная траектория истина, то действие по очень близкой траектории будет больше. - вариация траектории.

Вариация действия вдоль истиной траектории равна нулю. Раз это справедливо, воспользуемся этим.

Домножим на :

Продифиринцируем это выражение:

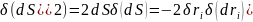
Под знаком интеграла останется:

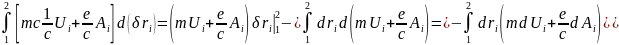
Так как

- функция, которая зависит от координат радиус-вектора.

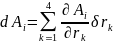
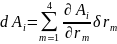
Подставим данные записи в исходный интеграл, получим:

произведем замену: :

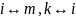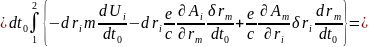
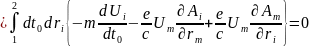
(четырехмерное обобщение уравнения движения частицы в поле)

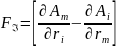
(характеристическое силовое воздействие поля, тензор эл.маг. поля)

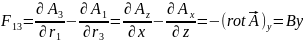
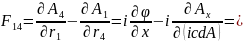
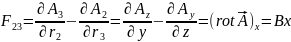
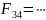
Эл.маг. поле опр-ся так же как и тензор , точнее как его проекция на оси в выбранной системе координат. Для полного определения поля необходимо определить и эл. и маг.поле – это единый объект.

_______________________________________
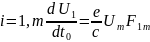
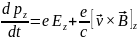
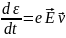