
- •2. Сокращение масштабов, собственное время.
- •3. Преобразование скорости и аберрации света
- •4. Геометрический смысл преобразования Лоренца.
- •14. Уравнение электромагнитного поля. Первая пара уравнений Максвелла.
- •6. Четырехмерные векторы, тензоры и скорости.
- •9. Уравнения движения заряда в эмп.
- •7. Принцип наименьшего действия.
- •5. Интервал и причинность
- •10. Калибровочная инвариантность. Функция Гамильтона.
- •11. Тензор эмп.
- •13. Инварианты электромагнитного поля.
- •12. Преобразование Лоренца для электромагнитного поля.
- •1. Основные постулаты сто. Преобразования Лоренса
9. Уравнения движения заряда в эмп.
Поставим задачу: как движется заряженная частица во внешнем ЭМП?
Рассмотрим уравнение движения частицы. Запишем уравнение Лагранжа.
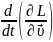 -
-
 = 0
= 0
Подставим конкретный вид функции Лагранжиана в уравнение:
 =
=
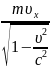 +
+
 =
=




 =
=
 =
=
 +
+

где – обобщенный импульс;
Для частицы во внешнем поле обобщенный импульс не совпадает с самим импульсом частицы.
Найдем полную производную по времени от обобщенного импульса:

 =
=
 +
+

т.к.
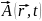 =
=


Вычислим производную Лагранжа по координате:
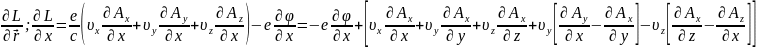
 -
-
 z
z
 -
y
-
y
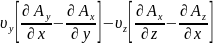 –
–
 x
x



Объединим в одно уравнение:
 -
-

Поставим следующую задачу: нам известно φ, и е. Нам нужно найти импульс и скорость.
Таким
образом, последнее уравнение – ду одной
переменной (векторной величины)
и
 .
.

Первое слагаемое данного уравнения зависит только от поля. Правая часть – это силы, действующие на частицу со стороны заданного эмп.
Принято использовать следующие обозначения для величин, входящих в правую часть.

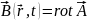
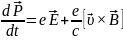
Принято
называть вектора
 и
и
 ,
векторами напряженности электрического
поля и вектором магнитной индукции
соответственно.
,
векторами напряженности электрического
поля и вектором магнитной индукции
соответственно.
Вектора и описывают свойства эмп и являются двумя частями одного целого.
7. Принцип наименьшего действия.
Для каждой физической системы мы можем ввести функцию Лагранжа, описывающую эволюцию системы:

![]()
Ставится задача: как выбрать истинную траекторию.
Введем понятие принципа наименьшего действия (ПНД):
 – действие
вдоль траектории.
– действие
вдоль траектории.
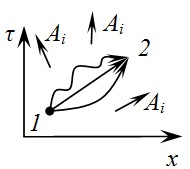
Истинная траектория между точками 1 и 2 - это та траектория, действие вдоль которой минимально.
При переходе к четырехмерному пространству формулировка ПНД не меняется. Траектория – мировая линия.
Рассмотрим пустое пространство и свободную частицу. Лагранжиан такой частицы:
 ,
траектория – прямая линия.
,
траектория – прямая линия.
Сформулируем дополнительное условие на ПНД исходя из равноправности систем отсчета: действие должно быть скалярным.
Траектория также не должна изменяться из одной ИСО в другую ИСО.




Найдем выражение Лагранжиана для свободной частицы в четырехмерном пространстве и времени.

Разобьем траекторию на маленькие интервалы dS.
inv характеристика траекторий длина

 – не
меняет сущности действия
– не
меняет сущности действия



При V 0 и разложив это выражение в ряд

Можно потребовать, что на малых скоростях Лагранжиан должен преобразовываться к классическому виду.
Множитель αc = const – соответственно
 ,
,
 =>
=>
 – релятивистское
выражение для Лагранжиана свободной
частицы.
– релятивистское
выражение для Лагранжиана свободной
частицы.
Соответственно, зная функцию Лагранжа, можно установить характеристики частиц при любых скоростях.
 ,
,
 ,
,
 =
=
 ,
,
 =
=
 =
=
 ,
,
 =
=
 =
=
 ,
,
 =
=
 =
=
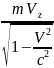
=

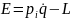
 +
+
 +
+
 - L =
+ m
- L =
+ m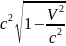 = E =
= E =
 =
=

E =
При скорости движения равной нулю, любая частица обладает энергией (энергия покоя).
 =
=
 - формула Эйнштейна, это есть следствие
инвариантности ПНД.
- формула Эйнштейна, это есть следствие
инвариантности ПНД.
Если
скорость частицы отлична от нуля, то
полная энергия
 .
.
Из выражения для импульса и энергии частицы можно выразить связь между p и E.

Это выражение позволяет вычислить импульс частицы без массы, то есть если объект обладает энергией, то он обладает и импульсом.
Приведем рассмотренные величины к четырехмерной форме записи.
=
m
= ( )
)

Четвертой
компонентой импульса является энергия,
поэтому
 энергии.
энергии.
В четырехмерном мире нельзя рассматривать отдельно импульс и энергию, так как они являются компонентами одного вектора:
=

=
γ(
- i ),
=
),
=
 ,
=
,
=
 ,
,
 = γ(i
= γ(i +
+
 )
)
=
γ( - i
- i )
= γ(
+
)
= γ(
+
 )
)
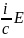 =
γ(
=
γ( +
+
 )
=> E=γ(V
+ E’)
)
=> E=γ(V
+ E’)
Алгоритм отыскания преобразования величины при переходе из одной ИСО в другую:
1. Определение трехмерной величины как четырехмерной
2. Применение преобразования
3. Раскрытие индексной формы записи
Найдем четырехмерную функцию Гамильтона:
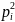 =
=
 =
=
 = -m
= -m =
=
 +
+
 +
+
 +
+
 =
=
 -
-

 =
=
 +
+


_______________________________________
8. 4-x мерный потенциал
Перейдем к описанию электрических явлений. ЭМП р/м как самостоятельно существующий объект. Для выявления существования поля проведем мысленный эксперимент.
![]()
Частицы движутся равномерно. Относительно движущейся системы события в точке А и В будут неодновременными. С точки зрения движущегося наблюдателя события в точке А наступит раньше, чем в В |=> в какой-то момент времени первая частица будет двигаться без ускорения, а вторая ускоренно |=> изменится импульс системы на некотором промежутке времени |=> нарушается закон сохранения импульса (этого быть не должно) |=> в нашей системе чего-то нахватает.
Способ разрешения парадокса - предположение существования 3-го объекта – ЭМП. Данный прим. показывает, что ЭМП существует как самостоятельный объект. Заряженные частицы никогда не взаимодействуют друг с другом. Они всегда взаимодействуют с полем.
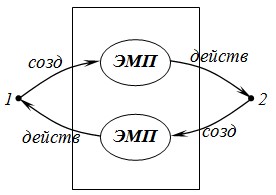
Каковы
обобщенные координаты ЭМП? Обобщение
большого количества материальных
факторов приводит к утверждению, что
заряд частицы полностью описывает
эл.маг. свойства этой частицы.
Заряд - это скаляр инвариант. ЭМП полностью и однозначно описывается 4-х вектором Ai(ri). Этот вектор мы будем называть 4-х мерным потенциалом ЭМП. Ai – принадлежит всему пространству.
Обратимся
к принципу наименьшего действия.
Действие для частицы, находящейся в
ЭМП, можно описать как
 .
Где
.
Где
 - действие свободной частицы,
- действие свободной частицы, – взаимодействие частицы и поля
– взаимодействие частицы и поля

 предполагается
что
- заданная величина.
предполагается
что
- заданная величина.
При
наличии поля лучшей траекторией будет
не прямая, а кривая. Это обусловлено
существованием потенциала

Исходя из этих позиций найдем функцию Лагранжа для частицы во внешнем ЭМП.




Обобщим полученный результат:


