
- •2. Сокращение масштабов, собственное время.
- •3. Преобразование скорости и аберрации света
- •4. Геометрический смысл преобразования Лоренца.
- •14. Уравнение электромагнитного поля. Первая пара уравнений Максвелла.
- •6. Четырехмерные векторы, тензоры и скорости.
- •9. Уравнения движения заряда в эмп.
- •7. Принцип наименьшего действия.
- •5. Интервал и причинность
- •10. Калибровочная инвариантность. Функция Гамильтона.
- •11. Тензор эмп.
- •13. Инварианты электромагнитного поля.
- •12. Преобразование Лоренца для электромагнитного поля.
- •1. Основные постулаты сто. Преобразования Лоренса
4. Геометрический смысл преобразования Лоренца.
Любая точка в 4-хмерном мире характеризуется четырьмя числами (x,y,z,t).
При описании событий мы используем числовые значения.
Мировая линия – совокупность последовательных событий.
![]()
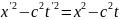
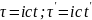
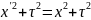
При переходе в другую систему отсчета квадрат расстояния не меняется.
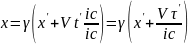
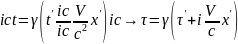
![]()
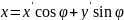
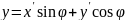
Введем
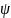 ,
тогда:
,
тогда:
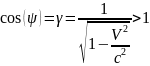
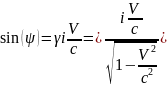
В плоскости xτ преобразование Лоренца соответствует повороту системы координат на псевдо-угол ψ.


Переход от покоящейся к движущейся системе отсчета в 4-хмерном мире соответствует повороту. При повороте не изменяется и расстояние между 2-мя точками (событиями).

Если рассматривать события 1 и 2, то расстояние между ними не изменяется.
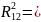
Рассмотрим релятивистские эффекты
1) Понятие одновременности событий
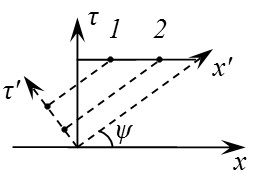
В новой системе отсчета события уже не одновременные
2) Эффект сокращения длины
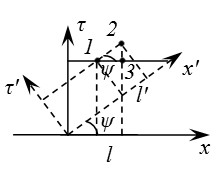
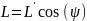 ;
;
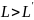
3) Эффект замедления времени

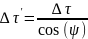 ;
;
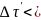
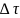
4) Если скорость относительного движения сонаправлена с осью y, то такому движению будут соответствовать поворот оуτ.
Результат 2-х последовательных переходов – 2 поворота плоскостей. Результат зависит от порядка выполнения перехода.
Преобразование Лоренца некоммутативное. Исключение: составное движение производится вдоль одной оси.
_______________________________________
14. Уравнение электромагнитного поля. Первая пара уравнений Максвелла.
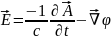
Уравнение электромагнитного поля
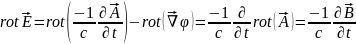

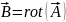
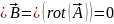 – поле
соленоида
– поле
соленоида


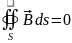
Поток вектора В через любую замкнутую поверхность равен нулю
![]()
6. Четырехмерные векторы, тензоры и скорости.
Все физические величины, законы, формулируются в векторной или тензорной форме. Объяснением этому служит то, что векторная или тензорная форма указывает на тот факт, что величина не привязана к системе координат. Так как пространство 4-мерное, то необходимо пересмотреть все физические законы на 4-мерное представление. Введем понятие 4-мерного вектора:
![]()
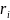 – четырех-радиус-вектор.
– четырех-радиус-вектор.
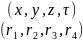
Запишем преобразование Лоренца для 4-вектора.
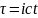
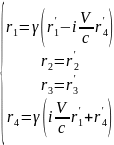
 =(
=(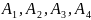 )
– 4-вектор
как совокупность 4-ех величин в некоторой
системе отсчета, которые при переходе
к другой системе отсчета преобразуются
так же, как и компоненты 4-ех радиус-вектора.
)
– 4-вектор
как совокупность 4-ех величин в некоторой
системе отсчета, которые при переходе
к другой системе отсчета преобразуются
так же, как и компоненты 4-ех радиус-вектора.

Основное свойство вектора: инвариантность относительно системы координат сохраняется для 4-вектора. Но его проекция на оси является инвариантной величиной. Соотношения между векторами также инвариантны, так как все вектора преобразуются по одинаковой схеме. Вектор - это тензор первого ранга, скаляр - это тензор нулевого ранга (величина, неизменная при любых преобразованиях координат).
Скалярное произведение 2-ух 4-векторов инвариантно:
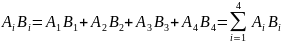
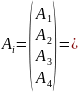
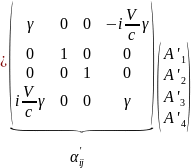
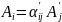 -
запись Эйнштейна
-
запись Эйнштейна
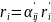 -
преобразование
для радиус-вектора
-
преобразование
для радиус-вектора
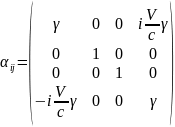
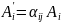
4-ех
тензор второго ранга ( )
- совокупность 16 компонент, образующихся
как произведение компонент векторов;
)
- совокупность 16 компонент, образующихся
как произведение компонент векторов;
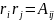

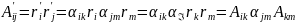
Единичный
4-ех тензор:
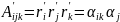 A
A
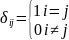

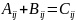

(1) - тензор второго ранга,
(2) - 4-ех тензор третьего ранга,
(3) - 4-ех тензор четвертого ранга.
Свертка:
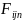 – 4-ех тензор третьего ранга
– 4-ех тензор третьего ранга
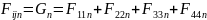
1. grad
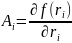 скалярная
функция 4-ой точки пространства
скалярная
функция 4-ой точки пространства
2. div
f - скалярная (инвариантная) величина
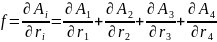 -
4-ех мерная дивергенция
-
4-ех мерная дивергенция
3. rot
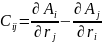
4. Оператор Лапласа
 -
скалярная функция
-
скалярная функция
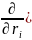 )
=
)
=
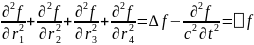 – оператор Даламбера
– оператор Даламбера
Все вышеописанные операции являются тензорными и, следовательно, инвариантными. Таким образом, результат этих операций будет для всех одинаковым.
Пример 4-ех мерной скорости:
![]()
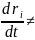 т.к.
скорость в 4-ех мерном пространстве
определить нельзя, так как время не
является тензорной величиной в этом
случае;
т.к.
скорость в 4-ех мерном пространстве
определить нельзя, так как время не
является тензорной величиной в этом
случае;
 ,
- собственное время
,
- собственное время
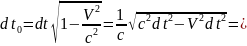
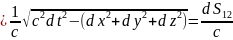
Выразим
компоненты 4-ех скорости
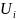 через
3-ех мерный вектор скорости:
через
3-ех мерный вектор скорости:
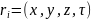 ,
,
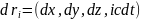
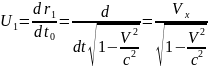

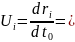 ;
;
 ;
;
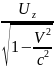 ;
;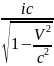 ) =
;
) =
;
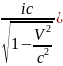
Свойства 4-ех вектора скорости.
Возьмем
модуль: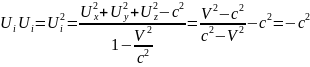
 ,
вектор 4-ех скорости меняется только
за счет направления, а его величина
остается постоянной.
,
вектор 4-ех скорости меняется только
за счет направления, а его величина
остается постоянной.
Определим
4-ех ускорение:
 ,
так как длина вектора скорости не
изменяется, то 4-ех ускорение всегда
ортогонально 4-ех скорости → скалярное
произведение скорости на ускорение
равно 0.
,
так как длина вектора скорости не
изменяется, то 4-ех ускорение всегда
ортогонально 4-ех скорости → скалярное
произведение скорости на ускорение
равно 0.
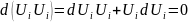 /
: d
/
: d
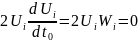
_______________________________________
