Добавление линий слияния

Первое, что необходимо сделать для более аккуратного моделирования трехмерного куба - это соединить вершины модели с помощью линий для создания каркаса. Это можно было сделать уже во Flash 5, но во Flash MX это намного проще, так как здесь можно использовать рисование API.

1. Сохраните имеющийся фильм в файле spinning_cube_1.fla. Теперь мы добавим код в нашу функцию прорисовки для рисования линий между вершинами. Для этого необходимо знать, какие вершины должны быть соединены друг с другом. Это сделать, добавив стороны к нашей модели, состоящие из выделенных вершин. Введите следующий код сразу после предыдущих строк, определяющих вершины cube (под последней строкой, начинающейся с cube.vertex.push).

2. cube, side = [];

3. cube.side.push([0, 1, 2, 3]);

4. cube.side.push([2, 1, 5, 6]);

5. cube.side.push([1, 0, 4, 5]);

6. cube.side.push([5, 4, 7, 6]);

7. cube.side.push([0, 3, 7, 4]);

8. cube.side.push([3, 2, 6, 7]);

side - это еще один параметр массива нашей модели. Каждый индекс состоит из четырех вершин, которые формируют сторону куба (попробуйте растянуть ее, чтобы увидеть, как это повлияет на связанные вершины). Порядок, в котором расположены вершины в каждом индексе side, очень важен, и вы убедитесь в этом, когда мы будем рассматривать процесс выбраковывания, заключающийся в том, что все стороны, не наблюдаемые пользователем, становятся невидимыми (это снижает загрузку процессора). Скоро мы это обсудим. А сейчас просто убедитесь в том, что вы сохранили порядок вершин для каждой стороны (порядок сторон неважен).

После удаления и переопределения нашего lineStyle проходим циклом через все наши стороны и рисуем линии между всеми вершинами. Начинаем с движения карандаша к вершине в индексе 0 нашей текущей стороны. После этого рисуем линию, соединяющую все остальные вершины на стороне, заканчивая рисованием линии к исходной вершине. Сейчас запустите ваш фильм, чтобы увидеть линии получившегося каркаса.

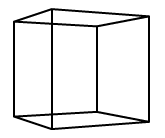
Линии, нарисованные в API, добавлены для определения граней нашей модели.

Теперь, когда есть линии каркаса, фильмы вершин стали несколько лишними. Мы можем удалить их все вместе и сделать так, чтобы вершины существовали отдельно в памяти компьютера. Нужно будет найти экранные координаты x и y вершин, не имея возможности посмотреть параметры _x и _y фильма.

Матрицы преобразования

При любом вращении по оси y (вы сами можете составить код для вращения вокруг двух других осей) мы обрабатываем циклом каждую вершину и соответствующим образом настраиваем координаты. Было бы неплохо осуществлять это только один раз, после вычисления всех необходимых преобразований. Это можно реализовать с помощью матриц.

Каждая вершина также может быть описана матрицей без надобности настройки какого-либо кода. Вершина с координатами (50,30,15) может быть записана в следующем виде:

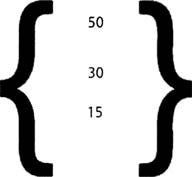
В нашем последнем упражнении, например в функции rotateY, преобразование обеспечивалось следующим образом.

x = cos(?)*x - sin(?)*z;

//У = y;

z = cos(?)*z + sin(?)*x;

Эта формула преобразования может быть сохранена в матрице преобразования, которую можно умножить на наши 3D-координаты. Эти матрицы преобразования могут быть непосредственно перемножены друг на друга, после чего получится кумулятивная матрица преобразования, и нам нужно просто провести умножение на наши координаты один раз в конце преобразований. Это помогло бы сохранить процессорное время и помочь в наших будущих преобразованиях. Итак, матрица преобразования для кода, указанного выше, выглядит так.

Результат умножения данной матрицы 3х3 на координатную матрицу 3х1 даст нам другую матрицу.

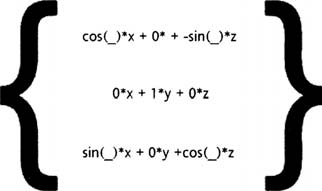
Это та же формула, которая использовалась функцией rotateY, рассмотренной выше! Может показаться, что использовать эту матрицу гораздо сложнее, нежели ее предшественницу, однако если настроить формулу один раз (что сводится к операциям умножения и сложения), вы сможете использовать ее во всех остальных преобразованиях. Вот они.

1. Преобразование по оси x

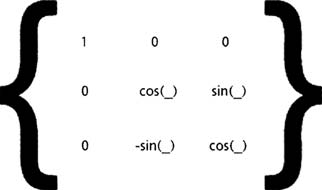
2. Преобразование по оси z

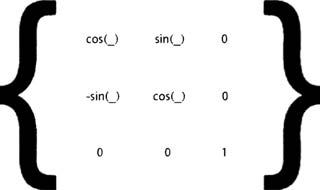
3. Изменение размера объекта

Эти матрицы легко представить в виде линейных массивов, однако в примере будет выбран способ, аналогичный тому, что мы делали при преобразовании градиентов. После создания матрицы мы вызываем функцию transform для добавления этой матрицы в полное преобразование.

Несмотря на то, что мы осуществляем три отдельных преобразования, они не будут применены к модели, пока не будет вызвана функция render, один раз в каждом кадре. Запустите фильм, чтобы увидеть результат работы.

С помощью матриц преобразования размером 3х3, вращение нашей каркасной модели вокруг всех трех осей осуществляется более эффективно.