3.2.2.2. Скрытое распределение Дирихле

Скрытое распределение Дирихле (LDA) относительно новый метод, был впервые представлен как метод информационного поиска в 2002 году. LDA – это статистический метод, который, используя баейсовские вероятности, определяет, насколько релевантен данный документ заданной теме. Как и описанные выше методы латентно-семантического анализа, LDA предполагает наличие латентных связей между словами и их контекстом, определяющим релевантность документа, анализируя встречаемость слов и словосочетаний в коллекции документов, метод предполагает, что наблюдаемые слова документа — результат влияния скрытых факторов (тем).

В теории вероятностей и математической статистике распределение Дирихле Dir(α) — это семейство непрерывных многомерных вероятностных распределений, параметризованных вектором α неотрицательных вещественных чисел. Его функция плотности вероятности возвращает доверительную вероятность того, что вероятность каждого из K взаимноисключающих событий равна x_i при условии, что каждое событие наблюдалось α_i − 1 раз:

Распределение Дирихле является сопряжённым априорным распределением к мультиномиальному распределению, а именно:

если X=(X₁,...,X_K) ~ Dir(α) и β|X=(β₁,...,β_K)|X~Mult(X) , то X|β ~ Dir(α+β)

где β_i — число вхождений i в выборку из n точек дискретного распределения на {1, …, K} определенного через X.

Эта связь используется в Байесовской статистике для того, чтобы оценить скрытые параметры дискретного вероятностного распределения X, имея набор из n выборок. Очевидно, если априорное распределение обозначено как Dir(α), то Dir(α+β) - апостериорное распределение после серии наблюдений с гистограммой β.

В модели LDA используются упрощения концепции «Bag of Words» и следующие положения:

• документы представляют собой совместное распределение скрытых тем,

• каждая тема — результат распределения слов словаря.

Пусть М — количество документов, К — количество тем, V — размер словаря, w_n — n-тое слово документа w. Процесс генерации каждого документа w может быть описан следующими шагами:

1. Выбор вектора распределения тем в документе, который описывается многомерной случайной величиной θ, имеющей распределение Дирихле θ~Dir(α)

2. Для каждого слова w_т

2.1. выбор скрытой темы z_n с помощью мультиномиального распределения z_n~Mult(θ_i)

2.2. Выбор слова w_n с помощью мультиномиального распределения w_n ~Mult(b, z_n)

Наблюдаемыми переменными при этом являются только w_n, остальные — скрытые. На рис. 3.1 модель LDA показана графически.

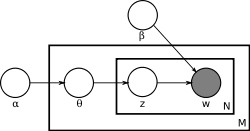
Рисунок 3.1. Графическое представление LDA-модели, имеющей 3 уровня: корпус текстов~ (α, b), документ ~(θ), слово ~ (z,w)

Вероятность совместного распределения:

Маргинальная вероятность для документа w:

Процедура классификации в LDA-модели традиционна в рамках статистических методов:

Однако ключевым моментом здесь является то, что в качестве оценки вероятности P(w|c_i) LDA-метод использует . В этом случае классификатор имеет вид:

Модель LDA, как правило, работают лучше на небольших наборах данных, поскольку байесовские методы не могут подстраиваться под изменение данных.