Лекция № 3. Автоматическое распознавание речи

1. Коммуникационный акт.

1.1. Структура коммуникационного акта.

В конце 40-х гг. американский математик Клод Шеннон [2] ввёл модель коммуникации (рис. 1).

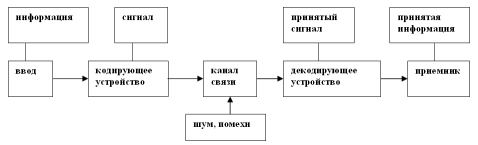
Рис. 7.1. Информационно-кодовая модель коммуникации Шеннона и Уивера

Механизм ее работы таков – сначала коммуникатор решает, какое из имеющихся сообщений ему активировать. После выделения оно модифицируется в сигнал с помощью какого-либо кодирующего устройства в сигнал, который идет через коммуникационный канал связи к декодирующему устройству, с помощью которого реципиент воспринимает данное сообщение и декодирует его. Например, для телефона канал - это провод, сигнал - электрический импульс, идущий по нему, а средства отправления и восприятия – микрофон и телефон. В разговоре же средством отправления являются артикуляторные органы, сигналом - колебание звуковых волн, проводящим каналом - воздух (разговор в вакууме невозможен) а ухо реципиента - средством восприятия. При рассмотрении схемы передачи сообщения необходимо учесть искажения, вносимые каналом передачи информации, которые обобщенно можно назвать шумом.

Процесс передачи включается в более общее действие, которое состоит из процессов трех уровней: технического, семантического и интенционального. Технические проблемы заключаются в том, как наиболее четко и аккуратно передать сообщение реципиенту. Семантический уровень определяет смысл сообщения. И, наконец, проблема интенционального уровня заключается в наиболее эффективном изменении поведения реципиента в направлении, указанном сообщением. В данном случае нас интересуют проблемы технического и семантического уровней.

Коммуникационный акт в наиболее простом случае может быть представлен как передача адресантом одного из известных адресату кодов с последующим выбором адресатом на основе полученного зашумленного кода наиболее вероятной гипотезы о переданном сообщении. Этот выбор называется классификацией – отнесением полученного сообщения к одному из классов. Аналитически обосновано, что не существует классификатора, работающего лучше Байесовского классификатора (классификатора, работающего на основе правила Байеса).

Используем методы статистического моделирования для интерпретации речевых событий, поступающих на вход системы.

На входе системы, использующей статистические методы моделирования, имеется последовательность векторов признаков , полученных в результате первичной обработки (например, речевой волны). Для выработки статистических гипотез берется некоторое множество классов , к которым эти гипотезы должны быть отнесены. В общем случае задача классификации может рассматриваться как статистическая задача распознавания образов, что позволяет построить оптимальный классификатор на основе критерия максимума апостериорной вероятности:

, (11)

где – вероятность принадлежности заданного образа классу .

1.2. Правило Байеса.

Пусть имеется группа событий (классов, к которым относятся входные сообщения), обладающая следую­щими свойствами:

1) все события попарно несовместны: ;

2) их объединение образует пространство элементарных исходов :

.

В этом случае будем говорить, что H₁, H₂,..., H_n образуют полную группу событий. Такие события иногда называют гипотезами.

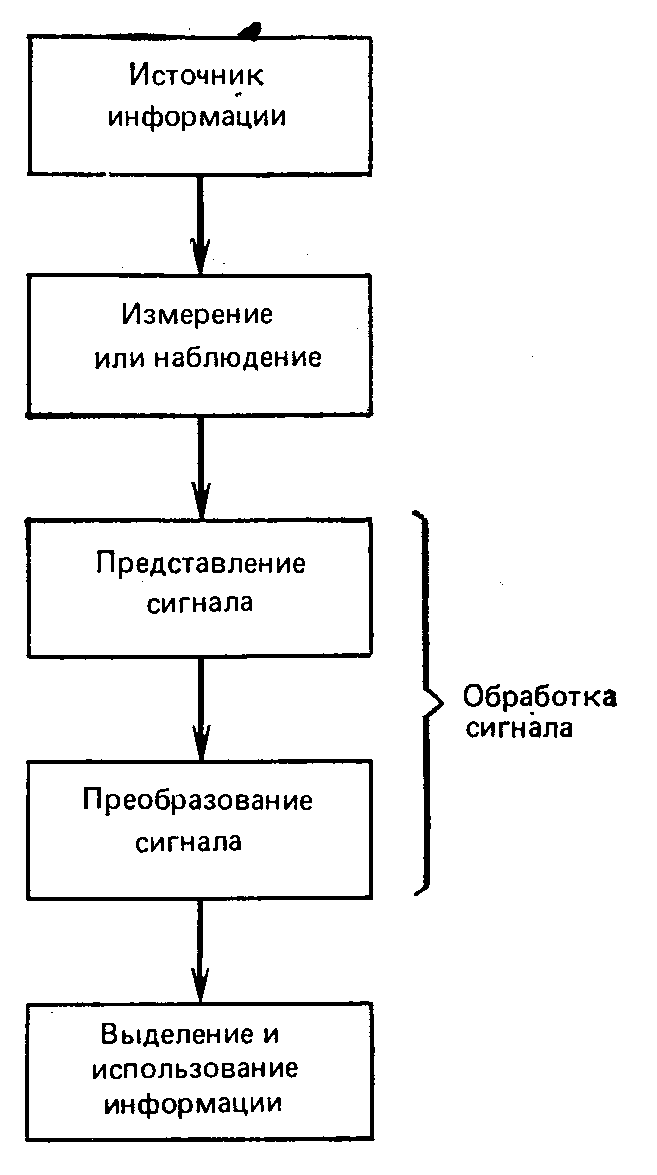
Рис. 7.2. Декодирование сигнала и выделение информации.

Пусть - полная группа событий и – некоторое событие. Тогда по формуле Байеса исчисляется вероятность реализации гипотезы при условии, что событие А произошло. Формула Байеса, полученная Т. Байесом в 1763 году, позволяет вычислить апостериорные вероятности событий через априорные вероятности и функции правдоподобия.

Здесь А – конкретное наблюдение (измерение). Формулу Байеса еще называют формулой вероятности гипотез. Будем считать, что у нас достаточно данных для определения вероятности принадлежности объекта каждому из классов. Вероятность называют априорной вероятностью гипотезы , а вероятность – апостериорной вероятностью, поскольку задает распределение индекса класса после эксперимента (a posteriori – т.е. после того, как измерение было произведено). Также будем считать, что известны функции распределения вектора признаков для каждого класса . Они называются функциями правдоподобия A по отношению к H_k. Если априорные вероятности и функции правдоподобия неизвестны, то их можно оценить методами математической статистики на множестве прецедентов. Байесовский подход исходит из статистической природы наблюдений. За основу берется предположение о существовании вероятностной меры на пространстве образов, которая либо известна, либо может быть оценена. Цель состоит в разработке такого классификатора, который будет правильно определять наиболее вероятный класс для пробного образа. Тогда задача состоит в определении "наиболее вероятного" класса.

Если априорные вероятности и функции правдоподобия неизвестны, то их можно оценить методами математической статистики на множестве прецедентов. Например, , где – число прецедентов из . N – общее число прецедентов. может быть приближено гистограммой распределения вектора признаков для прецедентов из класса .

Рассмотрим случай двух классов и . Естественно выбрать решающее правило таким образом: объект относим к тому классу, для которого апостериорная вероятность выше. Такое правило классификации по максимуму апостериорной вероятности называется Байесовским: если , то А классифицируется в , иначе в . Таким образом, для Байесовского решающего правила необходимо получить апостериорные вероятности . Это можно сделать с помощью формулы Байеса.

Итак, Байесовский подход к статистическим задачам основывается на предположении о существовании некоторого распределения вероятностей для каждого параметра. Недостатком этого метода является необходимость постулирования как существования априорного распределения для неизвестного параметра, так и знание его формы.