2.15 Вычисление массы кривой с помощью определенного интеграла

Предположим, что кусок проволоки описывается некоторой пространственной кривой C. Пусть масса распределена вдоль этой кривой с плотностью ρ (x,y,z). Тогда общая масса кривой выражается через криволинейный интеграл первого рода

Если кривая C задана в параметрическом виде с помощью векторной функции  , то ее масса описывается формулой

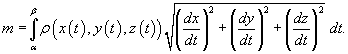
В случае плоской кривой, заданной в плоскости Oxy, масса определяется как

или в параметрической форме

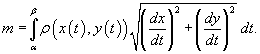
2.16 понятие момента фиксированного порядка n>1, n=1 и соответствующегося ему центра у массы вдоль кривой.

Центр масс и моменты инерции кривой

Пусть снова кусок проволоки описывается некоторой кривой C, а распределение массы вдоль кривой задано непрерывной функцией плотности ρ (x,y,z). Тогда координаты центра масс кривой определяются формулами

где

− так называемые моменты первого порядка.  Моменты инерции относительно осей Ox, Oy и Oz определяются формулами

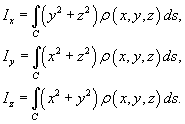
3.Вопросы потеме «кратные интыгралы»

3.2 Свойство аддитивности кратного интеграла

• Аддитивность по множеству интегрирования. Пусть множества G₁ и G₂ измеримы, 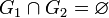  и 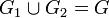 . Пусть также функция f определена и интегрируема на каждом из множеств G₁ и G₂. Тогда интеграл по G существует и равен

.

.3.3. свойство линейности для кратного интеграла

Линейность по функции. Пусть   измеримо, функции   и   интегрируемы на  , тогда

.

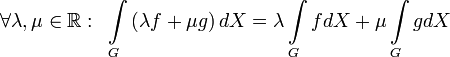3.4.Сведенья кратного интеграла к интегралам одной переменной.

Кратным (n-кратным) интегралом функции   на множестве   называется число   (если оно существует), такое что, какой бы малой  -окрестностью числа   мы ни задались, всегда найдется такое разбиение множества   и набор промежуточных точек, что сумма произведений значения функции в промежуточной точке разбиения на меру разбиения будет попадать в эту окрестность. Формально:

 :   : 

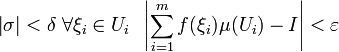
Здесь   — мера множества  .

Это определение можно сформулировать в другой форме с использованием интегральных сумм. А именно, для данного разбиения   и множества точек   рассмотрим интегральную сумму

Кратным интегралом функции   называют предел

если он существует. Предел берётся по множеству всех последовательностей разбиений, с мелкостью стремящейся к 0. Разумеется, это определение отличается от предыдущего, по сути, лишь используемым языком.

Интеграл обозначается следующим образом:

• В векторном виде:  ,

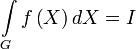• Либо ставят значок интеграла 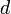  раз, записывают функцию и   дифференциалов:  .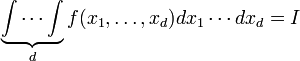

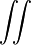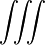• Для двойного и тройного интегралов используются также обозначения   и   соответственно.

В современных математических и физических статьях многократное использование знака интеграла не применяется.

Такой кратный интеграл называется интегралом в собственном смысле.

4.1 два типа криволинейногоинтеграла

Криволинейный интеграл первого типа (по длине дуги)

Пусть в некоторой области D плоскости хоу (см. рис. 1) задана непрерывная функция f(x, y) и гладкая незамкнутая кривая L между точками А, В.

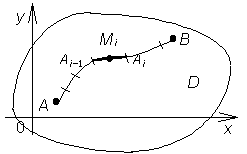Рис. 1

Составим интегральную сумму по уже известному алгоритму. Разобьём кривую L точками

А = А₀, А₁, ..., А_п = В

на п произвольных участков l_i, обозначив через   длину i-го участка кривой между точками А_i-1, A_i, где I = 1, 2, …,п.

В каждом i-том участке выберем произвольно точку   и подсчитаем в ней значение функции f_i = f(M_i).

Просуммировав произведения  по всем i = 1, 2, …, п, получим интегральную сумму

.

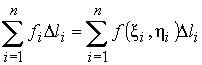Предел этой интегральной суммы, если он существует и не зависит от типа разбиения дуги L и способа нахождения точек M_i, где i = 1, 2, …, п, называется криволинейным интегралом первого типа от функции f(x, y), взятым по кривой L, и обозначается

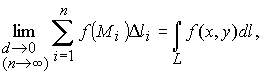
где  .

Этому интегралу можно придать вполне определённый физический смысл: если в каждой точке дуги L задана переменная плотность   - функция точки, то можно подсчитать массу материальной дуги АВ:

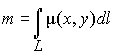. (1)

Сравните с задачей о вычислении массы неоднородного стержня, приводящей к понятию определённого интеграла .