2.11 Вычисление площади фигуры с помощью определенного интеграла
Определение. Разность
F (b)– F (a) называется интегралом от функции
f (x) на отрезке [ a ; b ] и обозначается
так: 
=
F (b)– F (a) –
формула Ньютона-Лейбница.
Геометрический смысл интеграла.
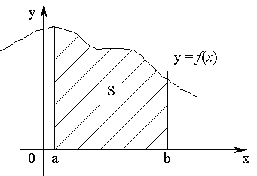
Площадь криволинейной трапеции, ограниченной графиком непрерывной положительной на промежутке [ a ; b ] функции f (x), осью Ох и прямыми х=а и х= b:
.
Вычисление площадей с помощью интеграла.
1.Площадь фигуры, ограниченной графиком непрерывной отрицательной на промежутке [ a ; b ] функции f (x), осью Ох и прямыми х=а и х= b :
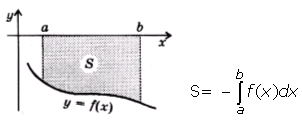
2.Площадь
фигуры, ограниченной графиками непрерывных
функций f (x), 
и
прямыми х=а, х= b :
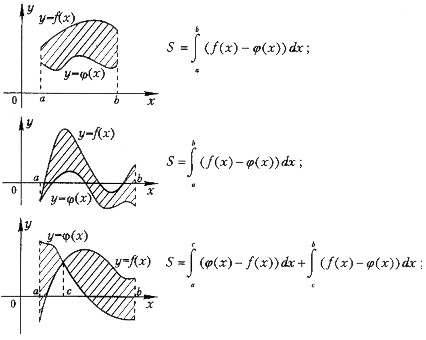
3.Площадь фигуры, ограниченной графиками непрерывных функций f (x) и :
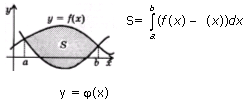
4.Площадь фигуры, ограниченной графиками непрерывных функций f (x), и осью Ох:
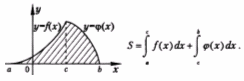
2.12 Вычисление длины кривой, в том числе пространственной, с помощью определенного интеграла
Определение длины дуги.
Пусть на плоскости задана некоторая кривая АВ. Прежде всего надо описать ее математически. Самым общим заданием плоской кривой считается ее параметрическое задание, когда кривая задается системой
.
Разобьем
отрезок 
на
части
,
и
пусть 
.
Тогда вся кривая АВ разобьется
на кусочки точками Мi, 
(см.
рис. 5.4).
Рис. 5.4 К определению длины дуги плоской кривой
Соединим
точки 
отрезками
прямых, и пусть li есть
длина отрезка прямой, соединяющей
точки Mi и Mi+1.
Найдем периметр вписанной ломаной
.
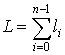Если
существует 
и
этот предел не зависит от способа
разбиения отрезка
на
кусочки, то он называется длиной
дуги кривойАВ.
Вычисление длины дуги.
Теорема. Пусть
функции x(t)
и y(t)
имеют на отрезке
непрерывные
производные 
и 
.
Тогда длина дуги кривой
.
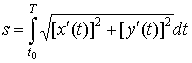Частные случаи.
1. Явное
задание кривой.
В этом случае кривая задается в
виде 
, 
, и
длина ее дуги равна
.
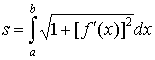2. Кривая
в полярных координатах. Уравнение
кривой имеет в этом случае вид 
и
длина ее дуги равна
.
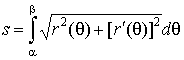Длина дуги пространственной кривой.
В
трехмерном пространстве кривая задается
в виде 
и
длина ее дуги равна
.
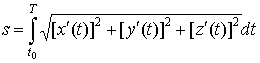Площади криволинейных трапеции и сектора
Криволинейной трапецией называется фигура, изображенная на рис. 5.5.
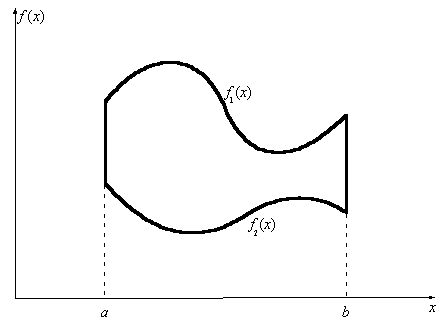
Рис. 5.5 Криволинейная трапеция
Ее площадь равна
.
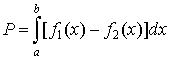Криволинейным сектором называется фигура, изображенная на рис. 5.6.
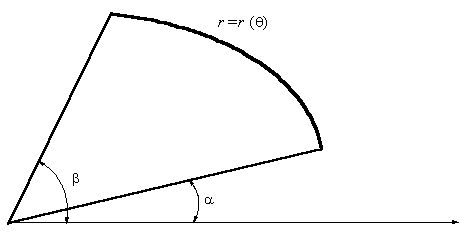
Рис. 5.6 Криволинейный сектор
Его площадь равна
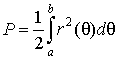
2.13 Вычисление площади поверхности тела вращения с помощью определенного интеграла
Площадь
поверхности вращения, образующейся при
вращении вокруг оси Ox дифференцируемой
кривой, определяется по формулам (в
зависимости от способа задания
кривой)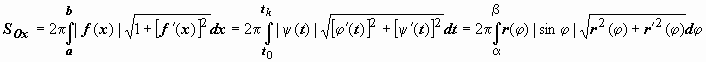 
(
-
длина окружности кольца, 
-
его ширина).
Пример:
найти площадь тора, образующегося при
вращении окружности 
вокруг
оси Ox.
Решение: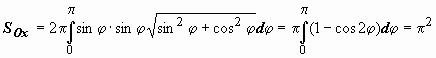 
.
2.14Объем и поверхность тела вращения.
Пусть на плоскости дана кривая, заданная параметрически
,
и это кривая вращается вокруг оси ОХ. Получающееся тело носит название тела вращения. Оно напоминает бочку (см. рис. 5.7).
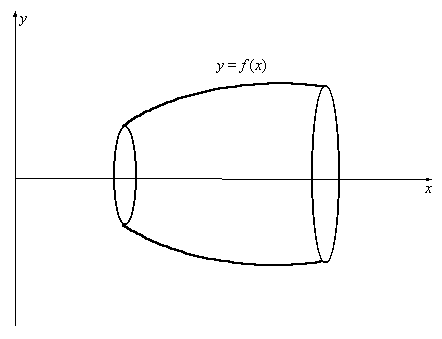
Рис. 5.7 Тело вращения
Его объем равен
,
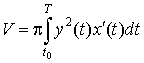а боковая поверхность равна
.
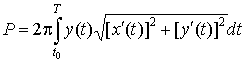Если
кривая задана явно 
,
то соответствующие выражения принимают
вид
, 
.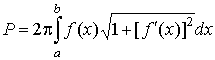