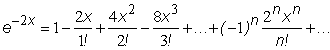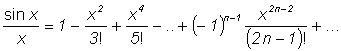7.1 Теорема существования радиуса сходимости у степенного ряда

Из теоремы Абеля следует, что существует такое число R   (возможно,  ) такое, что при   степенной ряд сходится, при   ряд расходится. Действительно, пусть в точке   ряд сходится, в точке  ряд расходится. Рассмотрим точку  , расположенную между областями, в которых установлена сходимость и расходимость. В точке   числовой ряд   либо сходится, либо расходится. Если он сходится, то мы можем перенести точку   в точку  ; если ряд в точке   расходится, мы переносим в   точку  . Продолжая этот процесс, мы сблизим точки   и  , эта граница и определит числоR.

Определение. Число R   такое, что при   степенной ряд сходится, при   ряд расходится, называется радиусом сходимости. Интервал   называется интервалом сходимостистепенного ряда.

Сходимость ряда в концевых точках интервала сходимости должна исследоваться отдельно. В зависимости от поведения ряда на концах интервала сходимости область сходимости степенного ряда может быть одной из следующих: ,  ,  ,  .

Итак, для определения области сходимости степенного ряда надо найти его интервал сходимости R, затем исследовать поведения ряда в концевых точках интервала сходимости  .

Примеры. 1.  . Для определения радиуса сходимости этого ряда целесообразно применить признак сходимости Дирихле. Однако этот признак, как и многие другие, может применяться только к положительному ряду, поэтому выпишем ряд, состоящий из абсолютных величин членов исследуемого ряда:. Применяем признак Дирихле: . Следовательно,  . Мы нашли радиус сходимости R =3 и интервал сходимости  . Исследуем поведение ряда на концах интервала: , ряд сходится. , ряд сходится абсолютно. Область сходимости - интервал [-7,7].

7.2 Формулы определения радиуса сходимости

Приведем способ определения радиуса сходимости степенного ряда

Теорема 2. Если существует предел то радиус сходимости ряда равен

Рассмотрим ряд . По условию существует . Обозначим его через Тогда

При каждом значении х степенной ряд становится числовым рядом.

Поэтому по признаку Даламбера ряд сходится если . т.е. .

Следовательно, по теореме о сходимости знакопеременных рядов ряд также сходится при причем абсолютно. При ряд расходится, так как и, следовательно, общий член ряда a_nxⁿ не стремится к нулю при .

Таким образом, данный ряд сходится внутри интервала и расходится вне его. т.е. радиус сходимости равен

Можно доказать, что если , то ряд сходится на всей числовой прямой т.е. а если , то ряд сходится только при x=0.т.е., R=0.

Пример 1. Рассмотрим ряд .Здесь и

Поэтому

Следовательно, по теореме 3 данный ряд сходится на интервале . Исследуем поведение ряда на концах интервала сходимости, т.е. в точках. При х=1 получаем гармонический ряд при ряд который сходится в силу признака Лейбница. Таким образом, данный ряд сходится в любой точке полуинтервала (-1. 1) и расходится вне его.

Пример 2. Ряд расходится на всей числовой прямой, кроме точки , так как его радиус сходимости

Пример 3. Ряд сходится абсолютно на всей числовой прямой так как его радиус сходимости .

Теорема 4. Если функция имеет производные до n+1 порядка в некоторой окрестности точки x=a, то, как известно из дифференциального исчисления, в каждой точке х этой окрестности она представима следующей формулой Тейлора:

f(x)=f(a)+(x-a)+ ++Rn(x), (2)

Rn(x)=.(0<0<1).

Остаточный член формулы Тейлора, записанный в форме Лагранжа. Пусть теперь функция f(x) некоторой окрестности точки х=a имеет производные всех порядков. Если для каждой точки х этой окрестности =0, то переход к пределу в формуле (2) при дает нам представление функции f(x) в виде бесконечного ряда:

f(x)=f(a)+(x-a)+… ++… (3)

Заметим, что независимо от того, выполняется условие или нет, ряд, стоящий в правой части равенства (3), называется рядом Тейлора для функции f(x).Если , то между рядом Тейлора для функции f(x), если только в точке х=а она имеет производные всех порядков, но этот ряд может и не иметь своей суммой функцию f(x).Функция f(x) называется разложимой в ряд Тейлора в окрестности точки х=а, если для нее справедливо равенство (3).Условием разложимости функции f(x) в ряд Тейлора является равенством .

Учитывая ранее изложенное, мы можем сделать следующее заключение: Чтобы разложить функцию f(x) в ряд Тейлора, нужно: 1) формально составить для нее ряд Тейлора, 2) найти область сходимости этого ряда, 3) выяснить, для каких х из области сходимости имеет место равенство .Для этих х и будет верна формула(8). Теорема 5. Для того чтобы ряд Тейлора(3) функции сходился к точке x, необходимои достаточно, чтобы в этой точке остаточный член формулы Тейлора стремился к нулю при , т.е. чтобы .

Пусть ряд Тейлора сходится к функции в некоторой окрестности точки x0 т.е. . Так как n-я частичная суммаряда() совпадает с многочленом Тейлора Pn(x), т.е. = Pn(x), находим: = === =0. Обратно, пусть . Тогда =

Замечание. Если ряд Тейлора (2) сходится к порождающей функции f(x), то остаточный член формулы Тейлора равен остатку ряда Тейлора, т.e. Rn(x)=rn(x). (Напомним, что Rn(x)=, а rn(x)=S(x) - - Sn(x), где S(x) - сумма ряда Тейлора). Таким образом, задача разложения функции f(x) в степенной ряд сведена к определению значений х, при которых Rn(x)0 (при ). Если сделать замену, то следует каким-нибудь иным способом убедиться, что написанный ряд Тейлора сходится к данной функции.

На практике часто пользуются следующей теоремой, которая дает простое достаточное условие разложимости функции в ряд Тейлора.

Теорема 6. Если модули всех производных функций f(x) ограничены в окрестности точки х0 одним и тем же числом М>0, то для любого х из этой окрестности ряд Тейлора функции f(x), т.е. имеет место разложение:

f(x)=f(a)+(x-a)+…=. (8)

Согласно теореме(3) достаточно показать, что . По условию теоремы (6) для любого n имеет место неравенство.Тогда имеем:

Осталось показать, чтоДля этого рассмотри ряд

Так както по признаку Даламбера этот ряд сходится на всей числовой оси. Но тогда, в силу необходимого признака сходимости

Следовательно, .

Теорема 7. Степенной ряд можно почленно дифференцировать в каждой точке х его интервала сходимости - R<x<R, то есть из справедливости равенства (А) Следует справедливость (Б)

При этом интервал сходимости ряда (Б) совпадает с интервалом сходимости ряда (А).

Фиксируем произвольную точку х интервала сходимости (-R, R) данного ряда и докажем, что в этой точке степенной ряд можно почленно дифференцировать. С этой целью построим отрезок [-p, p], содержащейся в интервале (-R, R) содержащей точку х. Покажем, что на этом отрезке ряд производных от членов данного ряда сходится равномерно. Докажем теперь, что функция е^x - сумма Возьмем точку хn удовлетворяющую условию Q<x0<0. Учитывая, что ряд сходится, что, и следовательно, его члены при всех n ограничены по модулю , также, принимая во внимание неравенство , оценим общий член ряда производных по модулю: (11). Отметим, что в силу необходимого условия сходимости Замечая, что числовой ряд с общим членом сходится (действительно, по признаку Даламбера , мажорирует ряд с общим членом на отрезке [-p, p] на основании признака Вейерштрасса, заключаем, что ряд сходится равномерно на отрезке [-p, p]. Так как члены этого ряды непрерывны на том же отрезке, то отсюда, на основании теоремы о дифференцировании функциональных рядов, вытекает, что данный степенной ряд можно почленно дифференцировать в каждой точке отрезка [-p, p], в том числе и в упомянутой точке х.

Итак, равенство (Б) доказано для всякой точки х интервала сходимости - R<x<R данного ряда. Отсюда следует, что радиус сходимости ряда производных (Б) не меньше R. Докажем, что он не может быть и больше R. С этой целью предположим противное, то есть что ряд (Б) сходится в интервале , где . Тогда, проинтегрировав равенство (Б) на отрезке [0, x], мы получим исходное равенство (А), которое в силу теоремы об интегрировании степенных рядов должно иметь место в интервале более широком, чем (-R, R). Так как это невозможно, то заключаем, что Теорема доказана.

Следствие. Степенной ряд можно почленно дифференцировать в каждой точке х его интервала сходимости сколько угодно раз.

Действительно, ряд , полученный почленным дифференцированием данного ряда, является степенным и поэтому к нему приложима доказанная теорема, на основании которой его снова можно дифференцировать. Так как и дальнейшие дифференцирования приводят к степенным рядам, то справедливость следствия очевидна.

Заметим, что m-кратное дифференцирование степенного ряда приводит к формуле

При этом интервалы сходимости всех производных рядов совпадают с интервалом сходимости исходного ряда.

7.7 Если функция  y = f(x)  имеет производные в окрестности точки x = x₀   до (n+1) - го порядка включительно, то существует точка      , такая, что  

(1)

где        

Формула (1) называется формулой Тейлора функции y = f(x)  для точки x₀,

R_n (x) - остаточным членом формулы Тейлора в форме Лагранжа. 

Многочлен 

называется многочленом Тейлора функции y = f(x).

При x₀ = 0  приходим к частному случаю формулы (1): 

(2)

где 

Формула (2) называется формулой Маклорена функции   y = f(x). 

Сформулируем условие разложимости функции в ряд Тейлора.

Если функция  f(x)  дифференцируема в окрестности точки x₀ любое число раз и в некоторой окрестности этой точки      , то 

(3)

 При x₀ = 0  

(4)

Ряд (3) называется рядом Тейлора, а ряд (4) – рядом Маклорена.

Приведем разложения в степенные ряды некоторых функций:

	(5)
	(6)
	(7)
	(8)
(-1 < x < 1)	(9)

Для каждого случая в скобках указана область, в которой степенной ряд сходится к соответствующей функции. 

Последний ряд, называемый биномиальным, на концах интервала сходимости ведет себя по - разному в зависимости от  ; при   абсолютно сходится в   ; при   -1 < m < 0расходится в точке x = -1 и условно сходится в точке x = 1 при   расходится в точках  . 

В общем случае разложение в степенные ряды основано на использовании рядов Тейлора или Маклорена. Но на практике степенные ряды многих функций можно найти формально, используя ряды (5 - 9).

Например, при разложении в степенной ряд функции   в формулу (6) вместо подставляем   . Тогда:   

Полученный ряд сходится при любых   , но следует помнить, что функция   не определена при x < 0 . Поэтому найденный ряд сходится к функции только в полуинтервале   .

Аналогично можно записать степенные ряды функций  f (x) = e^-2x   и   .