5.6Примеры числовых, функциональных и оперативных рядов Числовые ряды

Пусть задана бесконечная последовательность чисел  . Выражение

                                                                                                                   (97)

называется числовым рядом. Числа   называются членами этого ряда. Член   ряда (97), стоящий на  -м месте, считая от начала, называется общим членом этого ряда. Ряд (97) считается заданным, если известен общий член его, выраженный как функция номера  .

Выражение (97) удобно обозначать следующим образом: .

Сумма конечного числа n первых членов ряда называетсяn-ой частичной суммой ряда.

Рассмотрим частичные суммы:        

Если существует конечный предел  , то его называют суммой ряда (97) и говорят, что ряд (97) сходится.

Если   не существует (например  , при  ), то говорят, что ряд (97) расходится и суммы не имеет.

Пример 7.1.1. Определить сходимость числового ряда

                                                     .                                                (98)

Решение. Данный числовой ряд – сумма всех членов геометрической прогрессии с первым членом   и знаменателем     Вычисляя сумму первых   чисел, получаем:

 или  .

Переходя к вычислению предела, заметим, что в зависимости от значений   и   частичная сумма ряда принимает различные значения.

1). Если  , то   при  . Значит, в случае  ряд (98) сходится и его сумма  .

2). Если  , то   и тогда   при  , т.е.   не существует. Таким образом, в случае   ряд (98) расходится.

3) Если  , то ряд (98) имеет вид:  . В этом случае  , т.е. ряд расходится.

Если   то  . В этом случае: 

Следовательно, частичная сумма предела не имеет.

Таким образом, сумма членов геометрической прогрессии (с первым членом отличным от нуля) сходится только тогда, когда знаменатель прогрессии по абсолютной величине меньше единицы. ►

Теорема. Если сходится ряд, получившийся из данного ряда (97) отбрасыванием нескольких его членов, то сходится и сам данный ряд. Обратно, если сходится данный ряд, то сходится и ряд, получившийся из данного отбрасыванием нескольких членов.

Теорема. Если ряд (97) сходится и его сумма равная S, то ряд

                                                                                                      (99)

где   – произвольное действительное число, так же сходится и его сумма равна .

Теорема.

                                                ,                                                         (100)

                                                                                                           (101)

сходятся и их суммы, соответственно равны   и  , то ряды

                                              ,                                                    (102)

                                                                                                   (103)

также сходятся и их суммы равные соответственно   и  .

Теорема. (Необходимый признак сходимости ряда). Если ряд сходится, то его n-й член стремится к нулю при неограниченном возрастании n.

Следствие. Если n-й член ряда не стремится к нулю, то ряд расходится.

Пример 7.1.2. Определить сходимость числового ряда  .

Решение. Воспользуемся необходимым признаком сходимости ряда. Для данного числового ряда записываем формулу общего члена и вычисляем предел

.

Так как предел не равен нулю, то исходный ряд расходится. ►

Подчеркнем, что рассмотренный признак является только необходимым, но не является достаточным, то есть из того, что n-й член ряда стремится к нулю, ещё не следует, что ряд сходится – ряд может и расходиться.

Пример 7.1.3. Определить сходимость числового ряда

                                                     .                                                       (104)

Решение. Для данного числового ряда записываем формулу общего члена и вычисляем предел  . Необходимый признак выполнен. Докажем, однако, что исходный ряд расходится. Распишем его подробнее:

                                   (105)

и составим вспомогательный ряд:

               .                                   (106)

Ряд (106) строится следующим образом: его первый член равен 1, второй –  , третий и четвёртый равны  , члены с пятого по восьмой равны  , члены с девятого по 16-й равны  , с 17-го по 32-й –  , и т.д.

Обозначим через Sn⁽¹⁾ сумму первых n членов гармонического ряда (105), а через Sn⁽²⁾ сумму первых n членов ряда (106). Так как каждый член ряда (105) больше соответствующего члена ряда (106), то для (n > 2) выполнено

                                                          .                                                                 (107)

Подсчитаем частичные суммы ряда (106) для значений n равных степеням двойки: 2¹, 2², 2³, 2⁴, 2⁵ и т.д. Имеем:

,

,

,

,

Заметим, что  ,  , и т.д. Следовательно  , т.е. частичные суммы Sn⁽²⁾ при   неограниченно увеличиваются или  . Но тогда из соотношения (107) следует, что  . Таким образом, исходный числовой ряд расходится. Числовой ряд (104) часто называютгармоническим. ►

Пусть даны два ряда с положительными членами

                                                     ,                                                        (108)

                                                     .                                                         (109)

Для них справедливы следующие утверждения.

Теорема (Первый признак сравнения числовых рядов). Пусть члены ряда (108) не больше соответствующих членов ряда (109), т.е. при n=1, 2, ...

                                                               .                                                                   (110)

Тогда, если ряд (109) сходится, то сходится и ряд (108).

Теорема (Второй признак сравнения числовых рядов). Пусть члены ряда (108) не меньше соответствующих членов ряда (109), т.е. при n=1, 2, ...

                                                               .                                                                  (111)

Тогда, если ряд (109) расходится, то расходится и ряд (108).

Пример 7.1.5. Определить сходимость числового ряда  .

Решение. Поскольку все слагаемые данного числового ряда положительны, воспользуемся вторым признаком сравнения. Так как  , то члены данного ряда больше соответствующих членов гармонического ряда  , который расходится (см. пример 7.1.3). Поэтому исходный числовой ряд также расходится. ►

Теорема (Признак сходимости Даламбера).Пусть дан числовой ряд (97) с положительными членами. Если отношение (n+1)-го члена к n-му члену при   имеет конечный предел, т.е.

                                                          ,                                                               (112)

то       1) при  <1 – ряд сходится;

  2) при  >1 – ряд расходится.

Замечание. Ряд будет расходиться и в том случае, когда  . Это следует из того, что если  , то, начиная с некоторого номера n=N, будет иметь место неравенство:  >1. Следовательно,  > .

Пример 7.1.6. Исследовать сходимость ряда 

Решение. Воспользуемся признаком сходимости Даламбера. Определим формулу общего члена числового ряда и составим отношение  ,  ,  . Вычисляя предел, получим

<1.

Таким образом, исходный ряд сходится. ►

Пример 7.1.7. Исследовать сходимость ряда  .

Решение. Воспользуемся признаком сходимости Даламбера. Определим формулу общего члена числового ряда и составим отношение  ,  ,  . Вычисляя предел, получим

 > 1.

Таким образом, исходный ряд расходится. ►

Признак Даламбера дает ответ на вопрос о том сходится ли данный положительный ряд в случае, когда   существует и отличен от 1. Если же этот предел не существует или  , то признак Даламбера не дает возможности установить, сходится ряд или расходится, так как в этом случае ряд может оказаться или сходящимся, или расходящимся. Для решения вопроса о сходимости надо применить какой-либо другой признак.

Если  , но отношение   для всех номеров n, начиная с некоторого больше 1, то ряд расходится. Это следует из того, что если  >1, то   >   и общий член ряда не стремится к 0 при n®¥.

Теорема (Признак Коши). Если для ряда с положительными членами (97) величина   имеет конечный предел   при  , т.е.

,

то       1) при  < 1 – ряд сходится;

           2) при  > 1 – ряд расходится.

Замечание. Как и в признаке Даламбера, случай  , требует дополнительного исследования. Среди рядов, удовлетворяющих этому условию, могут встретиться как сходящиеся, так и расходящиеся. Так для гармонического ряда имеем:  , но он расходится. Рассмотрим другой числовой ряд  . Для него так же имеет место равенство  , но он сходится по первому признаку сходимости. Заметим, что если отбросить первый член, то члены оставшегося ряда будут меньше соответствующих членов ряда  , который сходится (см. пример 7.1.10).

Пример 7.1.11. Исследовать сходимость ряда 

Решение. Воспользуемся признаком сходимости Коши. Определим формулу общего члена числового ряда и вычислим предел  .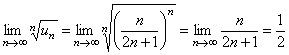

Так как предел конечен и меньше единицы, то по признаку Коши исходный числовой ряд сходится. ►

Приведем без доказательства признак сходимости числовых рядов с положительными членами, который удобно использовать, когда признаки Даламбера и Коши не дают ответа на вопрос о сходимости ряда.

Теорема (Интегральный признак сходимости).Пусть дан ряд  , члены которого положительны и не возрастают, т.е.  , а функция  , определена  при  , непрерывная и не возрастающая и  . Тогда для сходимости ряда   необходимо и достаточно, чтобы сходился несобственный интеграл  .

Пример 7.1.12. Исследовать сходимость обобщенного гармонического ряда  .

Решение. Пусть  . Функция   при   (а значит и при  ) положительна и невозрастающая (точнее убывающая). Поэтому сходимость ряда равносильна сходимости несобственного интеграла  . Имеем  .

Если  , то  .

Если  , то 

Итак, данный обобщенный гармонический ряд сходится при   и расходится при  . ►

Знакочередующимся рядом называется ряд

                                            ,                                                       (113)

где  , – положительные числа.

Теорема (Признак Лейбница). Если в знакочередующемся ряде (113) члены таковы, что

                                                                                                                       (114)

и

                                                                                                                              (115)

то ряд (113) сходится, его сумма положительна и не превосходит первого члена.

Замечание. Теорема Лейбница справедлива, если неравенства (114) выполняются, начиная с некоторого номера N.

Теорема Лейбница иллюстрируется геометрически следующим образом. На числовой прямой будем откладывать (рис. 21)частичные суммы:

,  ,  ,  , …

Рис. 21. Геометрический смысл теоремы Лейбница

Тогда точки, соответствующие частичным суммам будут приближаться к некоторой точке S. При этом точки, соответствующие чётным суммам располагаются слева от S, а нечетным суммам – справа от S.