
- •1.Вопросы по теме «общее представление об интеграле»
- •1.3 Определение меры
- •1.4 Дифференциал как мера
- •1.5 Интегрирование по мере
- •2Вопросы по теме « интегралы одной переменной»
- •2.1 Определение неопределенного интеграла
- •2.2 Свойство линейности для неопределенного интеграла
- •2.3 Метод интегрирования заменой переменой
- •Получение формул [править]Для неопределённого интеграла
- •[Править]для определённого интеграла
- •2.5 Интегрирование рациональных дробей Интегрирование рациональных дробей
- •2.6 Основная серия подходов для интегрировая тригонометрических выражений
- •2.8. Геометрический смысл определенного интеграла на произвольном измеримом множестве числовой прямой
- •2.9Сведение определенного интеграла к неопределенному
- •2.10 Основные типы несобственных интегралов и правил работы с ними Несобственный интеграл с бесконечным пределом (ами) интегрирования
- •Несобственный интеграл с бесконечным пределом (ами) интегрирования
- •2.11 Вычисление площади фигуры с помощью определенного интеграла
- •2.12 Вычисление длины кривой, в том числе пространственной, с помощью определенного интеграла
- •2.13 Вычисление площади поверхности тела вращения с помощью определенного интеграла
- •2.15 Вычисление массы кривой с помощью определенного интеграла
- •3.Вопросы потеме «кратные интыгралы»
- •3.2 Свойство аддитивности кратного интеграла
- •3.4.Сведенья кратного интеграла к интегралам одной переменной.
- •Криволинейный интеграл первого типа (по длине дуги)
- •Криволинейный интеграл второго типа (по координатам)
- •4.3 Критерий независимости криволинейного интеграла второго типа от пути
- •1Плоский случай
- •2Пространственный случай
- •4.4 Нахождение функции по ее полному дифференциалу
- •4.5 Типы поверхностного интеграла
- •1. Поверхностные интегралы первого типа
- •4.6 Теореме дифференцирования интеграла по параметру
- •5.Вопросы по теме « общее положение о рядах»
- •5.1 Общее определение ряда
- •5.2 Определение суммы ряда.Необходимый признак сходимости ряда Определение
- •5.3Абсолютная и простая сходимлсть рядов.
- •5.6Примеры числовых, функциональных и оперативных рядов Числовые ряды
- •Функциональные ряды
- •7.1 Теорема существования радиуса сходимости у степенного ряда
- •7.2 Формулы определения радиуса сходимости
- •7.9. Ряды тейлора и маклорена для функций нескольких переменных Формула Тейлора для функции нескольких переменных
4.6 Теореме дифференцирования интеграла по параметру
Дифференцирование по параметру
Если
функция ![]() и
ее частная производная
и
ее частная производная ![]()
![]() непрерывны
на множестве
непрерывны
на множестве ![]()
![]()
![]() ,
а функции
,
а функции ![]() и
и ![]() дифференцируемы
на интервале
дифференцируемы
на интервале ![]()
![]() и
удовлетворяют на нем условиям
и
удовлетворяют на нем условиям ![]()
![]()
![]() ,
то при
,
то при
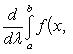
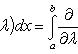
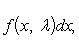
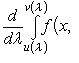
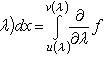
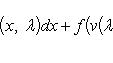
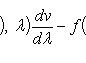
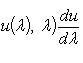 (правило
Лейбница).
(правило
Лейбница).
Первая
формула остается в силе и для несобственных
интегралов, если предположить, что
интеграл ![]()
![]() сходится,
а интеграл
сходится,
а интеграл 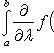
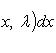 равномерно
сходится на интервале
.
(При этом функция
и
ее производная
предполагаются
непрерывными лишь на множестве
равномерно
сходится на интервале
.
(При этом функция
и
ее производная
предполагаются
непрерывными лишь на множестве ![]()
![]()
![]() или
на множестве
или
на множестве ![]()
![]()
![]() .)
.)
Второй случай часто можно свести к первому подходящей заменой переменных. Отметим также, что
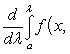
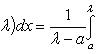
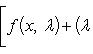
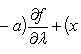
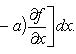
5.Вопросы по теме « общее положение о рядах»
5.1 Общее определение ряда
ОПРЕДЕЛЕНИЕ.
Пара числовых последовательностей
{ an }
и { Sn }
, где 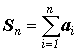 называется
(числовым) рядом (илибесконечной
суммой)
и обозначается
называется
(числовым) рядом (илибесконечной
суммой)
и обозначается ![]() .
Элементы последовательности { an }
называют членами
ряда,
а элементы последовательности { Sn }
– частичными
суммами ряда.
.
Элементы последовательности { an }
называют членами
ряда,
а элементы последовательности { Sn }
– частичными
суммами ряда.
ОПРЕДЕЛЕНИЕ.
Если существует конечный предел
последовательности { Sn }
, который мы обозначим S,
тогда S называютсуммой
ряда;
а сам ряд именуют сходящимся и
пишут : 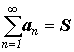 .
Если же последовательность { Sn }
не имеет конечного предела, ряд
именуют расходящимся.
.
Если же последовательность { Sn }
не имеет конечного предела, ряд
именуют расходящимся.
Для задания ряда достаточно задать только одну из последовательностей { an } или { Sn }. Сходимость ряда эквивалентна сходимости последовательности { Sn } , и поэтому исследование ряда можно свести к исследованию последовательности {Sn }.
5.2 Определение суммы ряда.Необходимый признак сходимости ряда Определение
Пусть ![]() — числовой
ряд.
Число
— числовой
ряд.
Число ![]() называется
называется ![]() -ой
частичной суммой ряда
-ой
частичной суммой ряда ![]() .
.
Сумма
(числового) ряда —
это предел частичных сумм ![]() ,
если он существует и конечен. Таким
образом, если существует число
,
если он существует и конечен. Таким
образом, если существует число ![]() ,
то в этом случае пишут
,
то в этом случае пишут ![]() .
Такой ряд называется сходящимся.
Если предел частичных сумм не существует
или бесконечен, то говорят, что
ряд расходится.
.
Такой ряд называется сходящимся.
Если предел частичных сумм не существует
или бесконечен, то говорят, что
ряд расходится.
Необходимый признак сходимости ряда
Ряд ![]() может сходиться лишь в том случае, когда
член
может сходиться лишь в том случае, когда
член ![]() (общий
член ряда) стремится к нулю:
(общий
член ряда) стремится к нулю:
![]()
Это необходимый признак сходимости ряда (но не достаточный!). Если же общий член ряда не стремится к нулю — это достаточный признак расходимости.
[править]Примеры
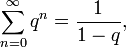 где
где 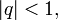 —
сумма геометрической
прогрессии,
в частности
—
сумма геометрической
прогрессии,
в частности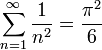 .
.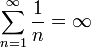 — гармонический
ряд расходится.
— гармонический
ряд расходится.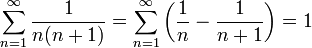 — телескопический
ряд.
— телескопический
ряд.
5.3Абсолютная и простая сходимлсть рядов.
Признаки абсолютной сходимости
[править]Признак сравнения
Если ![]() при
при ![]() ,
то:
,
то:
если ряд
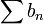 сходится,
то ряд
сходится,
то ряд 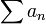 сходится
абсолютно
сходится
абсолютноесли ряд расходится, то ряд расходится
Согласно критерию
Коши, 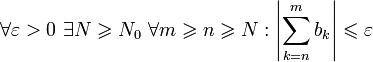 .
Значит,
.
Значит, 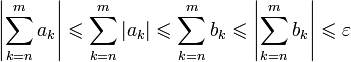 ,
и по критерию Коши ряд
сходится.
Второе утверждение следует из первого,
так как если бы ряд
сходился,
то и ряд
сходился
бы.
,
и по критерию Коши ряд
сходится.
Второе утверждение следует из первого,
так как если бы ряд
сходился,
то и ряд
сходился
бы.
[править]Признак сходимости рядов с монотонно убывающими членами
Пусть ![]() .
Тогда ряд
.
Тогда ряд ![]() сходится
тогда и только тогда, когда сходится
ряд
сходится
тогда и только тогда, когда сходится
ряд ![]() Простейшие свойства сходящихся рядов.
Простейшие свойства сходящихся рядов.
1. Если ряд сходится, то сходится любой из его остатков. Наоборот, из сходимости какого-то остатка вытекает сходимость всего ряда. Отсюда следует, что изменение или выбрасывание конечного числа членов ряда не изменяет его сходимости или расходимости.
2. Если
ряд ![]() сходится,
то
сходится,
то ![]() .
.
3. Если
ряд
сходится,
то сходится ряд 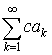 и
имеет место равенство
и
имеет место равенство
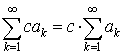 .
.
4. Если
ряды
и ![]() сходятся,
то сходится и ряд
сходятся,
то сходится и ряд 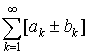 имеет
место равенство
имеет
место равенство
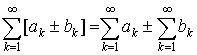 .
.
5. Если
ряд
сходится,
то ![]() .
.
Отсюда
следует Признак
расходимости ряда.
Если ![]() ,
то ряд
расходится.
,
то ряд
расходится.
5.5 понятие и пример условно сходящегося ряда
Ряд ![]() называется условно сходящимся,
если сам он сходится, а ряд, составленный
из абсолютных
величин его
членов, расходится. То есть, если
называется условно сходящимся,
если сам он сходится, а ряд, составленный
из абсолютных
величин его
членов, расходится. То есть, если ![]() существует
(и не бесконечен), но
существует
(и не бесконечен), но ![]() .
Примеры
.
Примеры
Простейшие примеры условно сходящихся рядов дают убывающие по абсолютной величине знакочередующиеся ряды. Например, ряд
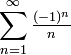
сходится лишь условно, так как ряд из его абсолютных величин — гармонический ряд — расходится.
