4.4 Нахождение функции по ее полному дифференциалу

4.5 Типы поверхностного интеграла

1. Поверхностные интегралы первого типа

К понятию интеграла по поверхности приводит, например, задача о вычислении массы, распределённой по поверхности   с переменной поверхностной плотностью f(M).

Решим эту задачу.

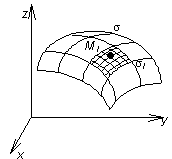Рис.1

Разобьём поверхность   произвольным образом на п частей  i (см. рис. 1) и выберем в каждой из них (также произвольно) точку M_i. Если части  i достаточно малы, то за их массу можно принять произведение  , i = 1, 2, …, n, где  - площадь i-го участка поверхности (т.е. мы предполагаем, что каждый из участков  i однородный с плотностью f(M_i), где i = 1, 2, …, n), тогда масса всей поверхности

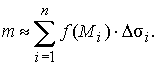 (1)

Это значение тем точнее, чем меньше участки  i. Переходя к пределу при  , а значит, уменьшая размер каждого участка, получим точное значение массы поверхности

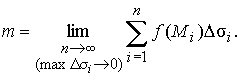
К аналогичным пределам приводят и другие задачи физики, эти пределы называются поверхностными интегралами первого типа.

Теорема. Если при стремлении диаметров всех частей  i к нулю интегральная сумма (1) имеет конечный предел, не зависящий ни от способа разбиения поверхности   на части, ни от выбора точек M_i, то этот предел называется поверхностным интегралом первого рода и обозначается

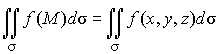 (2)

Заметим, что этот интеграл обладает всеми свойствами криволинейного интеграла первого типа и, в частности, если подынтегральная функция f(x, y, z) = 1, получаем формулу для вычисления площади поверхности 

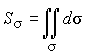. (3)

Интегралу (2) можно придать механический смысл: если f(x, y, z) =   - переменная плотность материальной поверхности  , то масса этой неоднородной поверхности

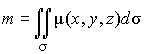. (4)

Выведем формулу для вычисления интеграла (2).

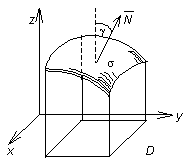Рис.2

Пусть поверхность   однозначно проектируется в область D плоскости хоу. Тогда

,

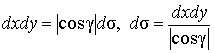где   - угол между нормалью   к поверхности   и осью OZ (см. рис. 2).

Если поверхность   описывается уравнением z = z(x, y), то

(см. тему 12 формулу 14 .).

Подставив этот дифференциал в (2), получим формулу для вычисления поверхностного интеграла по поверхности 

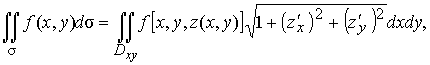(5)

где D_xy - проекция поверхности на плоскость хоу.

Таким образом, чтобы вычислить поверхностный интеграл первого типа, необходимо перевести его в двойной интеграл по области D, полученной в результате проектирования поверхности   на одну из координатных плоскостей (проектирование должно быть взаимно однозначным: одна точка поверхности проектируется в одну точку плоскости), подсчитать элемент   и выразить подынтегральную функцию через выбранные переменные.

Поверхностный интеграл второго типа (по проекциям)

Пусть в каждой точке двухсторонней поверхности   задана непрерывная функция f(x, y, z). Выберем на поверхности определённую сторону, разобьём её сетью произвольных кривых на п участков , на каждом из которых произвольно выберем точку

, где i = 1, 2, …, n.

Вычислим значения функции f_i = f(M_i), где i = 1, 2, …, n.

На каждом из участков   в выбранной точке M_i построим к выбранной стороне поверхности нормаль  .

Спроектируем каждый из участков  _i на плоскость xoy, обозначив   площадь проекции i-го участка. Составим произведения  , причём, если нормаль   образует острый угол с осьюoz, берём произведение со знаком плюс, если нормаль образует тупой угол с осью oz, берём произведение со знаком минус. Суммируем все произведения:

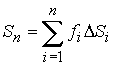.     (6)

Обратите внимание: слагаемые суммы (6), в отличие от предыдущих интегральных сумм, распространяют на весь участок  _i не только значение функции f(M_i), но и направление нормали, построенной в точке M_i.

Теорема. Если существует конечный предел интегральной суммы (6) при стремлении к нулю диаметров всех частей   (или maxdi   0), не зависящий от типа разбиения и выбора точек M_i, то его называют поверхностным интегралом второго типа, распространённым на выбранную сторону поверхности, и обозначают

,

.

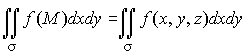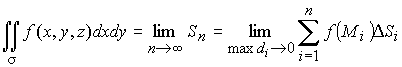Аналогично определяются интегралы

,  ,

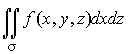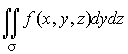причём для выбора знака проекции служит угол нормали с осью оу и ох соответственно.

Наиболее общим видом поверхностного интеграла второго типа является составной интеграл

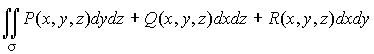, (7)

где Р, Q, R - функции трёх переменных, определённые и непрерывные на поверхности  .

Поверхностный интеграл (7) обладает всеми свойствами поверхностного интеграла первого типа, за исключением одного: при изменении стороны поверхности интеграл меняет знак на противоположный.

Рассмотрим сначала третье слагаемое формулы (7) и поставим задачу о вычислении данного интеграла.

Пусть поверхность   задана уравнением z = f (x, y) и она однозначно проектируется в область D_xy плоскости xoy. Тогда

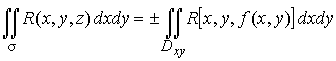, (8)

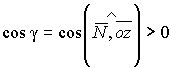где знак (+) берётся, если   на выбранной стороне поверхности  , и знак (-) берётся, если  .

Аналогично рассуждая, получим формулы для вычисления оставшихся слагаемых составного интеграла.

Пусть поверхность   задана уравнением y =  (x, z) и она однозначно проектируется на плоскость xoz в область D_xz. Тогда

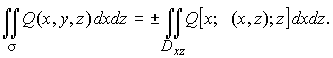 (9)

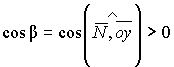Знак (+) берём, если   на выбранной стороне поверхности  , и знак (-) берём, если  .

Первое слагаемое формулы (7) вычисляется с помощью двойного интеграла

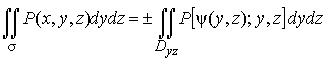, (10)

где x =   (y,z) - уравнение поверхности  ;

D_yz - проекция поверхности   на плоскость yoz.

Знак (+) берём, если 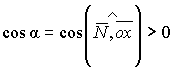 , знак (-) берём, если   на выбранной стороне поверхности  .

Таким образом, для вычисления составного интеграла (7) используются формулы (8) - (10), правые части которых представляют собой двойные интегралы по соответствующим проекциям поверхности   на координатные плоскости; проектирование каждый раз предполагается однозначным. В более сложных случаях поверхность разбивают на части.