Криволинейный интеграл второго типа (по координатам)

В пространственной области Т рассмотрим три функции P(x, y, z), Q(x, y, z), R(x, y, z), непрерывные на дуге АВ кусочно-гладкой кривойL.

Разобьём дугу АВ точками M_i(x_i, y_i, z_i) на п элементарных дуг M_i-1M_i (i = 1, 2, …, n), на каждой из которых произвольно выберем точкуK_i. Вычислим значения каждой из функций в выбранных точках

P(K_i), Q(K_i), R(K_i) где i = 1, 2, …, n.

Спроектируем каждую элементарную дугу на оси координат, обозначив их проекции соответственно . Составим произведения

для всех i = 1, 2, …, n и просуммируем их:

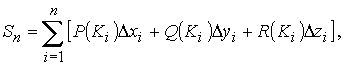 (5)

где S_n- интегральная сумма для функций P, Q, R.

Определение. Криволинейным интегралом второго типа, взятым по кривой L (или по пути АВ), называется предел интегральной суммы S_n при   и

Обозначается:

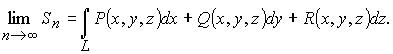 (6)

В частности, в двухмерном пространстве, если кривая L целиком находится в плоскости хоу, а функции P, Q, R не зависят от переменной z, имеем криволинейный интеграл

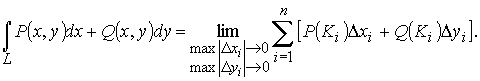
Докажем, что составной интеграл существует, и одновременно получим метод его вычисления.

4.3 Критерий независимости криволинейного интеграла второго типа от пути

Независимость криволинейного интеграла от пути

         Среди силовых полей в физике особую роль играют так называемые потенциальные силовые поля. Их отличительной особенностью является то, что работа, совершаемая таким полем, зависит лишь от начальной и конечной точек пути, и не зависит от траектории, соединяющей эти точки. Математически это соответствует тому, что криволинейный интеграл второго рода также зависит лишь от начальной и конечной точек пути, и не зависит от траектории, соединяющей эти точки. Поэтому с математической точки зрения представляет интерес выяснение тех условий, при выполнении которых криволинейный интеграл обладает этим свойством.

1Плоский случай

         Пусть дан криволинейный интеграл второго рода по плоской кривой

.

Ответ на поставленный вопрос дают следующие две теоремы.

         Теорема 1. Для того чтобы   не зависел от пути интегрирования необходимо и достаточно, чтобы существовала такая функция  , что

.

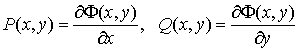         Теорема 2. Если в односвязной области существуют и непрерывны 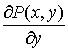  и  , то для того, чтобы было выполнено условие теоремы 1, необходимо и достаточно, чтобы

.

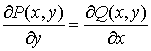2Пространственный случай

         В случае интегралов по пространственной кривой соответствующие теоремы приобретают следующий вид.

         Теорема 1. Для того чтобы   не зависел от пути интегрирования необходимо и достаточно, чтобы существовала такая функция,   что  .

         Для формулировки второй теоремы введем понятие ротора векторной функции. Пусть   . Тогда ротор этой функции определяется так:

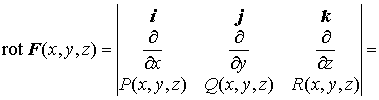
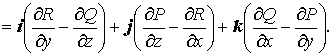
Теорема 2. Для того чтобы   не зависел от пути интегрирования необходимо и достаточно, чтобы выполнялось условие

. 

4.2 физический смысл криволинейного интеграла второго типа

Физический смысл

         Рассмотрим криволинейные интегралы второго рода по пространственной кривой

.

Рассмотрим так называемую вектор-функцию

как трехмерный вектор с компонентами  ,    и  , а также вектор  . Тогда комбинация, стоящая под знаком интеграла, есть не что иное, как скалярное произведение   и  , то есть

,

и поэтому

.

         Физически вектор-функция   ассоциируется с силовым полем, когда в каждой точке пространства на материальную точку действует сила  . Примером такого поля может служить гравитационное поле, электрическое поле, магнитное поле и т.д. Физически скалярное произведение   имеет смысл работы, которую силовое поле   совершает, перемещая материальную точку по вектору dr. Поэтому, с точки зрения физика, криволинейный интеграл второго рода

есть работа, которую совершает силовое поле  , перемещая материальную точку по кривойАВ.

         Обозначим через a, b и g углы, которые вектор   образует с осями OX, OY и OZ. Заметим, что длина вектора 

есть не что иное, как дифференциал длины дуги кривой. Поэтому

и мы можем записать

.

Заметим, что слева стоит криволинейный интеграл второго рода, а справа – криволинейный интеграл первого рода. Эта формула, таким образом, дает связь между криволинейными интегралами первого и второго рода.