7.3. Числовое программное управление
Система управления, работающие по программе, заданной в цифровом виде, называются системами с числовым программным управлением (ЧПУ). Они широко применяются в металлорежущих станках, в некотором технологическом оборудовании, в промышленных роботах. Основное достоинство этого способа – возможность быстрой подготовки и смены программы. Поэтому оборудование с ЧПУ удобно использовать при серийном и мелкосерийном производстве. Однако оно еще достаточно дорого.
При задании программы в цифровом виде программоносителем является в простейшем случае перфолента или магнитная лента.
Информация о величине требуемого перемещения каждого исполнительного органа задается в виде информационного числа Z.
Z = S / ∆S,
где S – величина требуемого перемещения,
∆S – величина единичного перемещения, шаг.
Для того чтобы реализовать шаговые перемещения, чаще всего используются шаговые электрические двигатели. Цепь питания этих двигателей включается импульсами, при каждом включении ротор поворачивается на определенный угловой шаг (рис. 7.5).
Рис. 7.5. Схема шагового электродвигателя
Полюса статора представляют электромагниты. Они разделены вдоль оси статора на секции I II III. Ротор также состоит из секций, которые представляют постоянные магниты с числом зубцов равным числу полюсов статора. Секции ротора повернуты друг относительно друга на одну треть полюсного угла α.
Если подать импульс постоянного тока на первую секцию, то вследствие притяжения разноименных полюсов они установятся друг против друга, а полюса второй и третьей секций расположатся со смещением на углы 1/3α и 2/3α. Если отключить первую секцию и включить вторую, то под действием электромагнитных сил полюса во второй секции установятся друг против друга, а ротор повернется на угол 1/3α. Затем, если выключить вторую и включить третью секцию, ротор повернется на угол 2/3α.
При переключении с первой секции на вторую и третью ротор вращается против часовой стрелки. При переключении с первой секции на третью, а затем вторую – по часовой стрелке. Скорость вращения ротора определяется частотой поступающих в двигатель импульсов тока, а общий угол поворота определяется количеством импульсов.
7.4. Система управления по времени
Графическое изображение рабочего цикла машины – автомата в масштабе времени дается цикловой диаграммой (циклограммой). Циклограммы могут быть линейными или круговыми. Циклограмма дает картину состояния исполнительных органов с их увязкой во времени. Циклограммой оговариваются не законы движения, а только сам факт движения и его направление. На линейных циклограммах движение обычно обозначается наклонными линиями, а покой – горизонтальными и поясняются соответствующими подписями. На циклограмме можно привести и другую полезную информацию
Циклограмма – это есть программа для системы управления по времени.
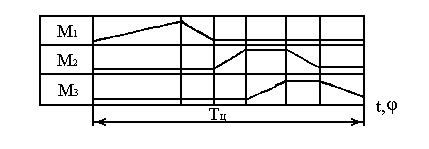
Рис. 7.6 .Циклограмма машины-автомата
В качестве примера рассмотрим линейную циклограмму автомата для сверления отверстий (рис. 7.6). Механизм М1 выполняет сверление отверстий, механизм М2 разжимает крепление обработанной детали, механизм М3 снимает деталь и ставит новую. После этого начинается новый цикл.
Наиболее просто блок управления по времени реализуется с помощью кулачкового распределительного вала, вращающегося с постоянной скоростью. Полный поворот вала осуществляется за время Тц. Включение отдельных исполнительных органов осуществляется с помощью кулачков, повернутых друг относительно друга на углы пропорциональные соответствующим временным интервалам на циклограмме. В таком случае включение механизмов будет происходить в нужные моменты времени. Углы установки кулачков замеряются между начальными прямыми, т.е. прямыми, соответствующими началу подъема толкателя (рис. 7.7). Для кулачкового механизма с центральным толкателем и для одинаковых кулачковых механизмов с коромыслом углы установки кулачков совпадают с углами на циклограмме. Если используются неодинаковые кулачковые механизмы, углы установки определяются графическими построениями или аналитически.
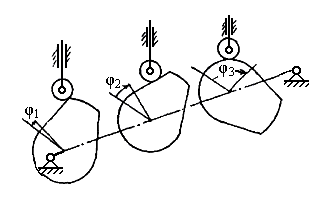
Рис. 7.7. Кулачковый распределительный вал
Анализируя циклограмму можно установить, что некоторые движения могут быть полностью или частично совмещены во времени. Появляется возможность уплотнить циклограмму, тем самым уменьшить Тц, что положительно сказывается на производительности машины.
Кулачковый распределительный вал выполняет две функции: функцию программоносителя и функцию передаточного механизма от двигателя к исполнительному органу. Возникающие при этом большие нагрузки снижают долговечность механизма. От этого недостатка свободен кулачковый командоаппарат. Он состоит из равномерно вращающегося кулачкового распределительного вала, воздействующего на переключатели, которые управляют индивидуальными приводами исполнительных органов.
7.5. Основы синтеза логических систем управления
При синтезе систем управления машин – автоматов часто требуется осуществить определенную последовательность работы исполнительных органов при изменяющейся длительности и изменяющихся параметрах технологического процесса. Использовать описанную выше систему с кулачковым распределительным валом нельзя, т. к. они пригодны только для жестко регламентированных по времени и неизменных по структуре процессов. Такие системы управления реализуются с помощью логических устройств. Действие их подчиняется законам алгебры логики или булевой алгебры. Изложим некоторые основные положения этой алгебры.
Ее отличие от обычной алгебры состоит прежде всего в том, что в ней переменные и их функции могут принимать только два значения, 0 и 1. Поэтому эта алгебра еще называется двоичной, а переменные и функции – двоичными.
Простейшими логическими функциями являются функция повторения (ДА), отрицания (НЕ), умножения (И), сложения (ИЛИ). Для обозначения логических операций используются соответствующие символы. Функция повторения f = x означает, что значение переменной сохраняется. Функция отрицания f = x означает, что значение переменной x отрицается, т.е., если x = 1, то f = 0, если x = 0, то f = 1. Функция умножения f = x1 x2 означает, что f = 1 в том и только в том случае, если x1 и x2 одновременно равны 1. Функция сложения f = x1 + x2 означает, что f=1, если равна 1 хотя бы одна из переменных. На основании простейших логических функций могут быть построены более сложные функции.
Применение двоичной алгебры к задачам управления объясняется тем, что для исполнительных органов характерны два состояния – начало и конец движения. Электрические (пневматические, гидравлические) цепи, управляющие работой исполнительных органов, могут находиться только в двух состояниях – есть ток (давление) или нет тока. Эти два состояния можно описать сигналами, принимающими значения 0 и 1.
В системах управления машин – автоматов значения аргументов представляют собой входные сигналы, а значения функций – выходные сигналы. Каждому набору входных сигналов соответствует определенное состояние системы управления.
Логические функции можно задавать как в алгебраическом, так и в табличном виде. В качестве примера в таблице 7.1 представлены функции f = x1 x2 x3 и f2 = x1 x2 x3.
Таблица 7.1
|
x1 |
x2 |
x3 |
f1 = x1 x2 x3 |
f2 = x1 x2 x3 |
1 |
1 |
1 |
1 |
1 |
0 |
2 |
1 |
0 |
1 |
0 |
0 |
3 |
0 |
1 |
1 |
0 |
0 |
4 |
0 |
0 |
1 |
0 |
0 |
5 |
1 |
1 |
0 |
0 |
0 |
6 |
1 |
0 |
0 |
0 |
0 |
7 |
0 |
1 |
0 |
0 |
1 |
8 |
0 |
0 |
0 |
0 |
0 |
Эта таблица называется таблицей состояний. По функции, заданной в алгебраическом виде, несложно составить таблицу состояний, обратное преобразование сделать труднее. При синтезе систем управления возникает задача составления выражений, называемых формулами включения, по известной таблице состояний.
Физическая реализация логических функций возможна с помощью устройств, которые могут находиться в двух конечных состояниях. Такие устройства называются реле или логические элементы. Оформлены они могут быть по разному. Применяются механические, электрические, пневматические, полупроводниковые, магнитные и др. логические элементы. Логические элементы, реализующие простейшие логические функции, выпускаются серийно. Они служат основой для создания автоматических устройств, реализующих сложные логические функции. Из всего многообразия логических элементов для примера рассмотрим электрические и электромагнитные, которые применяются наиболее часто (рис. 7.8).
Рис. 7.8. Электрические и электромагнитные логические устройства
Электрический логический элемент повторения представляет нормально разомкнутый электрический выключатель (кнопку). При нажатии на него (x = 1) цепь замыкается (f = 1).
Электромагнитное реле того же назначения имеет замыкающте контакты, срабатывающие при перемещении якоря электромагнита. При наличии тока в обмотке электромагнита (x = 1) цепь замыкается (f = 1). В обоих устройствах, если нет сигнала (x = 0), цепь разомкнута (f = 0).
Электрический логический элемент отрицания представляет нормально замкнутый выключатель. При нажатии на него (x = 1) цепь размыкается (f = 0). Электромагнитное реле имеет контакты, которые при появлении тока в обмотке электромагнита размыкаются.
Логические элементы сложения и умножения представляют соответственно последовательно и параллельно соединенные нормально открытые электрические контакты или электромагнитные реле с замыкающими контактами.