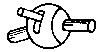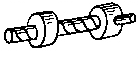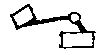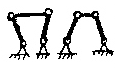211

ПРЕДИСЛОВИЕ

Основу данного учебного пособия составили лекции, читаемые автором на протяжении многих лет студентам Могилевского машиностроительного института, ныне технического университета. В последние годы курс теории механизмов и машин претерпел значительные изменения. В частности, в нем появились разделы, посвященные роботам и манипуляторам. Ввиду особой важности этого вида техники для машиностроительного производства будущего, студенты должны в самом начале своего технического образования получить некоторые сведения о роботах с тем, чтобы закрепить их впоследствии при изучении специальных дисциплин. Сам курс теперь получил название

«Теория механизмов, машин и манипуляторов». Отличие настоящего пособия от аналогичных прежде всего состоит в том, что в нем во всех разделах уделено должное внимание этой новой для традиционного курса теме.

Другая особенность курса состоит в том, что он сопровождается электронным вариантом, размещенным на сайте университета и к которому могут иметь доступ все желающие. Это позволяет использовать его для развития новых технологий обучения. Кроме того, методические разработки последних лет, включая лабораторные работы , практические занятия и, в определенной степени, курсовое проектирование , выполненные на кафедре, в значительной мере базируются на этом курсе.

В связи с ограниченным объемом часов, выделяемым учебным планом на всю дисциплину , не весь приводимый в пособии материал обязателен для освоения студентами . Мелким шрифтом в пособии выделен материал, который по мнению автора полезен для более глубокого ознакомления с предметом, но не обязателен для сдачи экзамена. Сюда в частности относятся некоторые специальные вопросы кинематики рычажных механизмов и некоторые разделы динамики.

ВВЕДЕНИЕ

Теория механизмов , машин и манипуляторов является общеинженерной дисциплиной, играющей роль связующего звена между циклом общенаучных и специальных дисциплин. Вместе с курсом теоретической механики, сопротивления материалов и деталей машин она образует группу предметов, закладывающих фундамент инженерного образования машиностроительного профиля. Значение этих дисциплин не снижается, а растет.

Курс «Теории механизмов, машин и манипуляторов» (сокращенно ТМММ) иногда называют механикой машин, тем самым подчеркивая, что это специальный раздел механики, изучающий присущими механике методами системы машин и механизмов.

ТМММ изучает общие свойства механизмов и машин, дает общие методы их проектирования, пригодные для различных областей техники. ТМММ обычно ограничивается только схемными решениями, так как именно схемы определяют основные параметры механизма. Никакими конструктивными и технологическими улучшениями нельзя исправить недостатки схемы. Сведения, содержащиеся в курсе ТМММ, важны не только для конструкторов, но и для эксплуатационников, так как грамотная эксплуатация возможна только при четком понимании принципов работы и основных свойств машин.

Все задачи курса ТММ можно условно разделить на две категории: задачи анализа и задачи синтеза.

Анализ состоит в исследовании кинематических и динамических свойств механизма по заданной схеме механизма и заданным размерам. Задача синтеза является обратной по отношению к задаче анализа. Однако не всегда существуют методы прямого решения задачи синтеза. Поэтому при проектировании приходится прибегать к многократному повторению задачи анализа с тем, чтобы выбрать из рассматриваемых вариантов наилучший.

Настоящий курс состоит из следующих разделов: Основы структурного анализа механизмов; Кинематика механизмов; Динамический анализ машин и механизмов; Синтез рычажных механизмов; Синтез зубчатых механизмов; Синтез кулачковых механизмов; Основы теории машин – автоматов; Роботы и манипуляторы.

Слово «механика» происходит от древнегреческого слова, которым называлось все искусно придуманное. В русском языке еще во времена Петра I это слово звучало как «махина».

История машин имеет древние корни. В процессе овладения природой первобытный человек начал проникать вначале бессознательно, интуитивно в ее тайны.

Около 7 тыс. лет назад возникают первые цивилизации (Нил, Тигр и Евфрат, Инд, Желтая река). В 5 –ом тысячелетии до н. э. человек познакомился с бронзой, во 2-ом тысячелетии до н. э. – с железом. Уже тогда люди умели пользоваться рычагом и клином. Затем они овладели вращательным движением. Очень древнее происхождение имеют зернотерки. В 5 – 3 в.в. до н. э. появилась водяная мельница – первая машина в мировой истории. Вращение деревянной палочки для получения огня, гончарный круг, бревно для перевозки тяжестей, подъемные приспособления, блок и ворот, наконец колесо – первые практические результаты освоения вращательного движения, достигнутые на рубеже 1-го тысячелетия.

Водяная мельница состояла из энергетического агрегата – водяного колеса, передачи – два цевочных колеса, рабочего органа – жернова. В таком же виде она просуществовала до 18 –19 в.в.. Возникновение водяной мельницы обусловлено потребностью населения в муке. Другая причина возникновения машин – нужды войны. Древнейшие из таких машин – баллисты, метали камни массой до 30 кг на 400 м.

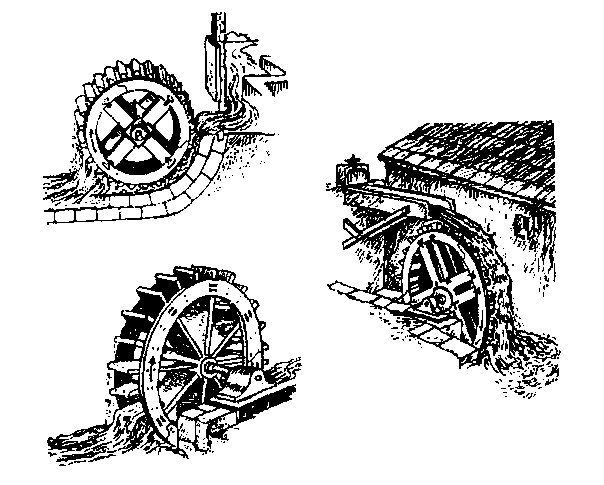
Водяная мельница

Величайшим математиком и механиком античности был Архимед (287 – 212 г.г. до н. э.). Он изобрел винт, усовершенствовал зубчатые колеса, построил водоподъемные сооружения, построил ряд военных машин. Бурное развитие греческой культуры, городов, войны способствовали развитию не только практической механики, но и теории. Филон написал «Свод механики» – девять книг, среди которых, например, были «Учение о рычагах», «О построении метательных машин», « О построении автоматов». Ктесибий (2 –ой в. до н. э.) изобрел поршневой насос, счетчик оборотов. Герон (1-ый в. до н. э.) написал больше всех античных ученых о механике: «Книга о подъемных механизмах», « Книга о военных машинах», « Театр автоматов». Герон описывает простые машины, системы зубчатых колес, системы блоков и полиспастов, «эомпил» - прообраз паровой турбины. «Театр автоматов» описывает храмовые и театральные автоматы, которые в то время пользовались популярностью у населения.

К механике эпохи эллинизма примыкает механика Рима и Карфагена. Подробные сведения об уровне механики того времени содержатся в сочинении Витрувия «Об архитектуре». По определению Витрувия «машина есть прочное соединение деревянных частей, предназначенное для передвижения грузов и приводимое в движение искусственным образом по кругу, что греки называют круговым движением».

Счетчик оборотов (Герон)

В 4 – 5 в.в. н. э. началось великое переселение народов. В 372 г. в Европу вторглись гунны. Под напором гуннов германские племена вторглись в Римскую империю. На ее развалинах возник ряд государств. Цивилизация

переживала глубокий кризис: города пустели, ремесла и торговля замирали, наука не развивалась. Многое из достигнутого было забыто.

Эпоха средневековья продолжалась 1000 лет, с 5 в. по 15в.Она мало что дала не только науке, но и практической механике. Основные технологические машины средневековья – сукновальни, мельницы для изготовления пеньки, железоделательные мельницы (по сути кузнечный молот). В 12 –13 в.в. распространяются бумагоделательные, лесопильные мельницы, они применяются с целью замены физической силы человека. В 15 в. было изобретено книгопечатание. Первым печатным станком был винтовой пресс.

Мельница с коленчатым валом

Со второй половины 15 в. начинается эпоха Ренессанса. «Это был величайший прогрессивный переворот из всех пережитых до того времени человечеством, - писал Энгельс, - эпоха, которая нуждалась в титанах и которая породила титанов по силе мысли, страсти и характеру, по многосторонности и учености… Тогда не было почти ни одного крупного человека, который не совершил бы далеких путешествий, не говорил бы на четырех или пяти языках, не блистал бы в нескольких областях творчества. Леонардо да Винчи был не только великим живописцем, но и великим математиком, механиком и инженером, которому обязаны важнейшими открытиями самые разнообразные отрасли физики…».

Проект экскаватора (Леонардо да Винчи)

В области механики Леонардо первым исследовал полет птиц и приблизился к созданию аппарата тяжелее воздуха. Он создал много различных схем машин, он изучал трение и понял невозможность вечного двигателя за 300 лет до того, как это было доказано. В годы деятельности Леонардо да Винчи уже бытовало слово «инженер», которое обозначало строителя военных машин и фортификаций.

Великие географические открытия 15 – 16 в.в. вызвали приток золота в Европу. Оживилась коммерческая деятельность, развиваются ростки капиталистической мануфактуры в недрах цеховых ремесел. Мануфактура не могла обойтись без развитой механической техники. Наряду с известными возникают новые механизмы, происходит усложнение машин. Этот период совпадает с периодом революции в науке. Он начался с открытий Коперника, «остановившего Солнце и сдвинувшего Землю».

Паровая турбина с зубчатой передачей (XVII в.)

Революция в науке обязана деятельности большого числа ученых, среди которых наиболее выдающимися были Кеплер, Бэкон, Галилей, Декарт, Гюйгенс, Гук, Ньютон, Лейбниц. Значение И.Ньютона для дальнейшего развития науки огромно. Его труд «Математические основания натуральной философии» (1687 г.) как бы завершил научную революцию и явился основой для создания не только ньютоновской механики, но и нового миропонимания. Ее значение для техники и по сей день остается непоколебимым.

Прядильная машина (Кромптон)

За революцией в науке последовала революция в технике. В 30-х годах 18 в. в Англии изобрели технологические машины, которые смогли заменить уже не только физическую силу человека, но и его руки. Так, в 1735 г. была изобретена прядильная машина. Появление технологических машин заставило подумать об универсальном двигателе. Это привело к изобретению паровой машины. Джеймс Уатт после большой серии экспериментов усовершенствовал паровую машину. Производство паровых машин в конце 18 в. стало государственным секретом Англии, и вывоз их был запрещен. Строительством паровых машин стали заниматься и в других странах.Следует отметить, что первыми изобретателями паровых машин были И.Ползунов (1765г.) и Т. Ньюкомен ( 1722 г.)

Паровая машина позволила строить предприятия не только на берегах рек. Началось использование машин для производства самих машин. Началось развитие механического транспорта: локомотивов, пароходов.

Одновременно происходит становление механики машин как науки Первые курсы – Ж.Ашетт «Элементарный курс машин», Р.Виллис «Принципы механизмов». Большой вклад внесли Г.Кориолис, Ж.Понселе (Франция), П.Л.Чебышев, Н.Е.Жуковский (Россия), Ф.Рело, Л.Бурмейстер (Германия).

На протяжении 25 лет (1890 – 1915 г.г.) техника решила задачи эпохального значения: создан двигатель Дизеля; созданы паровые турбины; изобретен автомобиль; изобретено радио; началось развитие авиации; усовершенствованы машины для обработки металлов.

Основателем русской школы теории механизмов и машин является замечательный математик, академик П.Л.Чебышев, В теоретическом плане П.Л.Чебышев занимался проблемами синтеза механизмов, тесно связав их решение с созданной им теорией приближения функций. Кроме того, известен ряд замечательных изобретений П.Л.Чебышева, относящихся к практической механике: приближенное прямило, паровая машина, центробежный регулятор, самокатное кресло, «стопоход» - предшественник шагающих механизмов.

Большой вклад в развитие теории механизмов внес «отец русской авиации» проф. Н.Е.Жуковский. Им, в частности, предложен способ силового исследования, изучаемый в настоящем курсе механизмов, носящий название теоремы о жестком рычаге. Идеи проф. Ассура, относящиеся к структуре механизмов, позволили создать современную классификацию рычажных механизмов.

Паровая машина (Уатт)

Академик И.И. Артоболевский написал основной современный учебник по ТММ. Им также составлен многотомный справочник «Механизмы в современной технике», являющийся своего рода энциклопедией по механизмам.

1. ОСНОВЫ СТРУКТУРНОГО АНАЛИЗА МЕХАНИЗМОВ

1.1.Основные понятия курса теории механизмов , машин и манипуляторов

Само название курса указывает на то, что делается различие между понятиями «механизм» и «машина». Содержание этих понятий изменялось в процессе развития техники. К настоящему времени утвердились следующие определения:

«Машина есть устройство, выполняющее механические движения для преобразования энергии, материалов и информации с целью замены или облегчения физического и умственного труда человека».

«Механизм есть система тел, предназначенная для преобразования движения одного или нескольких тел в требуемое движение других тел».

Из этих определений следует, что в машине происходит преобразование энергии, материалов или информации, а в механизме – только преобразование параметров или одного вида механического движения в другой. Как правило механизмы входят составными частями в машину, так что понятие «машина» является более широким, чем «механизм».

Машины принято делить на энергетические, технологические, транспортные, информационные, машины-автоматы, манипуляторы. К энергетическим машинам относят электродвигатели, турбины, двигатели внутреннего сгорания, паровые машины; к технологическим – металлорежущие станки, машины текстильного производства, т.е. все те устройства, посредством которых выполняются преобразования материалов; к транспортным машинам – автомобили, самолеты, локомотивы, подъемные краны, лифты; к информационным – устройства для переработки информации, например механические калькуляторы, дифференцирующие и интегрирующие устройства , а также современные компьютеры; к машинам–автоматам относятся устройства, в которых преобразование энергии, материалов или информации осуществляется без участия человека; к манипуляторам относятся устройства, воспроизводящие двигательные функции человеческих рук.

В зависимости от того, в каком виде существуют тела передающие движение – твердом, жидком или газообразном, механизмы принято делить на механизмы с твердыми звеньями, гидравлические и пневматические механизмы. В курсе ТММ рассматривается только первый тип механизмов, гидравлические и пневматические механизмы подробно изучаются в специальных курсах.

Познакомимся с некоторыми основными понятиями и определениями ТММ.

Звеном называется одна или несколько жестко связанных между собой деталей, Под деталью понимается отдельно изготавливаемая часть механизма. Все детали, входящие в звено, движутся как одно целое.

Звено, относительно которого изучается движение остальных звеньев механизма, называется стойкой. Пользуясь языком теоретической механики, можно сказать, что со стойкой связана система координат, относительно которой рассматривается движение остальных звеньев механизма

Входным звеном называется звено, которому сообщается движение, преобразуемое затем в требуемые движения других звеньев. Выходным звеном называется звено, которое совершает движение, для которого и предназначен механизм. Чаще всего применяют механизмы с одним входным и одним выходным звеном, но бывают механизмы и с большим числом таких звеньев – их называют дифференциалами. Входное звено соединено с двигателем, выходное – с рабочим органом машины. Остальные звенья, участвующие в передаче движения называются промежуточными.

Фундаментальным понятием ТММ является понятие «кинематическая пара». Теорию механизмов иногда даже называют теорией кинематических пар.

Кинематической парой называется соединение двух звеньев, допускающее их относительное движение. Следует подчеркнуть, что кинематическая пара это не два звена, как воспринимается это в тривиальном смысле, а одно соединение. В этом источник многих ошибок, совершаемых студентами, при структурном анализе механизмов. Точки, линии, поверхности, по которым происходит соприкосновение звеньев в кинематической паре, называются элементами кинематической пары.

Структурной схемой механизма называется упрощенное графическое изображение механизма, на котором звенья условно изображаются отрезками прямых, треугольниками, прямоугольниками, окружностями и обозначаются арабскими цифрами, а кинематические пары условно изображаются согласно принятым правилам и обозначаются большими латинскими буквами. Имеется соответствующий стандарт, регламентирующий условные изображения звеньев на схемах.

Кинематической схемой называется структурная схема, построенная с соблюдением относительных размеров звеньев в некотором масштабе, Следует различать структурную и кинематическую схему - часто эти понятия путают.

Есть еще одна схема – конструктивная. Это изображение механизма с соблюдением основной формы деталей и относительных размеров, часто изображение в аксонометрии.

1.2. Виды и классификация кинематических пар

Как известно из теоретической механики, свободное твердое тело, находящееся в трехмерном пространстве обладает 6-ю степенями свободы, т.е. может совершать 6 независимых движений: 3 поступательных вдоль выбранных осей и 3 вращательных вокруг этих же осей. Величины соответствующих перемещений называют обобщенными координатами тела. Если такое тело связать с другим телом посредством кинематической пары, то это уменьшит его число степеней свободы на число связей (запрещений), налагаемых другим телом. Число связей определяется видом кинематической пары.

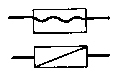
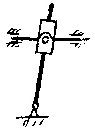
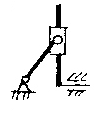
Основные виды кинематических пар и их условные изображения представлены на рис.1.1. Простейшие пары, поступательная и вращательная, накладывают 5 условий связей, оставляя возможным только одно поступательное или одно вращательное движение относительно оси пары.

Класс	Схема	Условное обозначение
3
4
5
5
4
5

Рис. 1.1. Виды кинематических пар

Условие связи, как известно, выражается уравнением относительно обобщенных координат. Кинематические пары принято делить по числу уравнений связей на классы от 5-го до 1-го. Иногда их различают по числу степеней свободы на одно-, двух-, трех-, четырех-, и пяти-подвижные. Подвижность и класс каждой пары в сумме равны 6, т.е. числу степеней свободы свободного твердого тела. Таким образом класс и подвижность по разному характеризуют одно и то же свойство.

Кинематические пары по характеру движения делятся на плоские и пространственные. В плоских парах относительное движение происходит в плоскости (вращательная, поступательная).

По форме элементов (см. выше) кинематические пары делятся на низшие и высшие. В низших парах элементами служат поверхности: плоскости, цилиндрические и сферические поверхности. В высших парах элементами являются точки и линии. Достоинство низших пар – повышенная долговечность соединения благодаря небольшим удельным нагрузкам на поверхность. В высших парах соприкосновение звеньев происходит на небольших площадках, что ведет к их ускоренному износу. Посредством низших пар можно осуществлять относительно простые движения, высшие пары представляют в этом отношении большие возможности.

1.3. Кинематическая цепь. Кинематическое соединение

Кинематическая цепь - это система звеньев, образующих между собой кинематические пары. В зависимости от того, какие кинематические пары присутствуют в цепи и как они расположены, различают плоские и пространственные кинематические цепи. В плоской кинематической цепи все звенья движутся в одной или параллельных плоскостях (рис.1.2,а).

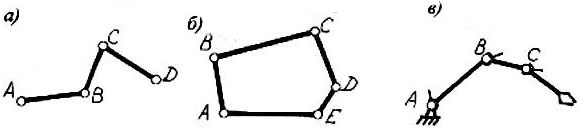
Рис. 1.2. Кинематические цепи: а – плоская, б – замкнутая ,

в- отккрытая

Кинематическая цепь, звенья которой образуют замкнутый контур, называется замкнутой (рис.1.2,б), если контур не замкнут, цепь называется незамкнутой или открытой (рис.1.2,в). В традиционных механизмах обычно используются замкнутые кинематические цепи, незамкнутые цепи находят применение только в манипуляторах. Механизм – это кинематическая цепь, в которой указаны стойка, входные и выходные звенья.

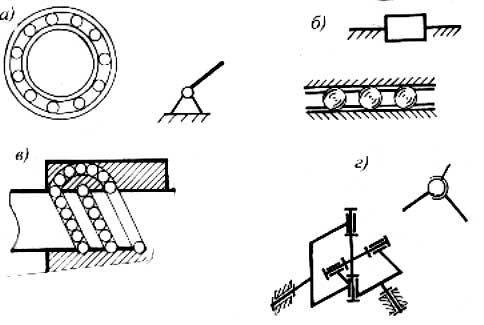
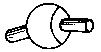
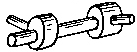
Рис. 1.3. Кинематические соединения: а – шарикоподшипник, б – роликовая направляющая, в - винтовая пара качения, г –универсальный шарнир

На основе кинематических цепей можно получать не только механизмы, но и устройства, заменяющие некоторые кинематические пары, так называемые кинематические соединения (рис.1.3). Шарико- или роликоподшипник эквивалентен вращательной паре. Роликовые направляющие заменяют поступательную пару. Винтовая пара качения заменяет обычную винтовую пару. Карданный шарнир, он же называется шарниром Гука или универсальным шарниром, заменяет сферическую пару с пальцем. Если вилку снабдить еще одной вращательной парой получим аналог сферической пары.

1.4. Число степеней свободы механизма

Кинематическая цепь составляет основу каждого механизма. Важнейшей характеристикой кинематической цепи является число степеней свободы.

В теоретической механике под числом степеней свободы понимается число обобщенных координат, т.е. независимых между собой параметров, определяющих положение системы в выбранном пространстве. Обобщенными координатами механизма называются независимые между собой координаты, заданием которых определяется положение всех звеньев относительно стойки. Число обобщенных координат механизма равно его числу степеней свободы или по другой терминологии – степени подвижности механизма.

Пусть кинематическая цепь содержит n звеньев. До того как они были соединены посредством кинематических пар, система из n звеньев имела 6n координат. Каждая кинематическая пара класса m дает m уравнений связей относительно координат. Разность между числом координат и числом уравнений связей дает число независимых координат:

W= 6n - 5p₁ - 4p₂ - 3p₃ - 2p₄ - p₅ , (1.1)

где W – число степеней свободы механизма; n – число подвижных звеньев; p₁ – число пар 5-го класса (одноподвижных), р₂ – число пар 4-го класса, р₃ – число пар 3-го класса и т.д.

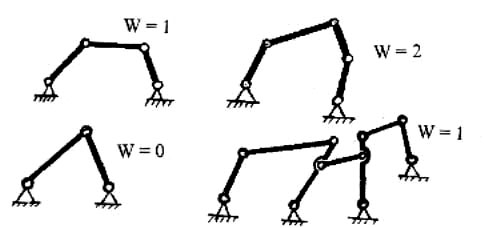
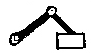
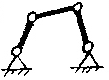
Рис.1.4. Примеры кинематических цепей

Эта формула известна как формула Сомова-Малышева. Для плоского механизма аналогичные рассуждения приводят к формуле Чебышева:

W = 3n – 2p₁ – p₂ . (1.2)

На рисунке 1.4 представлены примеры кинематических цепей с различными степенями подвижности.

Звенья, которым приписываются обобщенные координаты, называются начальными. Обычно они совпадают с входными звеньями, однако есть случаи, когда за начальное звено принимают выходное или даже промежуточное – это упрощает исследование механизма. Число степенй свободы механизма определяет число начальных звеньев. Чаще всего применяют механизмы

с W = 1.

В механизмах с простой замкнутой кинематической цепью и одноподвижными парами число подвижных звеньев на единицу меньше числа . Для пространственного механизма с одноподвижными парами из формулы Сомова-Малышева следует

1 = 6n – 5p₁ . (1.3)

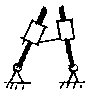
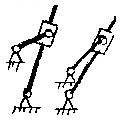
Уравнение (1.3) удовлетворяется при n = 6. Такой механизм называется пространственным семизвенником (рис.1.5,а).

При некоторых частных соотношениях размеров звеньев возможны пространственные механизмы с одноподвижными парами с меньшим числом звеньев: четырехзвенный механизм Беннета (рис.1.5,б), шестизвенный механизм Турбула (рис.1.5,в), сферический четырехзвенник (рис.1.5,г).

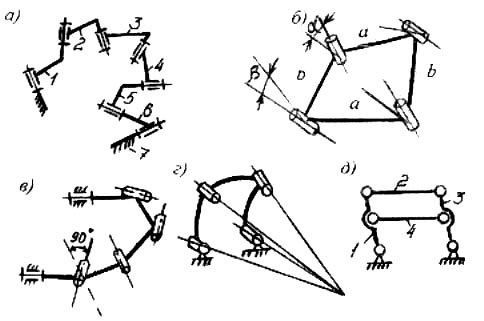
Рис.1.5. Примеры пространственных механизмов

В механизмах могут встречаться избыточные связи. Избыточными называются такие связи, устранение которых не увеличивает числа степеней свободы механизма. Например, в механизме на рис.1.5,д звено 4 может быть удалено, что не отразится на подвижности механизма. Избыточные связи делают механизм более жестким, однако требуют повышенной точности изготовления. В плоских механизмах избыточные связи возникают из-за неточности изготовления звеньев, приводящей к неплоскостности схемы. Избыточные связи в механизмах устраняются путем изменения подвижности кинематических пар.

1.5. Классификация плоских механизмов с низшими парами

Механизмы с низшими парами находят широкое применение в технике. Их принято называть рычажными. Ограничимся пока изучением плоских рычажных механизмов. Рассмотренный ранее четырехзвенный механизм (рис.1.4) является простейшим из них. Более сложные механизмы можно получать, используя метод наслоения групп звеньев.

Каждый механизм с W=1 можно рассматривать состоящим из механизма 1-го класса и присоединенных к нему структурных групп.

Под механизмом 1-го класса понимается начальное звено со стойкой. Механизм 1-го класса имеет W=1.

Структурной (ассуровской) группой называется такая группа звеньев, которая, будучи присоединенной к стойке, образует кинематическую цепь с W=0. Отсюда следует, что

0= 3n – 2p₁ . (1.4)

Уравнение (1.4) есть уравнение структурной группы. Его можно представить в виде:

р₁ = 1.5n . (1.5)

Откуда следует, что в структурной группе число звеньев четное, а число кинематических пар в 1.5 раза больше числа звеньев. Задаваясь разным n, можно получить бесконечно большое число решений (рис.1.6). Практическое значение имеют только два первых решения. Им соответствует двухповодковая группа (диада), и трехповодковая группа (трехповодок). Диада содержит два звена и три кинематические пары. Трехповодок содержит четыре звена и шесть кинематических пар. За счет разного сочетания вращательгых и поступательных пар возникают модификации групп.

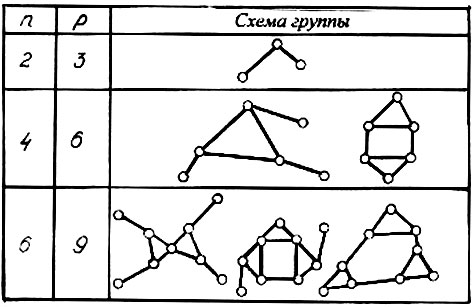
Рис.1.6. Основные структурные группы

По предложению академика И.И.Артоболевского группам и механизмам присвоены классы. Класс группы равен числу кинематических пар, входящих в замкнутый контур, образованный внутренними парами. На этом основании диаду считают группой 2-го класса, а трехповодок – 3-го класса. Класс механизма равен классу старшей группы.

Основное свойство групп состоит в том, что она не изменяет степени подвижности кинематической цепи, к которой она присоединяется. Последовательно наслаивая группу за группой, можно получить разные механизмы. Практическое применение находят механизмы 2-го и реже – 3-го класса.

1.6. Разновидности четырехзвенных рычажных механизмов

В технике наибольшее распространение получили плоские четырехзвенные механизмы. Они образуются путем присоединения к механизму 1-го класса диады. Известно пять модификаций диады, соответственно этому имеются модификации четырехзвенных механизмов, представленные на рис.1.7.

Механизм 1-ой модификации – шарнирный четырехзвенник. Он применяется для изменения параметров вращательного движения или для воспроизведения сложных траекторий. В зависимости от соотношения размеров стойки и остальных звеньев возможны три разновидности шарнирного четырехзвенника: кривошипно-коромысловый механизм, двухкривошипный механизм, двухкоромысловый. Звеньям этих механизмов присвоены специальные названия: кривошип – звено, совершающее полный поворот, коромысло – звено, совершающее неполный поворот, шатун – звено, не образующее кинематических пар со стойкой.

1-ая мод.	2-ая мод.		3-я мод.		4-ая мод.		5-ая мод.

Рис. 1.7. Модификации диад и четырехзвенных рычажных

механизмов

Механизм 2-ой модификации называется кривошипно-ползунным. Он применяется для преобразования вращательного движения в поступательное и обратно. Ползун – звено, образующее поступательную пару со стойкой ( направляющей).

Механизм 3-ей модификации получил название кулисного механизма . Кулисные механизмы предназначены для изменения параметров вращательного движения. Известны разновидности кулисного механизма: с качающейся кулисой и вращающейся кулисой. Кулиса – звено, образующее с другим подвижным звеном, обычно называемым камнем, поступательную пару;

Механизм 4-ой модификации получил название тангенсного механизма, т.к. перемещение ведомого звена представляет функцию tgφ.

Механизм 5-ой модификации – синусный механизм, т.к. перемещение ведомого звена реализует функцию sinφ. Присоединяя диаду 5-ой модификации к механизму 1-го класса другим способом, можно получить механизм Ольдгейма (крестовую муфту), который находит применение для передачи движения при несоосных валах.

1.7. Зубчатые, кулачковые, фрикционные механизмы

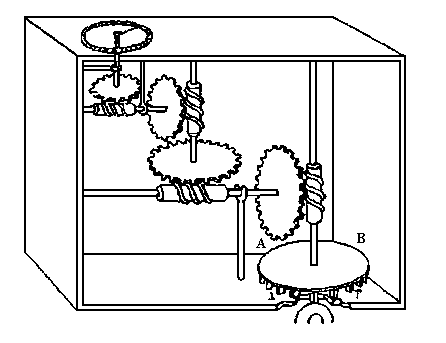
Зубчатым называется механизм, в состав которого входят зубчатые колеса, т. е. звенья с периодически чередующимися выступами (зубьями) и впадинами. Зубья двух колес образуют высшую пару, т.к. касание происходит в точке или по линии вдоль зуба. На схемах зубья не показываются, а зубчатое колесо изображается, так называемой, начальной окружностью. Зубчатые механизмы входят в состав почти каждой достаточно сложной машины. Назначение зубчатых механизмов – уменьшение или увеличение угловой скорости и крутящего момента. Зубчатые механизмы, уменьшающие скорость, называются редукторами. Редукторы применяются в силовых передачах. Механизмы, увеличивающие скорость, называются мультипликаторами. Обычно они используются в приборах для увеличения точности отсчета. В зависимости от схемы зубчатые механизмы делятся на: рядовые зубчатые механизмы и планетарные механизмы (рис.1.8,а, б). Иногда зубчатые механизмы комбинируют с рычажными (рис.1.8,в), в таком случае их называют зубчато-рычажными.

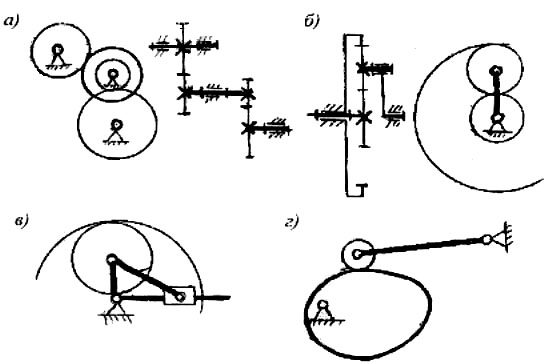
Рис.1.8. Зубчатые и кулачковые механизмы.

Кулачковым называется механизм, в состав которого входит кулачок, т.е. звено с переменной кривизной рабочей поверхности (рис.1.8,г). Выходное звено кулачкового механизма называется толкателем или коромыслом. Кулачок с выходным звеном образует высшую, кинематическую пару. Посредством кулачкового механизма можно осуществить движение по заданному закону, причем синтез таких механизмов относительно несложен.

Механизмы, в которых для передачи движения используются силы трения, называются фрикционными. Такие механизмы удобно применять в тех случаях, когда требуется плавно регулировать скорость выходного звена. Такие механизмы называют вариаторами. Известны дисковые (рис.1.9,а), торовые (рис.1.9,б), валиковые (рис.1.9,в) и другие фрикционные вариаторы. Мощность, передаваемая фрикционными механизмами, относительно невелика. К фрикционным механизмам относятся механизмы, в которых используются гибкие звенья типа ремней, канатов, нитей.

Сравнительно недавно (в 1955 г.) была изобретена волновая передача. Она во многом подобна планетарному механизму, однако работает на эффекте деформации упругого звена. Известны зубчатые, винтовые, фрикционные волновые передачи.

В настоящем курсе ТММ изучаются рычажные, зубчатяе и кулачковые механизмы. Фрикционные механизмы традиционно рассматриваются в курсе «Детали машин».

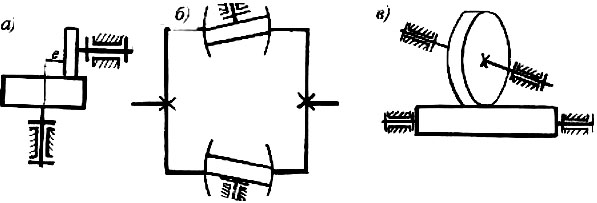
Рис.1.9. Фрикционные механизмы

Контрольные вопросы.

1. Какими признаками должно обладать устройство, чтобы его можно было назвать механизмом ?

2. Что такое звено механизма? Что такое кинематическая пара, каково ее назначение?

3. Какие кинематические пары относятся к низшим, а какие к высшим?

4. Что такое степень подвижности кинематической цепи и как она связана с числом двигателей?

5. Какой механизм называется рычажным?

6. Перечислите разновидности рычажных четырехзвенных механизмов.

7. Запишите формулу Чебышева и разьясните ее содержание.

8. Что такое кинематическое соединение?

9. Что такое структурная группа?

10. Как определяется класс структурной группы?

11. Что такое диада и трехповодок?

12. Как определяется класс механизма?

13. Какой механизм называется зубчатым?

14. Какой механизм называется кулачковым?

15. Приведите пример известного вам механизма и охарактеризуйте его по структурным признакам.

2. Кинематика механизмов

2.1. Задачи кинематики механизмов

Кинематика – раздел механики, изучающий движение без учета причин, вызывающих движение. По своему содержанию она является геометрией движущихся тел. Для характеристики движения используются кинематические параметры: перемещение, скорость и ускорение. Соответственно различают задачи о положениях, о скоростях, об ускорениях.. Решение указанных задач не является самоцелью – они необходимы для последующего полного исследования механизма. Кроме того, кинематика представляет хотя и первую, но важнейшую часть механики машин. В простейших случаях при первоначальном изучении машин можно ограничиться только кинематикой.

Кинематика механизмов в настоящее время изучена достаточно хорошо. Все существующие методы можно разделить на графические и аналитические. Графические методы характеризуются простотой реализации и наглядностью, однако недостаточно точны. Они находят применение на начальных стадиях исследования или для контроля правильности результатов, полученных другими методами. Основным методом для решения инженерных задач является аналитический метод. Он находит широкое применение благодаря распространению вычислительной техники. Метод позволяет получить обширную и точную информацию.

В настоящем разделе изучаются графические методы: метод планов и метод кинематических диаграмм, находящие применение в курсовом проектировании, и аналитический метод – метод преобразования координат. Все эти методы относятся только к механизмам 2-го класса.

2.2. План положений механизма

План положений механизма представляет графическое изображение механизма с соблюдением масштаба при заданных значениях обобщенных координат.

Всякое графическое построение начинается с выбора масштабного коэффициента. Масштабный коэффициент – это отношение истинного значения параметра к длине отрезка, изображающего его на чертеже. Истинное значение параметра берется в свойственных ему единицах измерения, а длина отрезка – в миллиметрах. Здесь используются масштабные коэффициенты длин k_l, скоростей k_v, ускорений k_a. Если, например, обозначить длину кривошипа l_OA, скорость точки А – V_A, ускорение точки А – a_A, а длины отрезков , изображающих их на чертеже, - ОА, pa, πa, то

ķ_l = L_OA/ OA; k_v = V_a / pa; k_a = a_a/πa.

Построение плана положений методом засечек производится в следующей последовательности.

1. Наносятся неподвижные точки механизма (т. О и т. С на рис.2.1).

2. Строится положение начального звена ОА, соответствующее заданной обобщенной координате.

3. Строятся линии возможных положений точек или звеньев механизма (дуги радиусов ВА и ВС).

4. Точки пересечения линий соединяются с другими точками механизма (линии ВА и ВС).

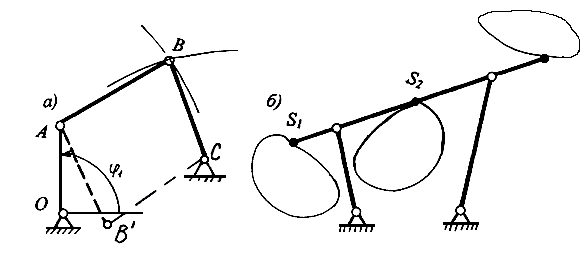
Рис. 2.1. План положения четырехзвенника. Траектории точек

На рис.2.1 имеются две точки пересечения, соответствующие двум возможным положениям механизма. Практически, исключая частные случаи, возможен только один вариант – он определяется сборкой механизма, прямой или обратной. Отмеченное обстоятельство служит геометрической иллюстрацией того, что аналитическое решение задачи о положении такого механизма сводится к квадратному уравнению, имеющему два решения.

Задаваясь разными значениями обобщенной координаты φ, построим план положений механизма. Если соединить одноименные точки в разных положениях механизма плавной кривой, получим их траектории – линии движения точек. Точки на шатуне дают «шатунные кривые», отличающиеся чрезвычайным разнообразием при различных размерах механизма (рис.2.1, б).

2.3. Основные кинематические соотношения

Напомним основные кинематические соотношения, известные из курса теоретической механики. Они лежат в основе построения планов скоростей и планов ускорений.

Плоским или плоскопараллельным называется движение, при котором векторы скоростей и ускорений всех точек параллельны одной плоскости.

Поступательным называется движение, при котором траектории, скорости и ускорения всех точек этого тела одинаковы и тело движется без поворота (рис.2.2 а).

V₁ = V₂ = V₃ = V_A =V_B; a₁ = a₂ = a₃ = a_A = a_B .

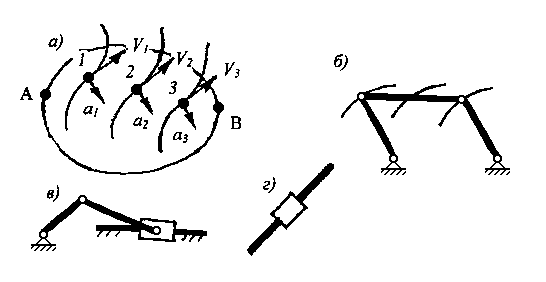
Рис.2.2.Примеры поступательного движения: твердого тела – а, шатуна в шарнирном параллелограмме – б, ползуна в кривошипно-ползунном механизме – в, камня по кулисе -г

Частный случай поступательного движения – прямолинейное движение. Траектории точек в этом случае - прямые линии. Такое движение, например, совершает ползун относительно стойки, камень относительно кулисы. Другой частный случай – круговое поступательное движение. Здесь траектории всех точек –окружности. Так движется шатун шарнирного параллелограмма (рис.2.2, б).

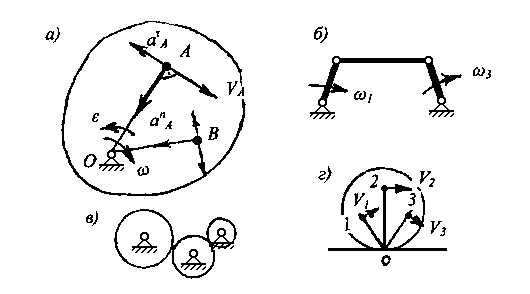
Рис.2.3. Примеры вращательного движения:вращение твердого тела – а, звеньев рычажного механизма – б, звеньев зубчатого механизма – в, колеса по направляющей - г

Вращательным называется движение, при котором одна точка тела неподвижна относительно выбранной системы отсчета (рис.2.3, а). Для скорости и ускорения точки во вращательном движении установлены следующие соотношения:

V_A = ω L_OA; a_A = a_Aⁿ + a_A^τ ;

а_A = ω² L_OA; a_A^τ = ε L_OA; a_A = L_OA (ω⁴+ε²) .

Направление скорости перпендикулярно радиус-вектору точки А и направлено в сторону угловой скорости ω. Нормальное ускорение направлено к неподвижной точке, центру вращения, касательное ускорение перпендикулярно нормальному ускорению и направлено в сторону углового ускорения ε. Вращательное движение совершает кривошип, зубчатые колеса, катящееся по направляющей колесо (рис.2.3 б,в,г).

Сложным называется движение, которое является результатом сложения переносного и относительного движений (рис.2.4). Скорость точки в сложном движении определяется на основании теоремы о сложении скоростей: скорость точки равна геометрической сумме переносной и относительной скорости:

V_A = V^E + V^R .

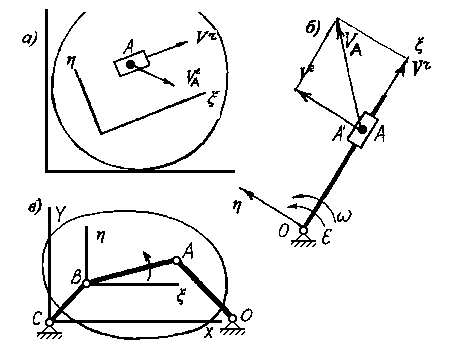
Рис.2.4. Примеры сложного движения: твердого тела – а,

камня по кулисе – б, шатуна в рычажном механизме

Под переносной скоростью понимается скорость той точки переносной системы, которая лежит под точкой А. Такая точка отмечается штрихом (А΄). Точка А΄ движется вместе с переносной системой.

Под относительной скоростью понимается скорость точки А относительно точки А΄. На основании введенных определений вышеприведенную формулу можно записать так:

V_A= V_A' + V_AA' . (2.1)

Ускорение, в сложном движении определяется на основании теоремы о сложении ускорений (теоремы Кориолиса) .

Ускорение точки равно геометрической сумме переносного ускорения, относительного ускорения и кориолисового ускорения, называемого также поворотным или добавочным:

a_A = a^E + a^R + a^K.

Под переносным ускорением понимается ускорение точки А', под относительным – ускорение точки А относительно точки А'. Тогда формулу для ускорения можно представить так :

a_A = a_A' + a_AA' + a^K.

Кориолисово ускорение вызвано с одной стороны изменением направления вектора относительной скорости из-за поворота переносной системы, с другой – изменением величины вектора переносной скорости из-за перемещения точки А' в результате относительного движения. Величина кориолисова ускорения для плоского движения определяется по формуле

a^k = 2 ω V_AA', (2.2)

где ω - угловая скорость переносной системы.

Из формулы (2.2) следует, что a^K = 0, если ω=0 или V_AA' = 0. Направление кориолисова ускорения находится по правилу Жуковского:

вектор относительной скорости V_AA' следует повернуть на 90˚ в сторону вращения переносной системы.

Приведенные выше формулы находят применение при анализе сложного движения кулисного камня. Переносное движение осуществляет кулиса; относительное движение есть прямолинейное движение камня по направляющей кулисы (рис.2.4, б).

В частном случае, когда переносное движение поступательное, а относительное – вращательное, формулы (2.1) и (2.2) упрощаются. В силу свойств поступательного движения V_A = V_B, a_A' = a_B, кроме того a^K = 0, тогда

V_A= V_B + V_AB; (2.3)

a_A= a_B + a_AB.

Этот известный результат в теоретической механике формулируется так:

скорость точки равна геометрической сумме скорости полюса и скорости движения относительно полюса.

Аналогичные утверждения можно сделать и для ускорения.

Формулы (2.3) применяются только в том случае, когда можно указать полюс относительного вращательного движения. Например, в шарнирном четырехзвеннике (рис. 2.4, б) движение точки А можно рассматривать состоящим из движения полюса (точки В) и относительного движения точки А вокруг точки В.

2.4. Метод планов скоростей и ускорений.

План скоростей шарнирного четырехзвенника

Планом скоростей звена называется плоский пучок лучей, изображающих в масштабе абсолютные скорости точек звена; отрезки, соединяющие концы лучей, изображают относительные скорости точек. Совокупность планов скоростей звеньев с общим полюсом называется планом скоростей механизма.

Построим план скоростей шарнирного четырехзвенника (рис.2.5, а). Определим скорость точки А кривошипа по формуле V_A=ω₁L_OA. Выберем масштабный коэффициент плана скоростей k_V. и изобразим скорость точки А в масштабе лучом pa, проведенным из полюса p в направлении скорости точки А. Для определения скорости точки В запишем уравнение, аналогичное уравнению (2,3):

V_B =V_A + V_BA. (2.4)

В этом уравнении две неизвестные: величина скорости V_BA и величина скорости V_B. Такое векторное уравнение решается, т.к. оно эквивалентно двум скалярным уравнениям с двумя неизвестными. На рис.2.5 представлено графическое решение векторного уравнения (2.4). Полученное построение представляет план скоростей, т.к. соответствует приведенному выше определению.

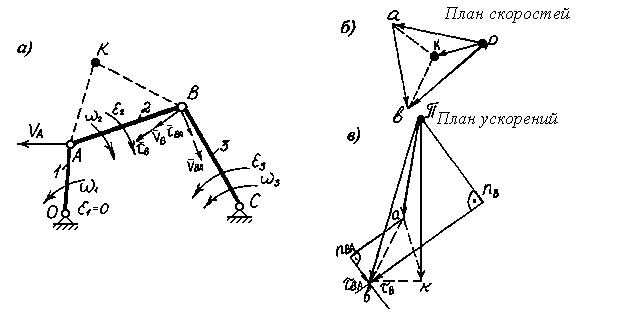
Рис.2.5. План скоростей и ускорений шарнирного четырехзвенника

План скоростей обладает рядом свойств:

1.Свойство подобия.

Фигура на плане скоростей, образованная векторами относительных скоростей, подобна и сходственно расположена по отношению к фигуре на звене, образованной соответствующими точками.

Если, например, на звене АВ находится точка К, то треугольник АВК должен быть подобен треугольнику авк на плане скоростей. Это свойство доказывается на основании того, что векторы относительных скоростей ав, ак и вк перпендикулярны отрезкам АВ, АК и ВК и , следовательно , треугольники авк и АВК имеют равные углы.

Сходственность расположения состоит в одинаковом порядке обхода вершин треугольников АВК и авк.

Свойство подобия позволяет найти скорость любой точки звена, если известны скорости двух точек этого звена. Для этого достаточно построить фигуру на плане скоростей подобную и сходственно расположенную по отношению к фигуре на звене.

2.По плану скоростей можно найти угловую скорость звена.

Для этого следует воспользоваться соотношениями, например, такого вида:

ω₂ = V_BA/L_BA = k_vba/L_BA.

Направление угловой скорости определится, если перенести вектор относительной скорости в соответствующую точку звена. Направление относительной скорости показывает направление угловой скорости.

2.5. План ускорений шарнирного четырехзвенника

Планом ускорений звена называется плоский пучок лучей, изображающих в масштабе абсолютные ускорения точек звена. Отрезки, соединяющие концы этих лучей , изображают относительные ускорения. Совокупность планов ускорений звеньев образуют план ускорений механизма.

Ускорение точки А складывается из касательного и нормального ускорений, определяемых по формулам a_Aⁿ = ω₁²L_OA и a_A^τ = ε₁L_OA. Из полюса π отложим отрезки n_A и τ_A, изображающие в масштабе a_Aⁿ и a_A^τ. Для точки В запишем уравнения

a_B=a_A+ a_BА ; (2.5)

a_Bⁿ+ a_B^τ= a_A+ a_BAⁿ+ a_BA^τ.

В этих уравнениях известны только величины касательных ускорений a_B^τ и a_BA^τ. Нормальные ускорения определяются по формулам a_Bⁿ = ω₃²L_BC, a_BAⁿ = ω₂²L_BA. Угловые скорости ω₃ и ω₂ находятся на основании построенного ранее плана скоростей. Из конца вектора τ_A откладывается вектор n_BA, а затем через его конец проводится линия направления вектора τ_BA. Из полюса π откладывается вектор n_B , и затем через его конец проводится линия направления вектора τ_B, Пересечение линий τ_BA и τ_B определит точку b. Выполненное построение является графическим решением векторного уравнения (2.5).

Свойства плана ускорений.

1. Свойство подобия .

Фигура на плане ускорений, образованная векторами относительных ускорений, подобна и сходственно расположена по отношению к фигуре на звене, образованной соответствующими точками.

Доказательство этого свойства основано на том, что относительные ускорения точек одного звена, а следовательно, и соответствующие отрезки на плане ускорений пропорциональны расстояниям между этими точками на звене. Треугольники с пропорциональными сторонами подобны. Свойство подобия позволяет по известным ускорениям двух точек звена найти ускорение любых других точек.

2. По плану ускорений можно найти угловое ускорение звена.

Для этого следует воспользоваться известными соотношениями между касательным и угловым ускорениями. Например, для звена 2

ε₂ = a_BA^τ/L_BA = k_aτ_BA/L_{BA .}

Для определения направления ε₂ следует перенести a_BA^τ в точку В. Направление касательного ускорения показывает направление углового ускорения.

Планы скоростей и ускорений кривошипно-ползунного механизма строятся аналогично, но несколько проще.

2.6. План скоростей и ускорений кулисного механизма

Построение плана скоростей кулисного механизма (рис.2.6) начинается со скорости точки А. Движение точки А можно рассматривать как сложное, происходящее за счет переносного вместе с кулисой 3 и относительного за счет движения камня по кулисе. Тогда справедливо следующее уравнение:

V_A=V_A′+ V_AA′, (2.6)

где A^′ - точка, принадлежащая переносной системе ,т.е. кулисе, лежащая под точкой A. В этом уравнении неизвестны величины векторов V_A и V_AA. Направление вектора V_A перпендикулярно кулисе, направление вектора V_AA′ - вдоль кулисы. Скорость точки D находится на основании свойства подобия, которое в данном случае выражается в пропорции

CD/CA = pd/pa, откуда pd = (CD/CA)pa.

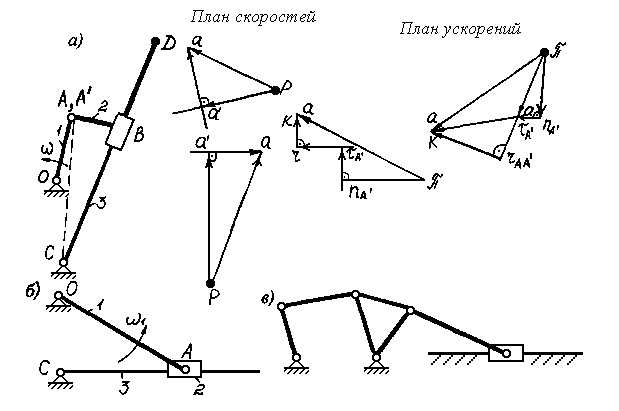
Рис.2.6. Планы скоростей и ускорений для кулисного механизма – а, кулисный механизм с вращающейся кулисой – б, рычажный механизм с двумя диадами – в

Для ускорения точки А в сложном движении следует записать уравнение:

a_A = a_A' + a_AA' + a^K = a_Aⁿ + a_A^τ+a_AA'+a^K .

В этом уравнении a_Aⁿ = ω₃²L_AC; a^к = 2ω₃V_AA.

Кроме того, известны направления всех векторов, неизвестны величины векторов a_A^τ, a_AA.

Построение плана ускорений производится в следующем порядке. Из полюса π откладывается вектор πa , изображающий ускорение точки А. Затем из полюса строится вектор n_A, а из его конца – линия направления вектора τ_A. Поскольку пока неизвестно , из какой точки следует строить вектор относительного ускорения r_AA , перейдем к построению кориолисова ускорения. Вектор k, изображающий a^K на плане ускорений, замыкает построение, приходя в точку а. Исходя из этого, находится начало вектора k. Через эту точку проводится линия направления вектора относительного ускорения. Пересечение линий r_AA и τ_A определяет точку a. План ускорений кулисного механизма построен.

Планы скоростей и ускорений кулисного механизма с вращающейся кулисой строятся подобным же образом (рис.2.6, б).

Многозвенные рычажные механизмы 2-го класса можно рассматривать как комбинации простейших четырехзвенных механизмов (рис.2.6, в). Поэтому приведенных примеров достаточно для графического исследования большинства применяемых механизмов.

Для уяснения содержания кинематической теоремы Кориолиса и усвоения приемов ее использования разберем ряд задач из курса ТММ.

Пример 1. Начнем с простейшего случая. Тело 1 совершает сложное плоское движение, двигаясь поступательно со скоростью ^r и ускорением ^r по прямолинейной направляющей (кулисе) 2, которая вращается относительно т. О с угловой скоростью . Нужно определить скорость и ускорение т. М и т. N, принадлежащих этому телу ( (Рис. 2.7).

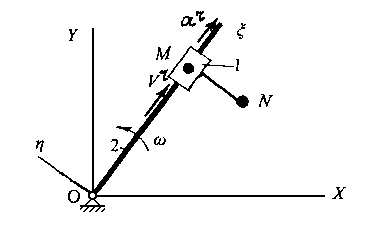
Рис. 2.7. Сложное движение движение кулисного камня

Выберем неподвижную систему координат xy и подвижную , связав ее с кулисой. Очевидно, что ускорение т. М и т. N определяются выражениями (2.7) и (2.8):

_m = _m’^e + _m^r + _m ^k ; (2.7)

_N = _N’^e + _N^r + _N . (2.8)

Правые части выражений (2.7) и (2.8) отличаются только переносными ускорениями _m’^e и _N’^e , т.к. т. М и т. N расположены в разных местах подвижной среды. Относительные ускорения и кориолисовы ускорения для т. М и т. N равны, т.к. в относительном движении тело движется поступательно, а угловая скорость переносного движения для обеих точек одна и та же.

_m^e=²ОМ,   _N^e=²ОN;

_m^k = _N^k = 2^r,   _m^r = _N^r.

Пример 2. Часто встречаются задачи, когда известно абсолютное ускорение, требуется определить переносное и относительное ускорения. Из выражения (2.7) получаем:

_m’^e = _m - _m^r - _m^k . (2.9)

Иногда это выражение записывают так:

_m’^e = _m + _m^r + _m^k. (2.10)

Очевидно, что в выражении (2.10) фигурируют не относительное и кориолисово ускорения, а векторы, равные им, но противоположные. Разъяснение этого обстоятельства в руководствах по ТММ часто отсутствует, что значительно затрудняет читателей.

Рассмотрим механизм на рис.2.8. Считаем, что абсолютное ускорение т. А задано.

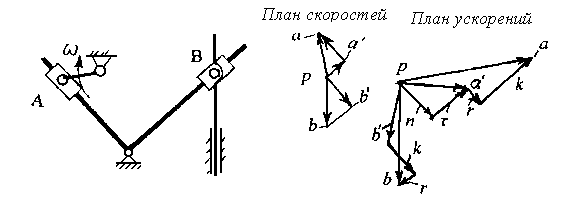
Рис. 2.8. Механизм с двумя кулисами и его план скоростей и план ускорений

Применив два раза теорему Кориолиса, имеем:

_А’^e = _А - _А^r - _А^k;

_В = _В’^e + _В^r + _В^k.

Уравнения решаются с помощью наложенных на движение звеньев связей.

Пример 3. Как показывает практика, наибольшие затруднения возникают при кинематическом анализе рычажных механизмов с поступательными парами. Рассмотрим несколько примеров таких «трудных» механизмов.

Механизмы по схемам а, б, в и г на Рис. 2.9 совершенно идентичны.

Затруднения возникают в связи с тем, что ищется «внутренняя» точка диады, как это рекомендуется в некоторых пособиях по ТММ. Такой точки для поступательной пары действительно нет. Точки, принадлежащие различным элементам поступательной пары, не являются общими, т.к. движутся по-разному. Такая точка имеется лишь во вращательной паре — это ее центр. Эта задача решается только через «внеш нюю» точку диады.

Из выражения для ускорения точки А в сложном движении следует:

_А’^e + _А^r = _А - _А^k.

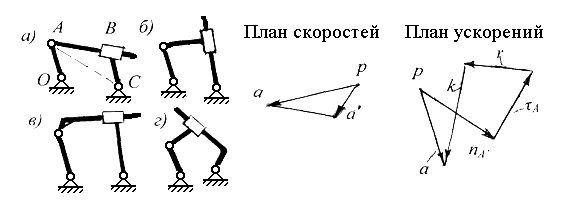
Рис. 2.9 Схемы механизмов с поступательными парами

В правой части уравнения записаны известные величины, в левой части — неизвестные. Уравнение решается, т.к. нормальная составляющая переносного ускорения т. А′ принадлежит переносной системе, связанной со звеном 3 и совпадающей в данный момент с т. А, определяется по величине (ⁿ = ²АС) и направлению. Касательная составляющая переносного ускорения ^ и относительное ускорение _А^r известны по направлению. На 2.9, е представлен векторный многоугольник, соответствующий записанному выше векторному уравнению.

На Рис.2.10 представлены частные случаи схем а и б Рис. 2.9. Здесь, помимо общего метода решения, можно применить еще частный метод. Рассмотрим схему на рис.2.9, а. Будем понимать под т. В элемент кинематической пары В, принадлежащий звену 2. Подчеркнем, что т. В не является «внутренней» точкой диады.

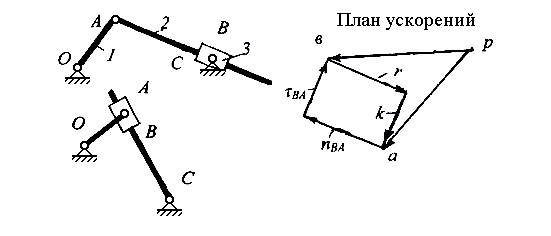
Рис. 2.10 Частные случаи кулисных механизмов

Запишем выражение для ускорения т. В в сложном движении, происходящем за счет участия во вращении со звеном 3 и движения относительно звена 3.

_В = _В’^e + _В^r + _В^k.

Здесь _В’^e = _С = 0. Именно благодаря этому условию возможно частное решение.

С другой стороны, сложное движение т. В можно рассматривать происходящим за счет участия в движении звена 1 и в движении относительно звена 1. Как будет показано в примере 5, выражение для ускорения т. В можно записать так:

_В = _А + _ВА.

Записанные уравнения образуют систему, решение которой представлено на рис. 2.10. Путь к решению оказался более долгим, чем в общем случае.

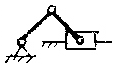
Пример 4. Механизмы по схемам а и б рис. 2.11, несмотря на внешние различия, идентичны.

Пусть нас интересует скорость и ускорение некоторой т. D. Запишем уравнения для определения скорости и ускорения т. D. Запишем уравнения для определения скорости и ускорения т. D в движении со звеном 1;

_Д = _Д1’^e + _Д1^r;

_Д = _Д1’^e + _Д1^r + _Д1^k.

Аналогичные уравнения можно записать относительно звена 3:

_Д = _Д3’^e + _Д3^r ;

_Д = _Д3’^e + _Д3^r + _Д3^k .

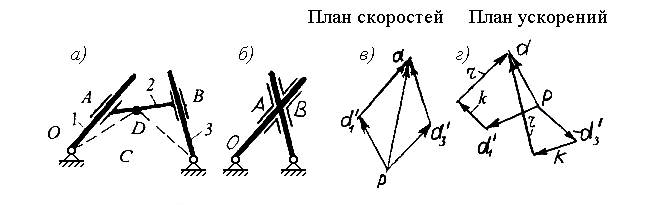
Рис. 2.11 Механизм крестовой муфты

Графическое решение системы уравнений приведено на Рис. 2.6g. При решении уравнений использовалось очевидное свойство механизма — звенья 1 и 2 движутся с одинаковыми скоростями и ускорениями. Благодаря этому свойству механизм применяется в качестве соединительной муфты, компенсирующей несоосность валов (муфта Ольдгейма или крестовая).

Пример 5. Специальным выбором подвижной системы координат можно упростить задачу, избавившись от кориолисова ускорения. Пусть т. М принадлежит звену 2 кинематической цепи, представленной на рис. 2.12 .

Рис. 2.12 Специальный выбор систем координат

Выберем неподвижную (xy) и подвижную () системы координат, как указано на схеме а рис.2.12. В таком случае ускорение т. М определяется обычным образом:

_М = _М’^e + _М^r + _М^k.

Здесь _М^r обусловлено вращением осей  с относительной угловой скоростью.

Выберем подвижные координаты по-другому: свяжем оси  со звеном 2 (схема б рис.2.12). Тогда т. М будет неподвижна в системе  и, следовательно, кориолисово и относительное ускорения отсутствуют:

_М = _М’^e.

Ускорение т. М равно ускорению той т. М^′ переносной системы, с которой в данный момент совпадает т. М. Как показано выше, переносное ускорение складывается геометрически из ускорения начала подвижных координат и ускорения, возникающего за счет вращения подвижных координат, с абсолютной угловой скоростью:

_М’^e = _А + _МА.

Можно выбрать подвижную систему координат еще одним специальным образом, связав ее начало с т. А и расположив оси  произвольным образом, но, требуя, чтобы этим осям было разрешено только поступательное движение (схема в рис. 2.12). Таким образом, оси  будут перемещаться по плоскости, все время оставаясь параллельными самим себе. Тогда скорость и ускорение любой точки М^′ , связанной с этими осями, будет равна скорости и ускорению т. А. В случае сложного движения т. М, обусловленного движением вместе с системой координат  и относительно ее, кориолисово ускорение отсутствует, т.к. переносное движение поступательное. Следовательно, полное ускорение складывается из переносного ускорения т. М^′ и относительного ускорения:

_М = _М’^e + _{МА =} _А + _МА.

Результат совпадает с предыдущим. Это не случайно. Полученный нами результат известен под названием теоремы Ривальса: «Ускорение произвольной точки твердого тела складывается из ускорения полюса и ускорения точки в ее движении относительно полюса».

В задачах ТММ, во всех тех случаях, когда относительное движение звена осуществляется посредством вращательной кинематической пары, возможно показанное выше упрощение. Для поступательной пары такое превращение невозможно, т.к. любая точка, которую можно признать за полюс, совершает сложное движение, а, следовательно, обладает кориолисовым ускорением.

Обобщая анализ приведенных примеров, можно придти к следующему выводу. При кинематическом анализе плоских четырехзвенных механизмов следует использовать кинематическую теорему Кориолиса. Из соответствующих уравнений для скорости и ускорения с учетом уравнений связей всегда можно найти параметры двух других движений, если задано третье движение. Так, если задано абсолютное движение, можно найти относительное и переносное, если задано относительное — то можно найти абсолютное и переносное, если задано переносное — абсолютное и относительное.

2.7. Метод кинематических диаграмм

Второй рассматриваемый графический метод – метод кинематических диаграмм, отличается простотой реализации, хорошо иллюстрирует связь между кинематическими параметрами , однако дает низкую точность результатов. Рассмотрим его на примере кривошипно-ползунного механизма (рис.2.13, а).

Положение точки В при заданном значении обобщенной координаты φ определяется координатой x. Если обозначить координату точки В в крайнем положении механизма x_o, то ее перемещение S_B = x - x_o. Перемещение представляет функцию угла φ. Задаваясь значениями этого угла, по планам положений механизма определим перемещения S и построим график S(φ). Поскольку φ = ωt, ось φ можно считать осью t и, следовательно, полученный график есть график S(t). Согласно определению скорости и графическому смыслу производной, имеем:

V = dS/dt = tgα_S k_V,

где α_S – угол наклона касательной к графику S(t). Отсюда следует способ построения графика V(t): проводятся касательные в выбранных точках графика S(t), измеряются углы наклона α_S, вычисляются тангенсы этих углов. Аналогичным образом находится ускорение:

a = dV/dt = tgα_V k_a.

Между графиками S(t), V(t), a(t) существует связь, как между интегральными и дифференциальными кривыми.

Рис. 2.13. Метод хорд: кинематическая схема механизма- а, метод графического дифференцирования – б, кинематические графики перемещений, скоростей и ускорений ползуна -в