2.4. Алгоритм возведения в степень

Рассматривается следующая задача: для заданного a (например, aR) и заданного n вычислить степень aⁿ.

Для примера рассмотрим вычисление a¹¹. Действуя «в лоб» последовательным умножением aaaaaaaaaaa, затратим 10 умножений. Действуя более изобретательно, можно получить результат всего за 5 умножений, а именно: 1) aa=a²; 2) (a²) (a²)=a⁴; 3) a⁴a=a⁵; 4) (a⁵) (a⁵) = a¹⁰; 5) a¹⁰a = a¹¹. Чтобы понять этот способ действий, рассмотрим естественное (рекурсивное) определение

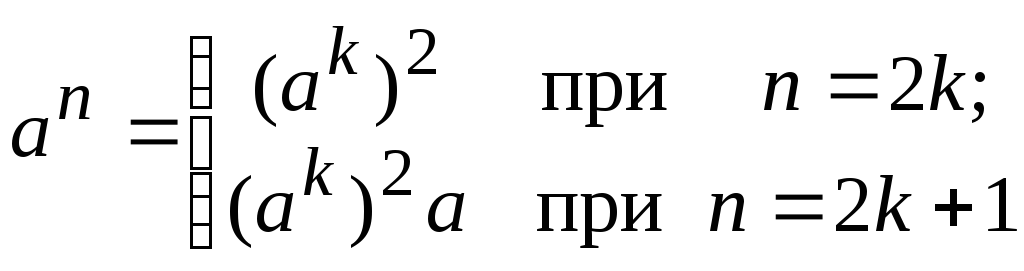(2.10)

и будем применять его последовательно. Например,

1) a¹¹ = (a⁵)² a, 2) a⁵ = (a²)² a, 3) a² = a  a.

Вычисления следует выполнять в обратном порядке: сначала вычислить a², затем a⁵ и, наконец, a¹¹.

Такой способ действий давно известен. Он называется «индийским» способом вычисления степени и впервые (около 200 года до н. э.) описан в древнем индийском трактате Чанда-сутра (исторические ссылки смотри у Д. Кнута в [2]).

Оказывается, что можно описать эти вычисления без ссылок на рекурсивное определение (2.10). Основную роль здесь будет играть двоичная система счисления. Рассмотрим двоичную запись показателя степени n, например: 11₁₀ = 1011₂. В этой последовательности нулей и единиц заменим каждый символ «0» на символ «К», а каждый символ «1» на пару символов «КУ». Для n = 1011₂ получим «КУККУКУ». Вычеркнем два первых слева символа «КУ» (они соответствуют первому слева символу «1» в двоичной записи). Для n = 1011₂ получим «ККУКУ». Установим текущий результат равным a. Далее читаем полученную последовательность слева направо и выполняем следующие действия: если встретился символ «У», то умножаем текущее значение на a, если же очередной символ есть «К», то возводим текущее значение в квадрат. Для нашего примера при n = 1011₂ получим:

0. b := a; { b = a}

1. {К} b := sqr(b); { b = a²}

2. {КУ} b := sqr(b); b := b*a; { b = a⁵}

3. {КУ} b := sqr(b); b := b*a; { b = a¹¹}.

В общем случае обосновать эти действия можно следующим образом. Пусть вычислено b = a^m. Рассмотрим число M = 2m + , где  = 0 или 1. Переход от числа m к числу M соответствует приписыванию справа к двоичной записи числа m одного бита . Тогда имеем a^M = a^2m +  = (a^m)²a^. При  = 0 получаем a^M = (a^m)², что соответствует операции «К», а при  = 1 получаем a^M = (a^m)²a, что соответствует операции «КУ». Вся последовательность действий получается в результате чтения двоичной записи показателя степени n слева направо и обработки очередного бита  указанным ранее способом. Подсчитаем общее количество умножений, выполняемых при «индийском» способе. Длина двоичной записи числа n равна log₂ n + 1. Пусть N1(n) есть число единиц в двоичной записи числа n. Тогда общее количество операций умножения и возведения в квадрат (с учётом отбрасывания первых символов «КУ») будет log₂ n + 1 + N1(n)  2 или log₂ n + N1(n)  1.

Рассмотренный алгоритм можно назвать бинарным методом «слева направо». Для компьютерной реализации более эффективным оказывается аналогичный бинарный алгоритм, основанный на анализе двоичной записи показателя степени справа налево. Опишем процесс разработки этого алгоритма, основанный на конструктивном использовании понятия инварианта цикла.

Для начала рассмотрим более простую вспомогательную задачу вычисления по заданному n функции N1(n)  числа единиц в двоичной записи числа n. Приведём примеры: N1(11₁₀) = N1(1011₂) = 3, N1(32₁₀) = N1(100000₂) = 1, N1(31₁₀) = N1(11111₂) = 5.

Анализ двоичной записи числа n справа налево выполним, используя булевскую функцию Odd(n): если справедливо Odd(n), т. е. n нечётно, то последний (крайний справа) бит в двоичной записи n есть 1; если же справедливо not Odd(n), т. е. n чётно, то последний бит в двоичной записи n есть 0. Переход к следующему слева биту осуществляется операцией n div 2. Пусть выполнено i таких шагов (0 < i < log₂ n + 1). Для анализируемой части двоичной записи значения переменной n введем переменную m, сохраняя n неизменной. Состояние после i-го шага схематически изображено на рис. 2.1.

				i	i 1		…	2	1	0	Показатели степени двойки
		…					…				Двоичная запись n ({0,1})
				i+1	i	i 1	…	3	2	1	Номера разрядов (шаги)
							
Двоичная запись m					Двоичная запись p

Рис. 2.1. Состояние после i-го шага

Здесь p – число, двоичную запись которого составляют правые i бит двоичной записи числа n. Очевидно, что N1(n) = N1(m) + N1(p). Например, при n = 86₁₀ = 1010110₂ и i = 4 имеем m = 101₂ = 5₁₀ и N1(m) = 2, а также p = 110₂ = 6₁₀ и N1(p) = 2. Поскольку N1(n) = 4, то действительно N1(n) = N1(m) + N1(p) = 2 + 2 = 4. Рис. 2.2 иллюстрирует этот факт.

7	6	5	4	3	2	1	0	Показатели степени двойки
0	1	0	1	0	1	1	0	Двоичная запись n
8	7	6	5	4	3	2	1	Номера разрядов (шаги)
				
Двоичная запись m				Двоичная запись p

Рис. 2.2. Иллюстрация соотношения N1(n) =N1(m) + N1(p)

Пусть в цикле просмотра двоичной записи справа налево вычисляется y = N1(p), тогда в качестве инварианта цикла рассмотрим соотношение N1(n) = N1(m) + y, и вместе с условием окончания цикла m = 0 оно даст требуемое постусловие N1(n) = y. Программа, вычисляющая функцию N1(n) , имеет следующий вид:

{n0}

m := n; y :=0;

{Инвариант: (N1(n) = N1(m) + y) & (0  m  n) }

while m > 0 do

begin

if Odd(m) then y := y + 1;

m := m div 2;

end;

{y=N1(n)}

Вернёмся к задаче вычисления степени. Основной цикл и в этой задаче будет соответствовать просмотру двоичной записи n справа налево. Представляет интерес инвариантное утверждение, описывающее состояние программы (связь между переменными программы) на произвольном шаге этого цикла. Из рис. 2.1 ясно, что после i-го шага n = m 2ⁱ + p. Для примера с n = 86₁₀ = 1010110₂ и i = 4 (рис. 2.2) действительно имеем 86₁₀ = 5 2⁴ + 6. Тогда для степени aⁿ после i-го шага имеем представление

. (2.11)

Предположим, что в цикле кроме m вычисляются ещё две величины Тогда из (2.11) получимaⁿ = b^m c. Это и будет инвариант цикла. Более точно инвариантом будет (aⁿ = b^m c) & (0  m  n). Если перед началом цикла положить m = n, c = 1 и b = a, то инвариант перед циклом будет выполнен. Таким образом, можно записать набросок цикла:

{Предусловие: n>0}

m := n; c := 1; b := a;

{Инвариант: (aⁿ = b^m c) & (0  m  n)}

while m > 0 do

begin

ТЕЛО ЦИКЛА

end;

{Постусловие: ?}

Уже известно (см. задачу вычисления N1(n)), как изменяется переменная m в теле цикла: переход к следующему биту двоичного представления реализуется операцией m div 2. Тогда после завершения цикла получим m = 0 и из инварианта будет следовать aⁿ = b^m c = b⁰ c = с. Таким образом, постусловием этого цикла является с = aⁿ, т. е. требуемый результат сформируется в переменной c.

Используя инвариант цикла, определим остальные операции в теле цикла. Пусть

ТЕЛО ЦИКЛА: {(aⁿ = b^m c) & (0 < m  n)}

Операторы изменения переменных b и c;

m := m div 2;

{(aⁿ = b^m c) & (0  m  n)}

По правилу вывода для оператора присваивания (2.3) имеем следующее свойство оператора m := m div 2 :

{(aⁿ = b^{m div 2} c) & (0  (m div 2)  n)} m := m div 2 {(aⁿ = b^m c) & (0  m  n)}

или с учётом следования (0 < m  n)  (0  (m div 2)  n) получаем

{(aⁿ = b^{m div 2} c) & (0 < m  n)} m := m div 2 {(aⁿ = b^m c) & (0  m  n)}.

Тогда для того чтобы тело цикла обладало сформулированным ранее свойством, первая часть тела цикла «Операторы изменения переменных b и c» должна обладать свойством

{(aⁿ = b^m c) & (0 < m  n)}

Операторы изменения переменных b и c;

{(aⁿ = b^{m div 2} c) & (0 < m  n)}.

Рассмотрим отдельно случаи чётного и нечётного значения m. Пусть not Odd(m), тогда m = (m div 2) 2 и требуемое свойство

{aⁿ = b^{(m div 2) 2} c}

Операторы изменения переменных b и c;

{aⁿ = b^{m div 2} c}

можно обеспечить, используя оператор b := sqr(b). Действительно, слабейшее предусловие для оператора присваивания b := sqr(b) относительно постусловия aⁿ = b^{m div 2} c есть aⁿ = (b²)^m div 2 c = b^{(m div 2) 2} c, что совпадает с требуемым предусловием тела цикла.

Пусть теперь Odd(m), тогда m = (m div 2) 2 + 1 и требуемое свойство

{aⁿ = b^{(m div 2) 2 +1} c}

Операторы изменения переменных b и c;

{aⁿ = b^{m div 2} c}

можно обеспечить, используя кроме оператора b := sqr(b) ещё и добавленный перед ним оператор c := c*b. Действительно, слабейшее предусловие для пары операторов c := c*b и b := sqr(b) относительно постусловия aⁿ = b^m div 2 c есть aⁿ = (b²)^m div 2 (c*b) = b^{(m div 2) 2 +1} c, что совпадает с требуемым предусловием тела цикла.

Таким образом, программа вычисления степени принимает законченный вид

{Предусловие: n>0}

m := n; c := 1; b := a;

{Инвариант: (aⁿ = b^m c) & (0  m  n)}

while m > 0 do

begin

if Odd(m) then c := c*b;

b := sqr(b);

m := m div 2;

end;

{Постусловие: c = aⁿ}

Проследим за работой этого алгоритма при n = 11. В каждой строке табл. 2.1 приведены значения переменных программы после завершения соответствующего шага. Установка начальных значений (инициализация цикла) обозначена как 0-й шаг. В последнем столбце указан инвариант цикла aⁿ = b^mc, причём вместо b и c подставлены их текущие (полученные после данного шага) значения.

Таблица 2.1

Номер шага	Десятичная запись m	Двоичная запись m	b	c	Примечание
0	1110	10112	a	1	a11= (a)111
1	510	1012	a2	a	a11= (a2)5a
2	210	102	a4	a3	a11= (a4)2a3
3	110	12	a8	a3	a11= (a8)1a3
4	010	02	a16	a11	a11= (a16)0a11

Общее количество умножений (по шагам) есть 2 + 2 + 1 + 2 = 7. Для этого же значения n = 1011₂ «индийский» способ даёт последовательность «[КУ]ККУКУ» и соответственно число умножений, равное 5, что на два умножения меньше, чем в полученном бинарном алгоритме «справа налево». Эти два «лишних» умножения производятся по одному на первом и на последнем шагах алгоритма. На последнем шаге происходит лишнее (впрок для следующего шага) возведение в квадрат, от которого можно избавиться (см. далее модификацию этого алгоритма). «Лишнее» умножение 1a на первом шаге выполняется в операторе c := c*b при начальных значениях c = 1 и b = a. Важно, что это «лишнее» умножение не всегда будет производиться на первом шаге, как показывает пример с n = 12 (табл. 2.2).

Таблица 2.2

Номер шага	Десятичная запись m	Двоичная запись m	b	c	Примечание
0	1210	11002	a	1	a12= (a)121
1	610	1102	a2	1	a12= (a2)61
2	310	112	a4	1	a12= (a4)31
3	110	12	a8	a4	a12= (a8)1a4
4	010	02	a16	a12	a12= (a16)0a12

Это умножение (первое выполнение оператора c := c*b) производится тогда, когда при сканировании двоичной записи n справа налево в первый раз встретится «1».

В общем случае этот способ требует выполнения log₂ n + N1(n) + 1 умножений. Лишнее умножение на последнем шаге алгоритма (при m = 1) можно исключить, завершая цикл при m = 1 и выполняя в последний раз оператор c := c*b уже вне цикла. Это даст число умножений, равное log₂ n + N1(n). Такого же результата можно достигнуть более элегантным способом в следующей модификации алгоритма.

Ещё раз обратимся к телу цикла и его предполагаемому свойству. Оказывается, что прежняя конструкция тела цикла не единственна. Рассмотрим отдельно случай чётного и нечётного значений m. При чётных m, как было установлено ранее, операции m := m div 2 и b := sqr(b) сохраняют инвариант. Заметим, что новое значение m может быть как чётным, так и нечётным. Пусть m – нечётное, тогда инвариант цикла можно сохранить, используя операции m := m  1 и c := c*b. При этом новое значение m заведомо чётно. Данные соображения наводят на мысль о выделении внутреннего цикла (после выполнения которого сохранён инвариант объемлющего цикла):

{ not Odd(m), возможно, кроме первого входа}

while not Odd(m) do begin m := m div 2; b := sqr(b) end;

{Odd(m)}

На выходе из цикла будет Odd(m), поэтому можно выполнить рассмотренные ранее для этого случая действия m := m  1 и c := c*b, сохраняющие инвариант. Комбинируя эти два фрагмента, получим новое тело цикла и, соответственно, новый вариант алгоритма:

{Предусловие: n >0}

m := n; c := 1; b := a;

{Инвариант: (aⁿ = b^m c) & (0  m  n)}

while m > 0 do

begin

{ not Odd(m), возможно, кроме первого входа}

while not Odd(m) do begin m := m div 2; b := sqr(b) end;

{Odd(m)}

m := m  1; c := c*b { not Odd(m) }

end;

{Постусловие: c = aⁿ}

Рассмотрим примеры работы этой версии алгоритма при n = 11 и n = 12.

Пример: n = 11. Работа алгоритма отражена в табл. 2.3. Здесь на каждом выделенном в строку таблицы шаге, производится либо возведение в квадрат, либо умножение. Всего таких действий 6.

Пример: n = 12. Работа алгоритма отражена в табл. 2.4. Здесь использовано 5 умножений.

В общем случае эта версия требует log₂ n + N1(n) умножений.

Рассмотренный метод вычисления степеней хороший (существенно лучше, чем последовательные умножения), но не оптимальный. Например, при n = 15₁₀ = 1111₂ бинарный метод справа налево требует выполнения 7

Таблица 2.3

Номер шага	Номер шага внешнего цикла	Номер шага внутреннего цикла	Десятичная запись m	Двоичная запись m	b	c
0	0	0	1110	10112	a	1
1	1	-	1010	10102	a	a
2	2	1	510	1012	a2	a
3	2	-	410	1002	a2	a3
4	3	1	210	102	a4	a3
5	3	2	110	12	a8	a3
6	3	-	010	02	a8	a11

Таблица 2.4

Номер шага	Номер шага внешнего цикла	Номер шага внутреннего цикла	Десятичная запись m	Двоичная запись m	b	c
0	0	0	1210	11002	a	1
1	1	1	610	1102	a2	1
2	1	2	310	112	a4	1
3	1	-	210	102	a4	a4
4	2	1	110	12	a8	a4
5	2	-	010	02	a8	a12

умножений, а бинарный метод слева направо («индийский») – 6 умножений. Оказывается можно вычислить a¹⁵ всего за 5 умножений: 1) a  a = a²; 2) a²  a² = a⁴; 3) a⁴  a = a⁵; 4) a⁵  a⁵ = a¹⁰; 5) a¹⁰  a⁵ = a¹⁵. Описание оптимального метода можно найти в [2].