Разбор типовых примеров

Пример 1. Найти все решения уравнения:

а) б)

в) г)

Решение. а) Сначала решим однородное уравнение. Его характеристическое уравнение: Корни: Поэтому Имеем: поэтому Далее, (степень многочлена (так как не является корнем характеристического уравнения). Поэтому частное решение неоднородного уравнения следует искать в виде т.е. Продифференцируем эту функцию: Подставим в исходное уравнение: Приравняв коэффициенты при и свободные члены в левой и правой частях равенства, получим: Отсюда Таким образом, частное решение неоднородного уравнения равно Прибавив к этому решению все решения однородного уравнения, получим ответ:

б) Найдём общее решение однородного уравнения. Характеристическое уравнение: Его корни: Значит, Будем искать частные решения уравнений:

Пусть сначала Тогда Значит, Подставим в уравнение Следовательно,

Пусть теперь Тогда поэтому Отсюда следует вид частного решения уравнения: Имеем:

Подставим в уравнение

Отсюда: Таким образом,

Наконец, рассмотрим уравнение Здесь поэтому Имеем: Подставим в уравнение Отсюда получаем систему: 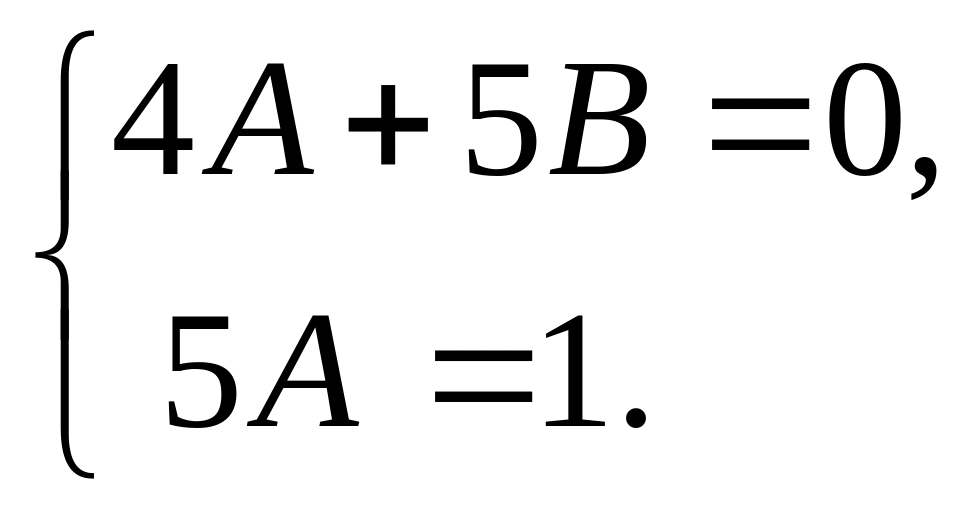Решение системы: Следовательно,

Так как то окончательный ответ выглядит так:

в) Решаем однородное уравнение Его характеристическое уравнение: Отсюда Поэтому Неоднородное уравнение разобьём на два: и

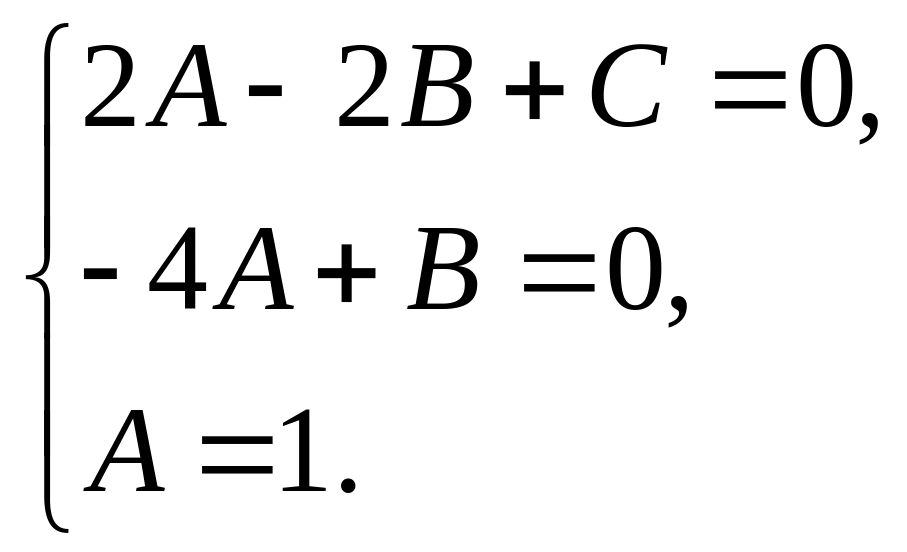Для уравнения имеем: поэтому Продифференцируем: Подставим в уравнение Приравнивая коэффициенты при получим систему Её решение: Следовательно,

Для уравнения Поэтому Дифференцируем: Подставляем в уравнение

Упростим: Отсюда Следовательно, Прибавив к сумме общее решение однородного уравнения, получим ответ:

г) Решим однородное уравнение Его характеристическое уравнение: Корни: Следовательно, Здесь поэтому Так как то Так как не является корнем характеристического уравнения, то Таким образом, частное решение неоднородного уравнения следует искать в виде

Дифференцируем:

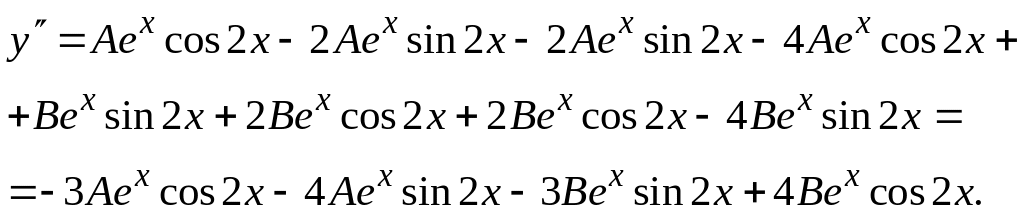
Подставим в исходное уравнение:

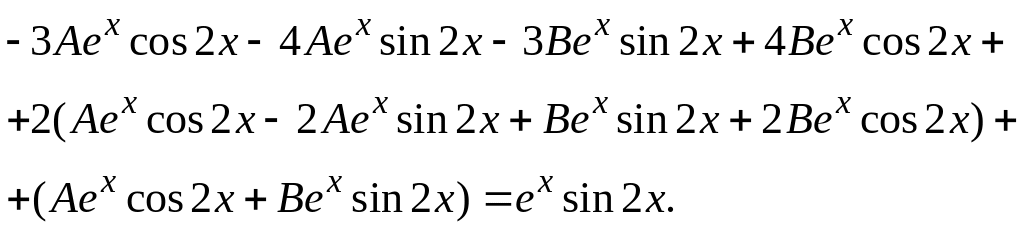
После упрощения получим: Отсюда Таким образом, Прибавив к этой функции общее решение однородного уравнения, получим ответ:

Пример 2. Написать вид частного решения неоднородного уравнения с неопределёнными коэффициентами, при этом коэффициенты не находить:

а)

б) в)

Решение. а) Характеристическое уравнение однородного уравнения: Его корни: В правой части уравнения стоят функции

Для функции имеем: Поэтому

Для функции имеем: Поэтому

Для функции имеем: Поэтому

Таким образом,

б) Характеристическое уравнение однородного уравнения имеет вид откуда Имеем: Следовательно,

в) Характеристическое уравнение однородного уравнения: т.е. Его корни:

Для уравнения имеем: поэтому

Для уравнения имеем: поэтому

Таким образом,

Пример 3. Решить систему:

а) 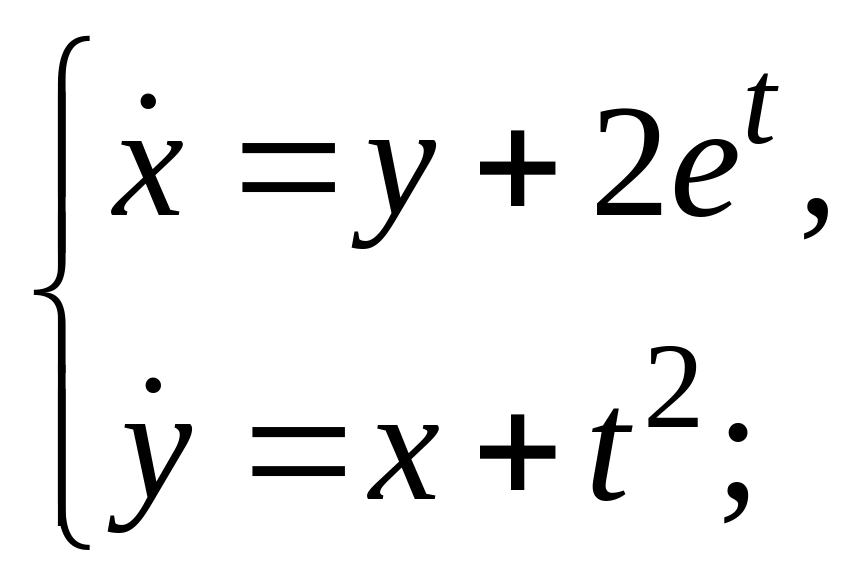б)

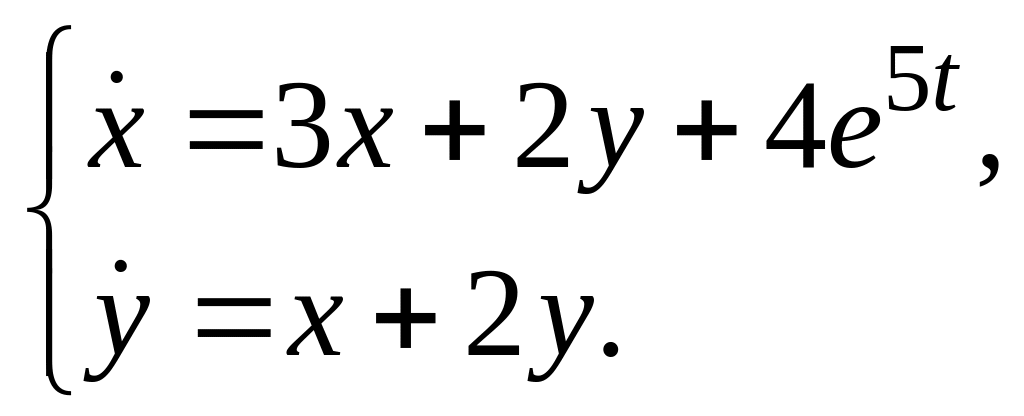
Решение. Запишем систему в матричном виде: 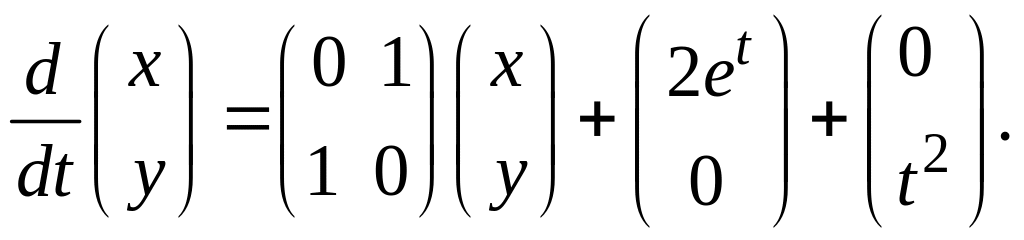Характеристическое уравнение однородной системы имеет вид 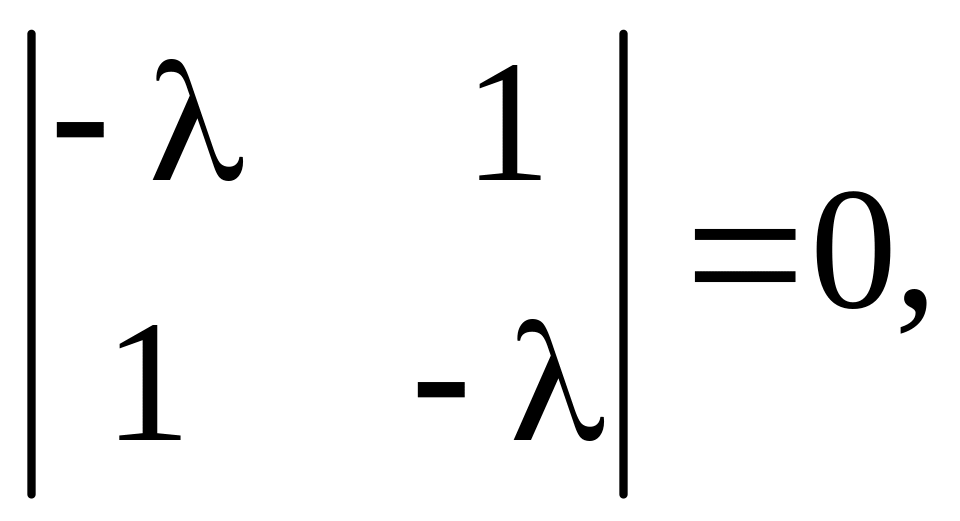т.е. Его корни: Составим систему алгебраических уравнений для нахождения собственных векторов.

Для имеем систему 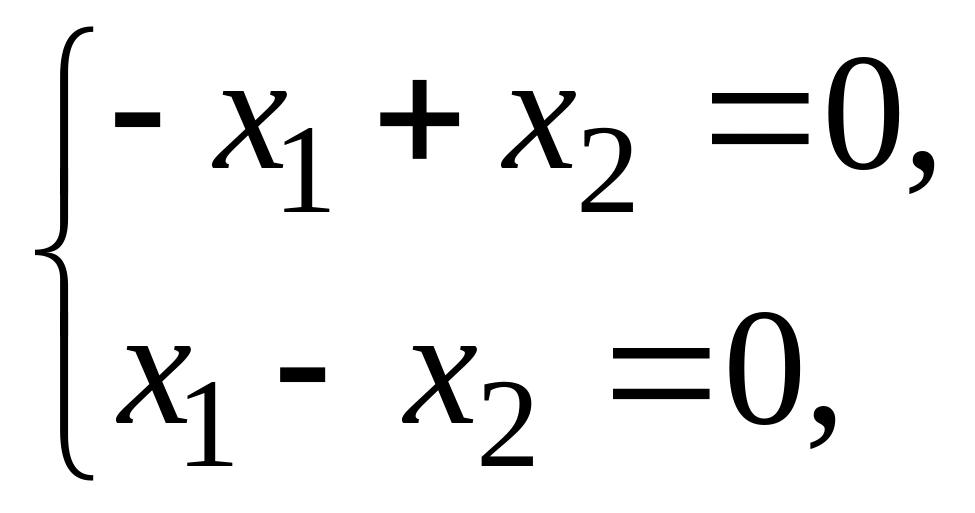откуда получаем собственный вектор

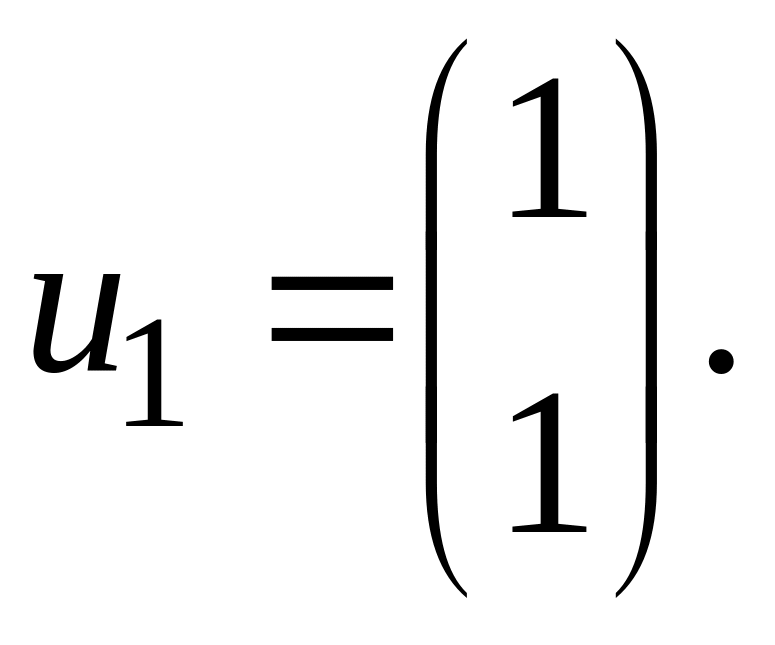
Для имеем систему 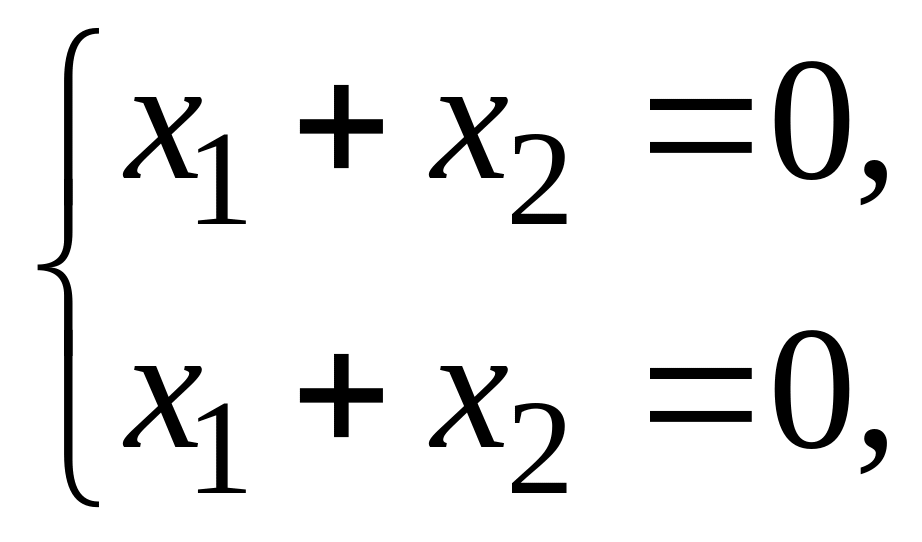откуда

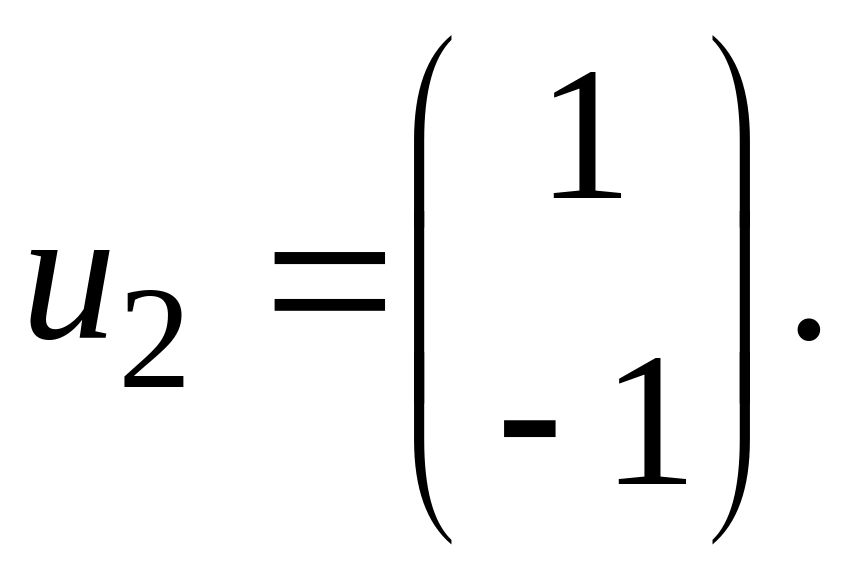
Значит,

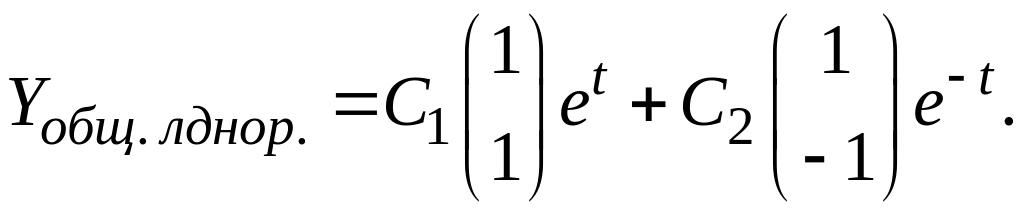
Перейдём к решению неоднородной системы. Её разобьём на две системы.

Для системы 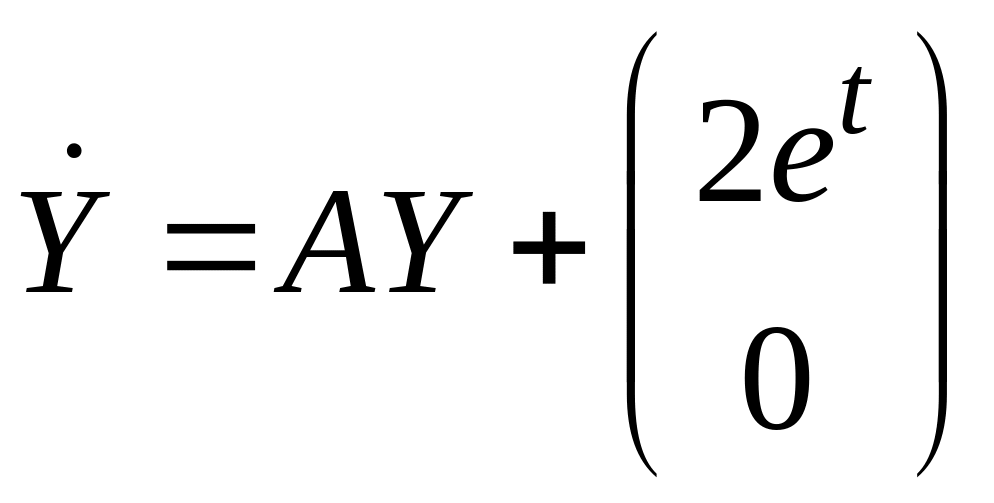имеем: поэтому 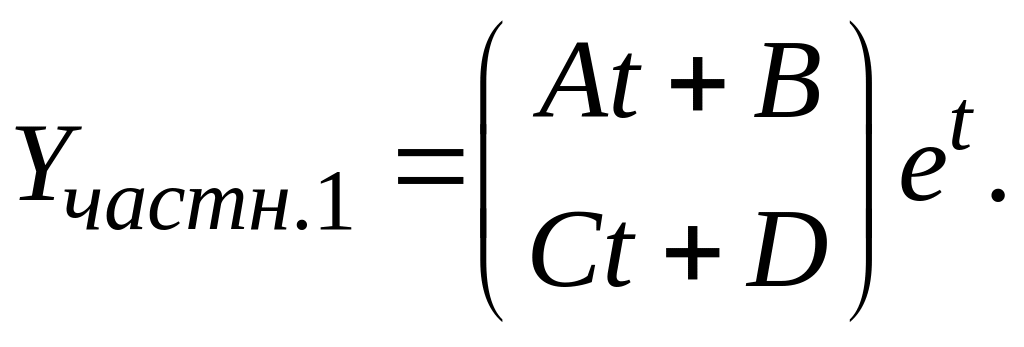Продифференцируем эту вектор-функцию: 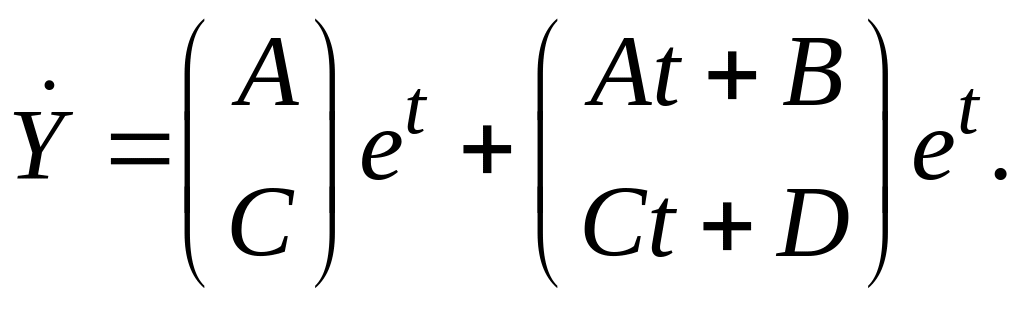Подставим в систему

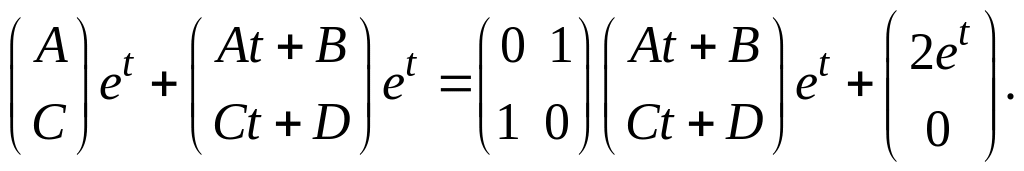
Упростим: 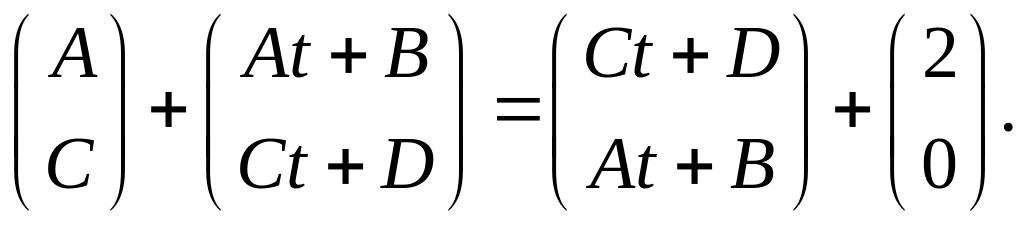Приравнивая коэффициенты многочленов в правой и левой частях равенства, получим:

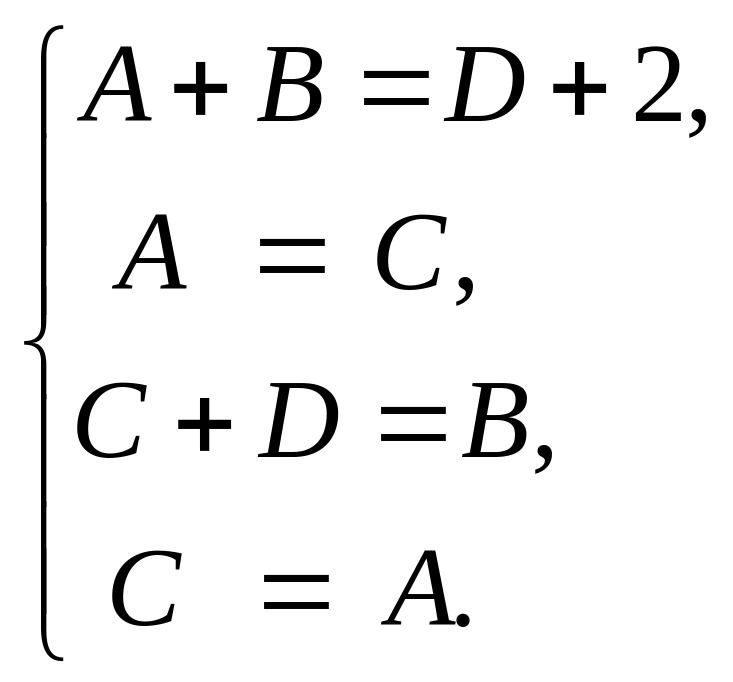
Решением этой системы служит, например, следующий набор чисел: Следовательно,

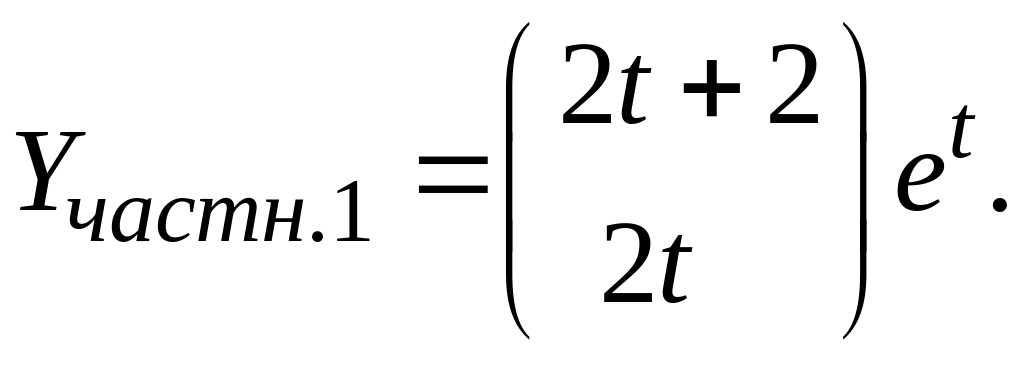
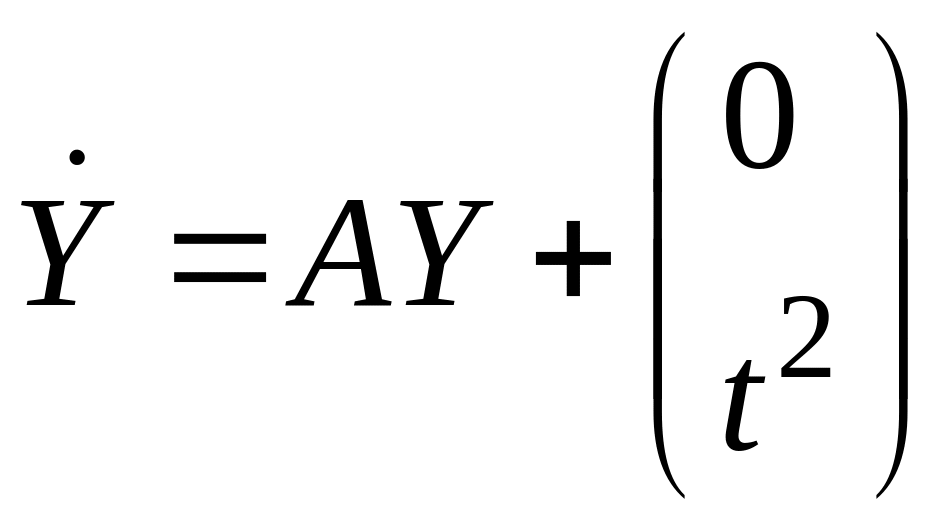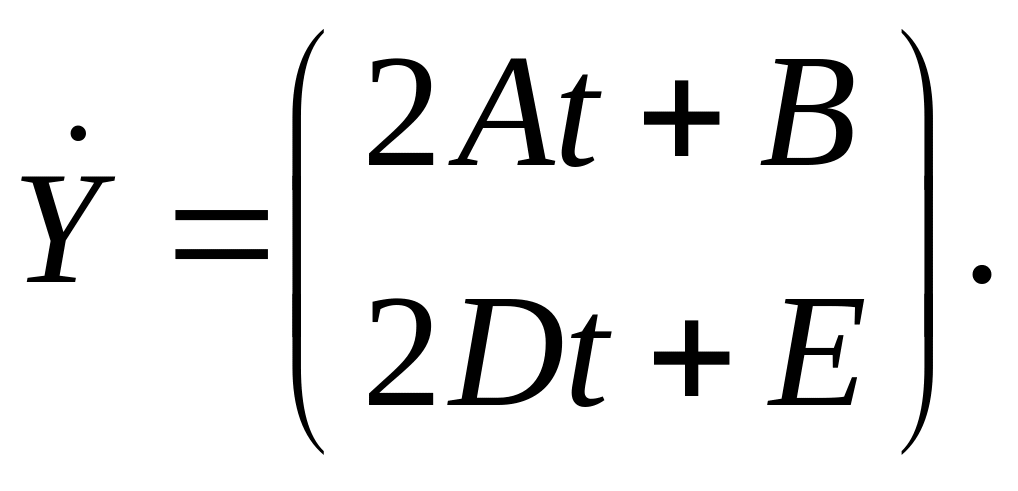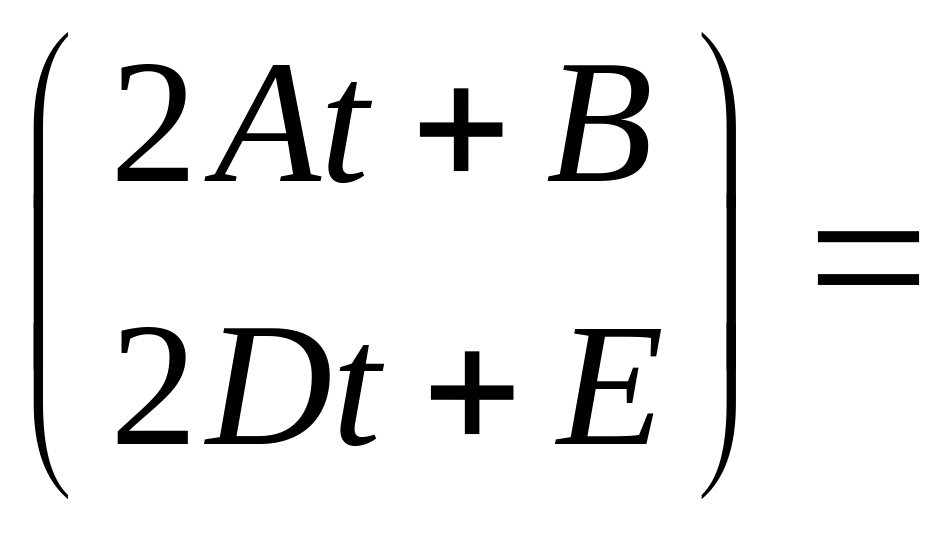
Для системы имеем: поэтому Продифференцируем: Подставим в систему 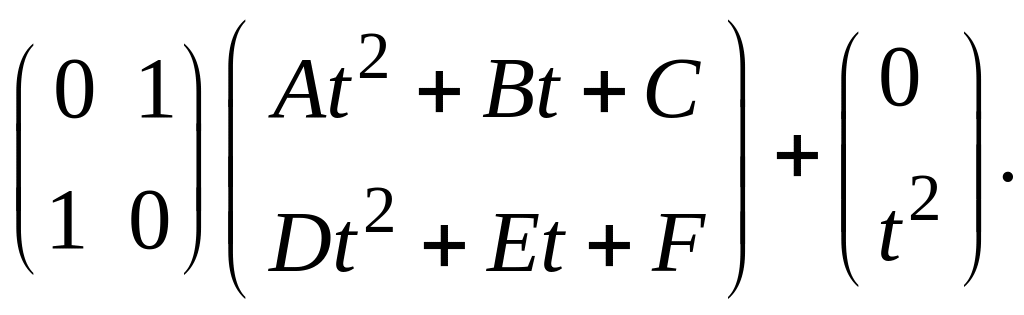Отсюда следует, что

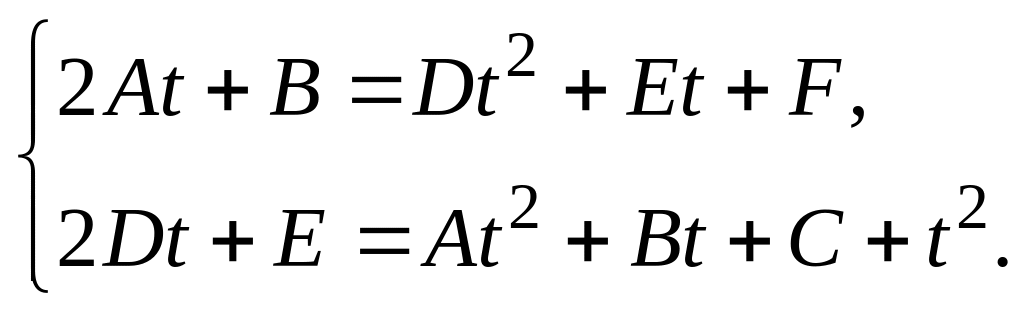
Для коэффициентов получается система линейных алгебраических уравнений: Решение системы: Следовательно, 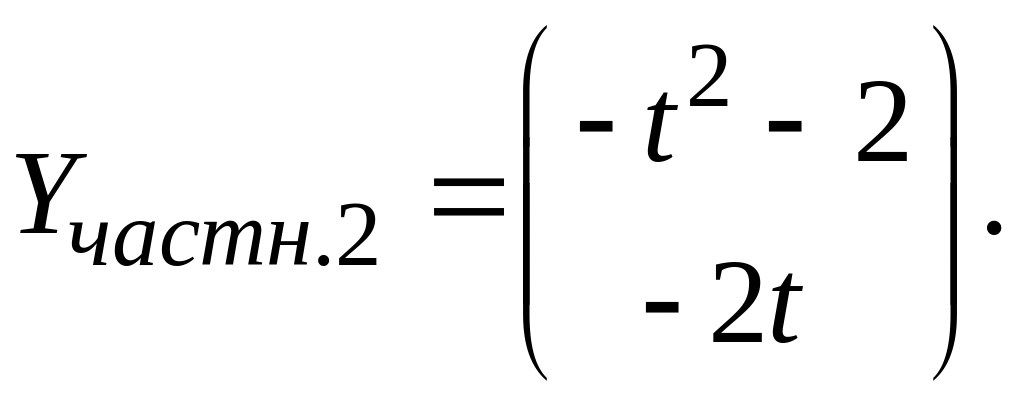Складывая частные решения с общим решением однородной системы, получим ответ:

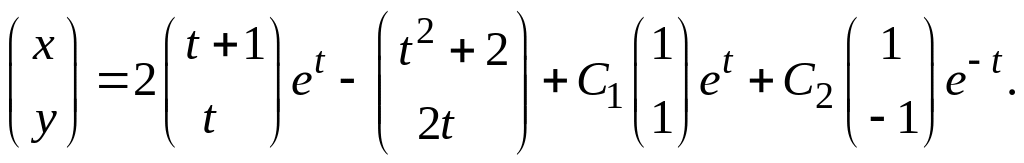
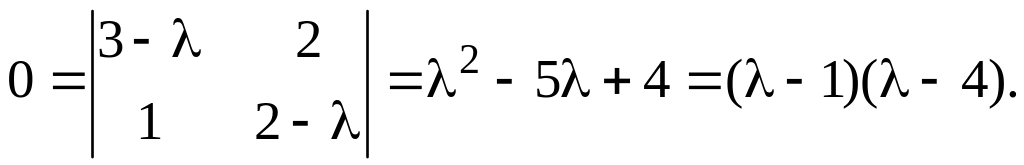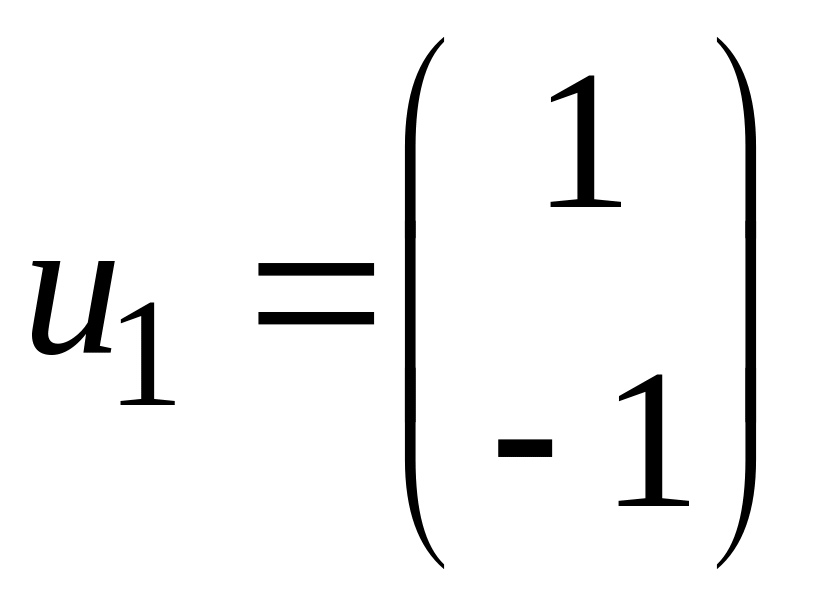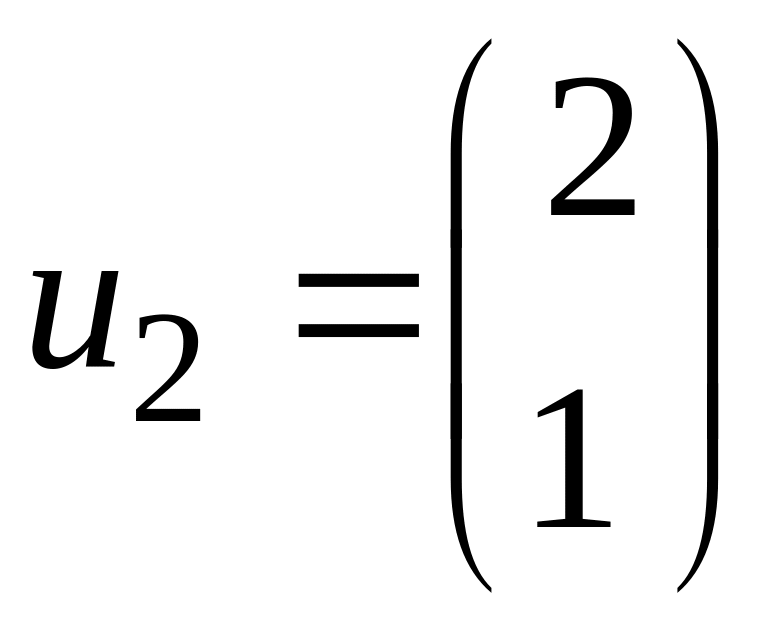(б) Вначале решим однородную систему Характеристическое уравнение: Его корни: Собственные векторы: для для Общее решение однородной системы: 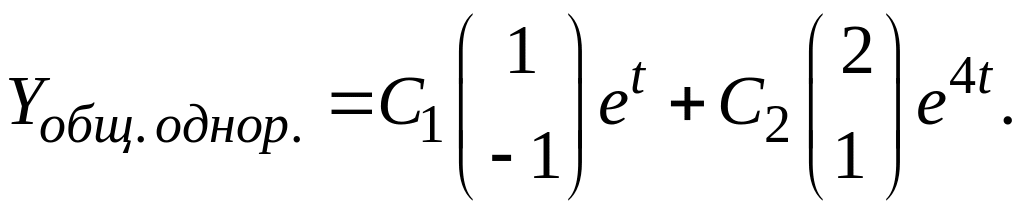Перейдём к решению неоднородной системы. Имеем: Поэтому частное решение неоднородной системы следует искать в виде 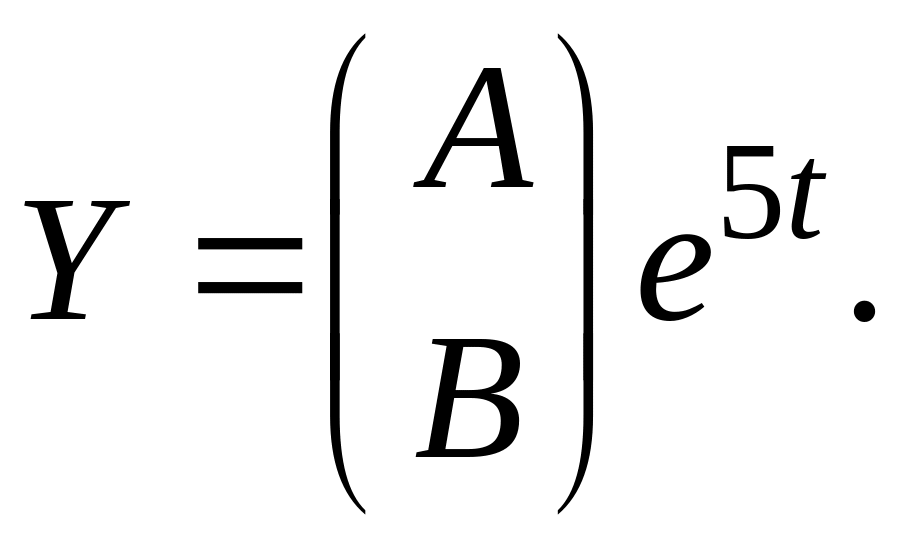Подставим в неоднородную систему: 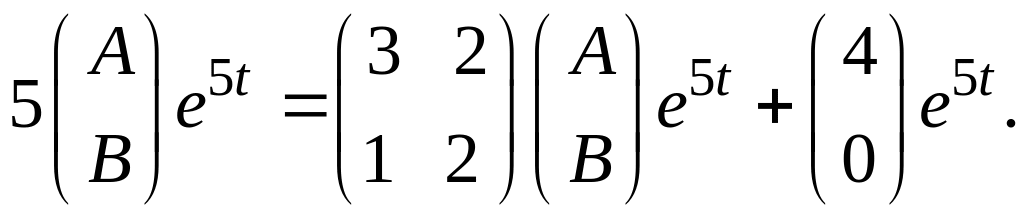Отсюда получаем систему линейных алгебраических уравнений: Её решение: Значит, 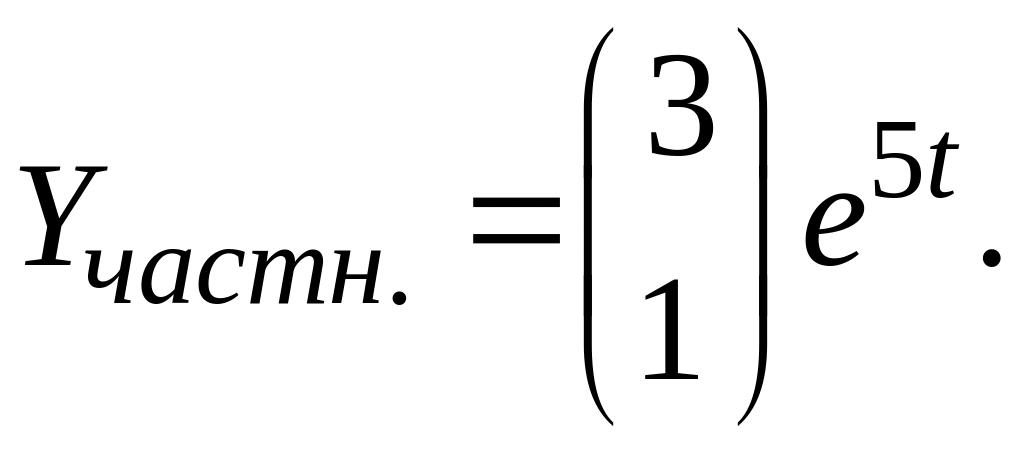Таким образом, общее решение системы имеет вид

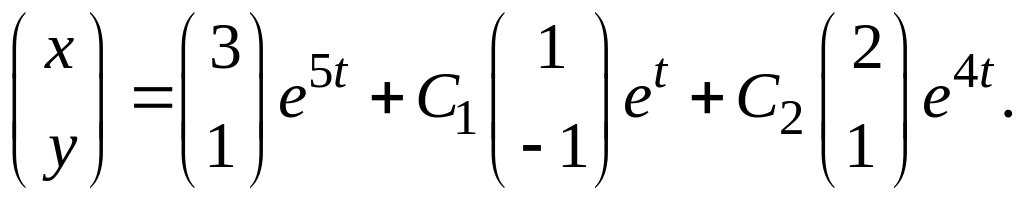
Пример 4. Решить интегральное уравнение

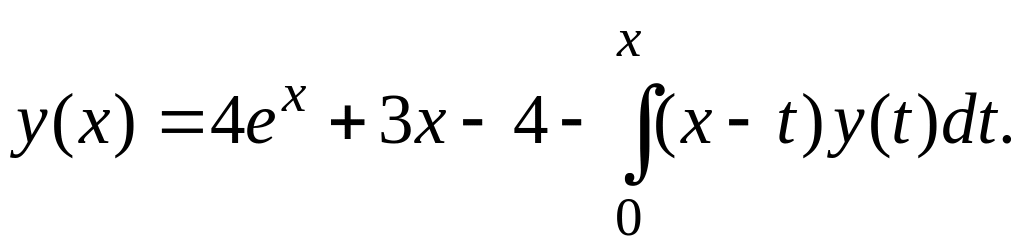
Решение. Продифференцируем уравнение

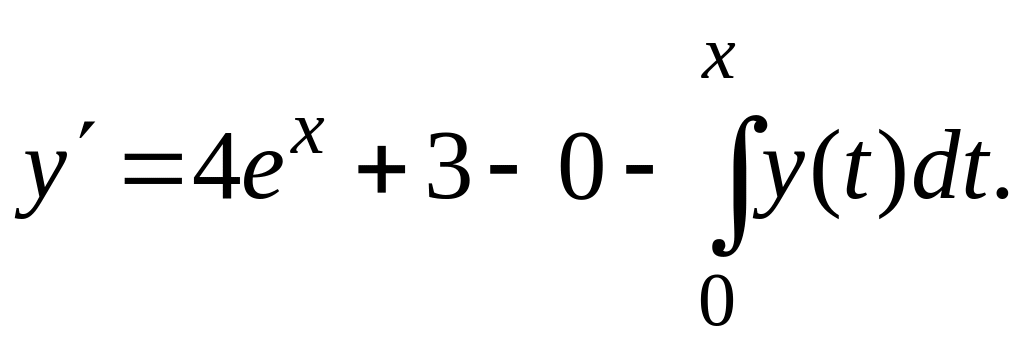
Продифференцируем ещё раз:

Решение однородного уравнения имеет вид Частное решение однородного уравнения ищем в виде После подстановки в уравнение находим коэффициент Оказывается, что Следовательно, общее решение уравнения имеет вид

Продифференцируем это равенство:

Из равенства получаем: Подставим в равенство Отсюда Из уравнения при получаем: Подставим в равенство Следовательно, Подставив найденные значения в равенство получим окончательный ответ: